Раздел 4. Математический анализ. Функции нескольких переменных

4.1 Понятие функции нескольких переменных

Функции двух переменных

Пусть на плоскости ХОУ имеется некоторое множество точек D и каждой точке поставлено в соответствие по некоторому правилу число. Тогда говорят, что на множествеD задана функция . Аргументом этой функции служит точка Р, пробегающая множествоD, а значением – величина (переменная) z. Положение каждой точки Р определяется парой ее координат и:. Координаты этой точки независимы друг от друга и поэтому можно сказать, что задана функция.

Определение. Переменная величина называется функцией двух независимых переменныхи, заданной на некотором множествеD, если по некоторому закону или правилу каждой паре соответствует определенное значение.

Пример. Пусть и- длины сторон прямоугольника,- его площадь. Тогда- функция двух независимых переменныхи, заданная на множестве.

Пусть функция определена в некоторой областиD, а точка - либо точка этой области, либо граничная дляD, в самой точке функция может быть не определена.

Определение. Число есть предел функциипри, если для любогонайдетсятакое, что во всех точках Р областиD, попавших в - окрестность точки, выполняется неравенство:

.

Пусть задана в областиD и - внутренняя точка областиD. Дадим аргументам иприращенияи. Тогда- полное приращение функции в точке.

Условие непрерывности в точкеможно записать так:

.

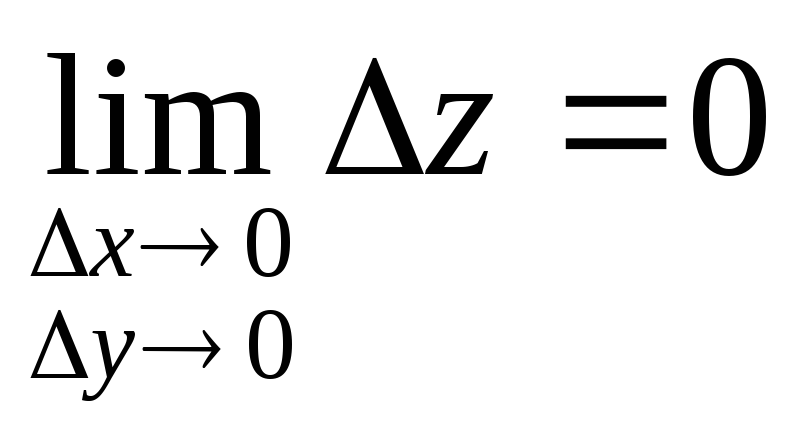Функции трех переменных

Пусть D – некоторое множество точек в трехмерном пространстве . Если каждой точкепоставлено в соответствие по некоторому правилу число, то на множествеD задана функция . Поскольку каждая точка Р определяется тремя координатами, тоесть функция трех независимых переменных, заданная на множествеD:

,

где D – область определения функции .

Пример. - объем параллелепипеда со сторонами.

пусть задана функция , тогда множество точек, в которых она принимает одно и то же значение С, называется поверхностью уровня. Ее уравнение :

.

4.2 Дифференциальное исчисление функций нескольких переменных

Дифференциальное исчисление функций двух переменных

Определение. Частными производными в точке поиназывают соответственнои.

Обозначения: ,или,, или,или,.

Пример.

, .

Определение. Выражение вида

называется полным дифференциалом функции в точке .

Производная по направлению определяет скорость изменения функции в этом направлении и вычисляется следующим образом:

,

где - угол между вектороми осью ОХ.

Градиент функции

В каждой точке областиD, где задана функция (скалярное поле), определим вектор, координатами которого будут частные производные, вычисленные в этой точке:

.

Вектор называется градиентом функции, и обозначают.

Экстремумы функции нескольких переменных

Функция в точкеимеет максимум, если в любой точкедостаточно малой- окрестности точки Р выполняется неравенство:

,

и минимум, если .

Теорема (необходимый признак экстремума функции ).

Если в точке экстремума функцияимеет частные производные первого порядка, то они равны нулю:

.

Теорема (достаточный признак экстремума функции ).

Пусть в некоторой внутренней точке областиD функция имеет непрерывные частные производные до третьего порядка включительно. Если выполнены равенстваи выражение:

,

то в точке - экстремум. При этом если, то в точке- максимум, если, то в точке- минимум.

Пример. Найти экстремумы функции .

Решение. 1) Составим и решим систему уравнений

; ;;;.

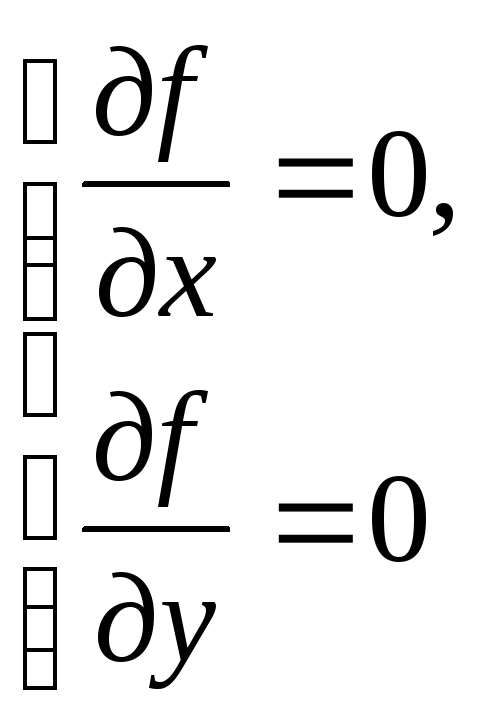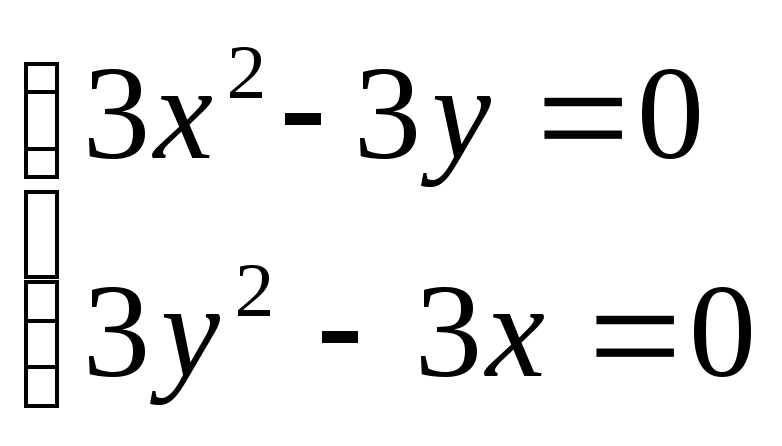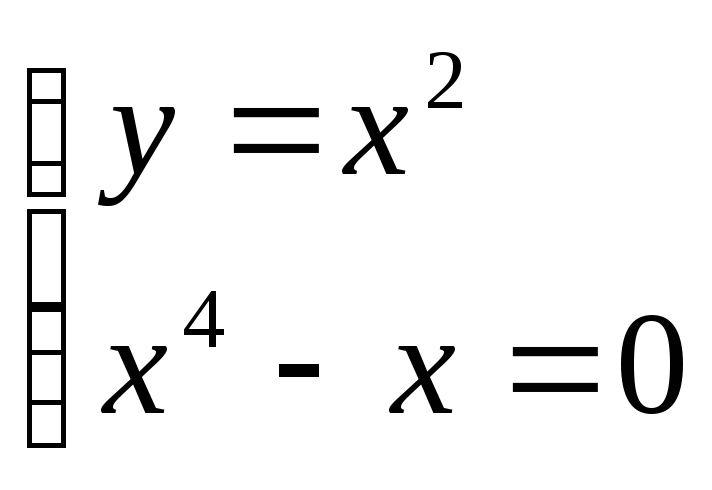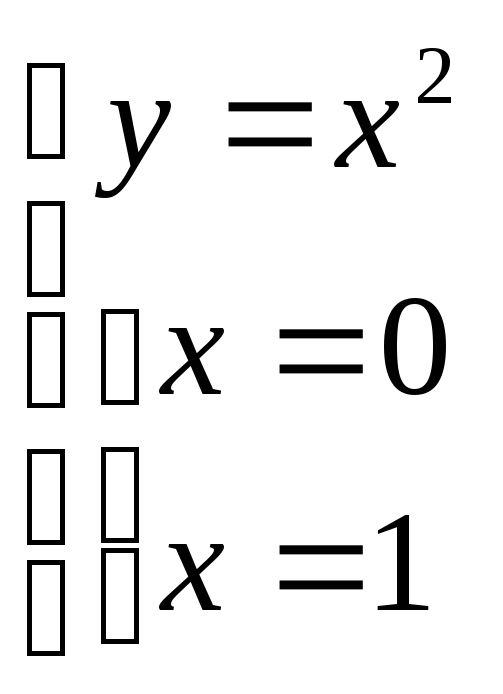Таким образом, получили две точки, «подозрительные» на экстремум:

и .

2) Вычислим вторые производные данной функции:

, ,.

Найдем значения этих производных в точках и:

а) :,,. Тогда.

Таким образом, точка не является экстремумом функции.

б) :,,. Тогда.

Таким образом, точка является экстремумом функции, а именно минимумом функции, так как.