Практическая работа №5

«Элементы теории вероятностей. Случайная величина и ее распределение»

Цель занятия: Научиться решать примеры и задачи по данной теме

Вопросы теории ( исходный уровень)

1. Элементы теории вероятностей.

2. Виды случайных событий, теоремы сложения и умножения.

3. Формула Байеса.

4. Вероятностный характер меди­ко-биологических процессов.

Основы применения вероятностных методов в диагностике и прогнозировании заболеваний (лекция №1).

Содержание занятия:

1.Ответить на вопросы по теме занятия.

2.Решить задачи и примеры.

Задачи и примеры

1.Из 982 больных, поступивших в хирургическую больницу за месяц, 275 человек имели травмы. Какова относительная частота поступления больных с этим видом заболевания?

2. В институт было подано 1275 заявлений о приеме от девушек и 1084 заявлений от юношей. Каковы относительные частоты подачи заявления для этих групп абитуриентов?

3. Грани правильного тетраэдра (рис. 1) про­нумерованы: 1, 2, 3 и 4. Какова вероятность того, что при бросании тетраэдр встанет на грань с цифрой 1? с цифрой 2? Предполагается, что тетраэдр сделан из однородного материала. Почему необходимо последнее условие?

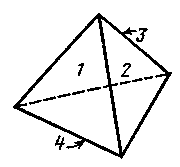
Рис. 1

4. Условие предыдущей задачи. Найти вероятность того, что на видимых (боковых) гранях тетраэдра будут цифры 1, 2 и 3?

5. В картотеке имеются истории болезней восьми пациентов. Если наугад взять первую, затем вторую, третью и т. д. историю болезней, то какова в каждом случае будет вероятность изъятия нужной истории болезней? Предполагается, что искомая история болезней имеется в картотеке. Рассмотреть два варианта: а) взятые истории болезней не возвращаются в картотеку; б) взятые истории болезней каждый раз возвращаются в картотеку и хаотически рас­полагаются в ней.

6. По гладкому столу катится однородный шар. Вследствие сил трения шар останавливается. Какова вероятность того, что шар остановится, касаясь поверхности стола заранее заданной точкой?

7. Найти вероятность выпадания нечетного числа при бросании игральной кости (однородный куб).

8. В урне находится 10 шаров: 3 белых и 7 черных. Из нее наугад извлекается один шар. Какова вероятность того, что этот шар будет белый? черный?

9. В условиях предыдущей задачи извлекается черный шар и не возвращается в урну. Какова вероятность извлечь после этого чер­ный шар? белый?

10. В условиях задачи 7.8 извлекается белый шар и не возвра­щается в урну. Какова вероятность извлечь после этого черный шар? белый?

11. В урне находится 10 шаров: 2 белых, 4 черных, 1 красный и 3 синих. Найти вероятность появления белого, или черного, или красного шара при однократной операции изъятия шара из Урны.

Укажите разные способы решения. Используйте понятие «противоположные события».

12. В некоторую больницу поступают пациенты с 4 видами бо­лезней. Многолетние наблюдения показывают, что этим группам заболеваний соответствуют вероятности: 0,1; 0,4; 0,3 и 0,2. Для лечения заболеваний с вероятностью 0,1 и 0,2 необходимо перели­вание крови. Какое количество больных следует обеспечить кровью, если в течение месяца поступило 1000 больных?

13. На странице книги имеется 2500 букв. Буква «а» встречается 225 раз. Какова вероятность того, что случайно выбранная буква будет буквой «а»? Какова вероятность, что случайно выбранная буква не есть «а»?

14. В урне имеется 7 черных и несколько белых шаров. Каков; вероятность вытащить белый шар, если вероятность вынимания черного шара равна 1/6? Сколько белых шаров в урне?

15. Какова вероятность того, что при случайном сочетании цифр 1, 2 и 3 получится число 123? не получится числа 123?

16. В урне имеется 1 черный и 4 белых шара. Шары по одному вынимаются из урны и обратно не возвращаются. Указать, чему равны вероятности вынуть черный шар при первом, втором и т. д. изъятии. Рассмотреть два варианта: а) черный шар оказывается последним; б) черный шар вынимается третьим.

17. В каждой из двух урн имеется по 2 черных и 3 белых шара. Какова вероятность одновременного вынимания из каждой урны по черному шару? по белому?

18. Какова вероятность того, что в результате бросания играль­ной кости 6 раз подряд выпадут единицы?

19. Какова вероятность того, что в результате бросания играль­ной кости шесть раз подряд выпадут следующие последовательности цифр: 1, 2, 3, 4, 5 и 6?

20. Какова вероятность того, что в результате бросания игральной кости б раз подряд выпадут только четные числа?

21. Найти вероятность того, что в семьях из двух детей оба ре­бенка (а) мальчики, (б) девочки, (в) один ребенок — мальчик, дру­гой — девочка. Считать, что вероятность рождения мальчика равна 0,515 и пол каждого последующего ребенка не зависит от пола предыдущих детей.

22. Какова вероятность, что в коллективе из 200 человек у двух лиц дни рождений совпадают?

23. В урне 10 шаров: 3 белых и 7 черных. Найти вероятностьтого, что последовательно один за другим будут вынуты шары:а) черный и белый; б) белый и черный.

24. В урне 8 шаров: 3 белых и 5 черных. Найти вероятность того,что последовательно один за другим будут вынуты два черныхшара? два белых шара?

25. Исходя из многолетних наблюдений, вызов врача в некоторый дом оценивается вероятностью 0,4. Найти вероятность того, что из 5 вызовов врача 2 вызова будут в данный дом.

26. Из десяти облигаций в тираже в среднем выигрывает одна. Какова вероятность того, что из двадцати облигаций выиграет только одна?

27. Условия предыдущей задачи. Какова вероятность того, что из десяти облигаций выиграет только одна? Поясните, почему в этом случае вероятность больше, чем в задаче 7.26?

28. Найти вероятность того, что из четырех облигаций выиграет: а) только одна; б) по крайней мере одна. Вероятность выигрыша i отдельной облигации равна 0,1.

29. Установлено, что лица из определенной группы людей заболевают в среднем два раза в году. Считая, что каждое заболевание имеет продолжительность 10 дней, получаем 365-2*10=345 дней, когда человек здоров. Таким образом, можно оценить вероятность заболевания одним человеком как р = 2/345 = 0,0058. Какова вероятность того, что из 10 человек сегодня заболевают трое? Заболевания в этой задаче рассматриваются как независимые события (без учета заражения).