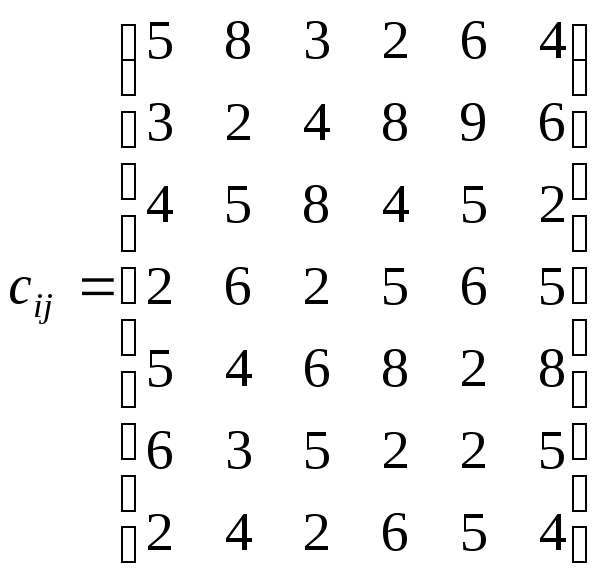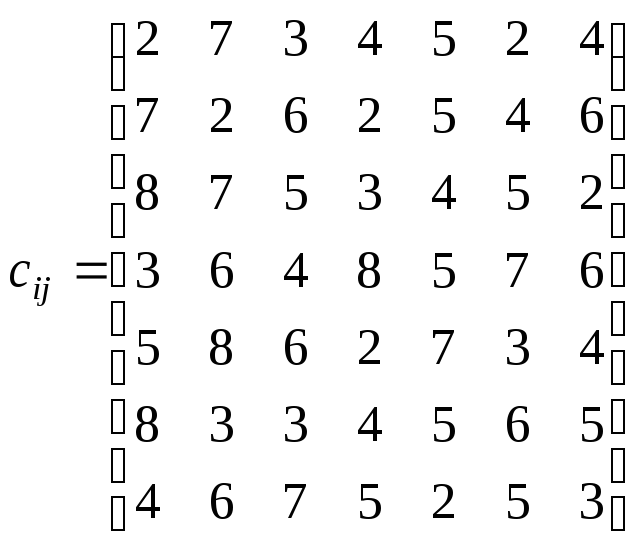Алгоритм венгерского метода решения задачи о назначениях

1. Если модель задачи открытая, то перейти к соответствующей закрытой модели задачи о назначениях.

2. Преобразовать матрицу с целью получения хотя бы одного нуля в каждой линии (строке и столбце) матрицы. Для этого

а1) если задача на максимум (т. е. - полезность), то в каждом столбце матицы выбирается максимальный элемент, из которого поочередно вычитаются элементы этого столбца и разностьзаписывается на их место;

а2) если задача на минимум (т. е. - затраты), то в каждом столбце матицы выбирается минимальный элемент, который поочередно вычитается из элементов этого столбца и разностьзаписывается на их место;

б) в каждой строке матицы выбирается минимальный элемент , который поочередно вычитается из элементов этой строки и разностьзаписывается на их место.

3. Найти в матрице максимально возможную систему независимых нулей и пометим их звездочкой (*). Для этого

а) в первом столбце выберем произвольный нуль, в последующих столбцах отмечаем нуль только в том случае, если он не находится в одной строке с уже помеченными;

б) если число независимых нулей равно n, то задача решена и оптимальные назначения определяются местами независимых нулей, а суммарная полезность (затраты) будет найдена суммированием, соответствующих оптимальным назначениям. Иначе получим максимально возможную систему независимых нулей. Для этого выделяем знаком «+» столбцы матрицы, содержащие независимые нули и рассматриваем невыделенные элементы.

• Если среди них нет нулей, то систему независимых нулей увеличить нельзя. Перейти к пункту 4.

• При наличии невыделенных нулей. Невыделенный нуль помечаем штрихом (‘) и если в этой строке есть нуль помеченный звездочкой, то выделяем строку справа знаком «+» и снимаем знак выделения столбца, содержащего нуль со звездочкой. Проделываем эти действия до тех пор пока

• все нули окажутся выделенными (в столбце или строке). Перейти к пункту 4;

• строка с нулем со штрихом не содержит нуля со звездочкой. Строим цепочку элементов, которая начинается от последнего помеченного нуля со штрихом и по столбцу проходит к нулю со звездочкой, затем к нулю со штрихом в той же строке и т. д. Начало и конец цепочки – нули со штрихом. Затем у входящих в цепочку нулей со звездочками звездочки убираем, а у нулей со штрихами штрихи заменяем звездочками. Убираем все знаки выделения в матрице кроме звездочек. При этом число независимых нулей увеличивается на единицу. Перейти к пункту 3б.

4) Увеличить число нулей в матрице. Для этого среди элементов, находящихся в невыделенных линиях (строках и столбцах), выбирается минимальный, который отнимается от невыделенных элементов и прибавляется к элементам, выделенным дважды (и в строке и в столбце). Убираем все знаки выделения в матрице. Перейти к пункту 3.

Пример 3.1

Шесть исполнителей должны выполнить шесть работ (по одной работе каждый). Прибыль (ден. ед.) при выполненииi-ым исполнителемj-ой работыизвестна:

Составить математическую модель задачи и определить, какой исполнитель должен выполнять какую работу, чтобы суммарная прибыль была максимальной.

Решение

Составим математическую модель задачи.

Введем переменные – факт назначения-го исполнителя на-ую работу (, если назначается и, если не назначается).

Цель задачи – максимальная прибыль при назначении исполнителей на работы, следовательно, целевая функция будет иметь вид:

Систем ограничений задачи:

Решим задачу венгерским методом.

Т. к. число исполнителей совпадает с числом работ, то модель задачи закрытая (см. пункт 1 алгоритма).

Преобразуем матрицу с целью получения хотя бы одного нуля в каждой линии (строке и столбце) матрицы (см. пункт 2 алгоритма). Для этого в каждом столбце матицы выбирается максимальный элемент(таблица 3.2), из которого поочередно вычитаются элементы этого столбца и разностьзаписывается на их место (таблица 3.3):

Таблица 3.2

	2	8	4	3	5	6
	7	3	5	2	7	4
	5	2	6	5	8	6
	9	7	2	6	4	9
	3	8	6	4	2	5
	7	9	3	1	7	6
	9	9	6	6	8	9

Таблица 3.3

7	1	2	3	3	3
2	6	1	4	1	5
4	7	0	1	0	3
0	2	4	0	4	0
6	1	0	2	6	4
2	0	3	5	1	3

Затем в каждой строке матицы выбирается минимальный элемент (таблица 3.4), который поочередно вычитается из элементов этой строки и разностьзаписывается на их место (таблица 3.5):

Таблица 3.4

7	1	2	3	3	3	1
2	6	1	4	1	5	1
4	7	0	1	0	3	0
0	2	4	0	4	0	0
6	1	0	2	6	4	0
2	0	3	5	1	3	0

Таблица 3.5

6	0	1	2	2	2
1	5	0	3	0	4
4	7	0	1	0	3
0	2	4	0	4	0
6	1	0	2	6	4
2	0	3	5	1	3

Итак в матрице получен хотя бы один нуль в каждой линии (таблица 3.5).

Найдем в матрице систему независимых нулей (см. пункт 3а алгоритма) (таблица 3.6) и получим максимально возможную систему независимых нулей (см. пункт 3б алгоритма) (таблица 3.6 – таблица 3.7):

Таблица 3.6

+	+	+		+
6	0*	1	2	2	2
1	5	0*	3	0	4
4	7	0	1	0*	3
0*	2	4	0	4	0
6	1	0	2	6	4
2	0	3	5	1	3

Таблица 3.7

	+	+		+
6	0*	1	2	2	2
1	5	0*	3	0	4
4	7	0	1	0*	3
0*	2	4	0	4	0’	+
6	1	0	2	6	4
2	0	3	5	1	3

Итак, все нули оказались выделенными. Перейдем к пункту 4 алгоритма. Увеличим число нулей в матрице. Для этого среди элементов, находящихся в невыделенных линиях (в таблице 3.7

выделены жирным шрифтом), выбираем минимальный, он равен «1», который отнимем от невыделенных элементов и прибавим к элементам, выделенным дважды (в таблице 3.7 подчеркнуты). Убираем все знаки выделения в матрице (таблица 3.8):

Таблица 3.8

5	0	1	1	2	1
0	5	0	2	0	3
3	7	0	0	0	2
0	3	5	0	5	0
5	1	0	1	6	3
1	0	3	4	1	2

Переходим к пункту 3 алгоритма.

Найдем в матрице систему независимых нулей (см. пункт 3а алгоритма) (таблица 3.9) и получим максимально возможную систему независимых нулей (см. пункт 3б алгоритма) (таблица 3.9 – таблица 3.14):

Таблица 3.9

+	+	+	+
5	0*	1	1	2	1
0*	5	0	2	0	3
3	7	0*	0	0	2
0	3	5	0*	5	0
5	1	0	1	6	3
1	0	3	4	1	2

Таблица 3.10

	+	+	+
5	0*	1	1	2	1
0*	5	0	2	0’	3	+
3	7	0*	0	0	2
0	3	5	0*	5	0
5	1	0	1	6	3
1	0	3	4	1	2

Таблица 3.11

	+		+
5	0*	1	1	2	1
0*	5	0	2	0’	3	+
3	7	0*	0	0’	2	+
0	3	5	0*	5	0
5	1	0	1	6	3
1	0	3	4	1	2

Таблица 3.12

	+
5	0*	1	1	2	1
0*	5	0	2	0’	3	+
3	7	0*	0	0’	2	+
0	3	5	0*	5	0’	+
5	1	0	1	6	3
1	0	3	4	1	2

Таблица 3.13

	+
5	0*	1	1	2	1
0*	5	0	2	0’	3	+
3	7	0*	0	0’	2	+
0	3	5	0*	5	0’	+
5	1	0’	1	6	3
1	0	3	4	1	2

Строка с нулем со штрихом не содержит нуля со звездочкой (таблица 3.13). Строим цепочку элементов, которая начинается от последнего помеченного нуля со штрихом и по столбцу проходит к нулю со звездочкой, затем к нулю со штрихом в той же строке (в таблица 3.13 цепочка выделена серым цветом). Затем у входящих в цепочку нулей со звездочками звездочки убираем, а у нулей со штрихами штрихи заменяем звездочками. При этом число независимых нулей увеличилось на единицу. Убираем все знаки выделения в матрице кроме звездочек (таблица 3.14).

Таблица 3.14

5	0*	1	1	2	1
0*	5	0	2	0	3
3	7	0	0	0*	2
0	3	5	0*	5	0
5	1	0*	1	6	3
1	0	3	4	1	2

Получим максимально возможную систему независимых нулей (см. пункт 3б алгоритма) (таблица 3.15 – таблица 3.18):

Таблица 3.15

+	+	+	+	+
5	0*	1	1	2	1
0*	5	0	2	0	3
3	7	0	0	0*	2
0	3	5	0*	5	0
5	1	0*	1	6	3
1	0	3	4	1	2

Таблица 3.16

+	+	+		+
5	0*	1	1	2	1
0*	5	0	2	0	3
3	7	0	0	0*	2
0	3	5	0*	5	0’	+
5	1	0*	1	6	3
1	0	3	4	1	2

Таблица 3.17

+	+	+
5	0*	1	1	2	1
0*	5	0	2	0	3
3	7	0	0’	0*	2	+
0	3	5	0*	5	0’	+
5	1	0*	1	6	3
1	0	3	4	1	2

Таблица 3.18

	+	+
5	0*	1	1	2	1
0*	5	0	2	0’	3	+
3	7	0	0’	0*	2	+
0	3	5	0*	5	0’	+
5	1	0*	1	6	3
1	0	3	4	1	2

Итак, все нули оказались выделенными. Перейдем к пункту 4 алгоритма.

Увеличим число нулей в матрице. Для этого среди элементов, находящихся в невыделенных линиях (в таблице 3.18 выделены жирным шрифтом), выбираем минимальный, он равен «1», который отнимем от невыделенных элементов и прибавим к элементам, выделенным дважды (в таблице 3.18 подчеркнуты). Убираем все знаки выделения в матрице (таблица 3.19):

Таблица 3.19

4	0	1	0	1	0
0	6	1	2	0	3
3	8	1	0	0	2
0	4	6	0	5	0
4	1	0	0	5	2
0	0	3	3	0	1

Переходим к пункту 3 алгоритма.

Найдем в матрице систему независимых нулей (см. пункт 3а алгоритма) (таблица 3.20):

Таблица 3.20

4	0*	1	0	1	0
0*	6	1	2	0	3
3	8	1	0*	0	2
0	4	6	0	5	0*
4	1	0*	0	5	2
0	0	3	3	0*	1

Т. к. число независимых нулей равно 6, задача решена, и оптимальные назначения определяются местами независимых нулей (таблица 3.20). Таким образом, матрица назначений будет иметь вид:

(ден. ед.)

Итак, суммарная прибыль будет максимальной и составит 42 ден. ед. если первого исполнителя назначить на вторую работу, второго исполнителя – на первую работу, третьего исполнителя – на четвертую работу, четвертого исполнителя – на шестую работу, пятого исполнителя – на третью работу, шестого исполнителя – на пятую работу.

Задачи

3.1 – 3.4

Для производства шести видов винтов могут быть использованы семь станков. Производительность (винтов в мин.)i-го станкапо выпуску винтовj-го видаизвестна:

3.1	3.2
3.3	3.4

Составить математическую модель задачи и определить, какой станок должен выпускать какой вид винтов, чтобы суммарная производительность была максимальной.

3.5 – 3.8

Для выполнения некоторого задания в шесть отделений связи необходимо направить по одному транспортному средству. Для этого можно использовать семь имеющихся автомобилей. Затраты (ден. ед.)i-ого автомобиляпри выполнении задания вj-ом отделении связиизвестны:

3.5	3.6
3.7	3.8

Составить математическую модель задачи и найти план распределения автомобилей по отделениям связи, минимизирующий суммарные затраты.

3.9 – 3.12

Для производства семи видов изделий могут быть использованы шесть станков. Производительность (изделий в час)i-го станкапо выпуску изделийj-го видаизвестна:

3.9	3.10
3.11	3.12

Составить математическую модель задачи и определить, какой станок должен выпускать какой вид изделий, чтобы суммарная производительность была максимальной.

3.13 – 3.16

Для выполнения семи заказов могут быть использованы шесть машин. Затраты (руб.)i-й машиныпо выполнениюj-го заказаизвестны:

3.13	3.14
3.15	3.16

Составить математическую модель задачи и определить, какая машина должна выполнять какой заказ, чтобы суммарные затраты были минимальными.

3.17 – 3.20

Семеро рабочих должны выполнить семь заказов (по одному заказу каждый). Прибыль (усл. ден. ед.) при выполненииi-ым рабочимj-го заказаизвестна:

3.17	3.18
3.19	3.20

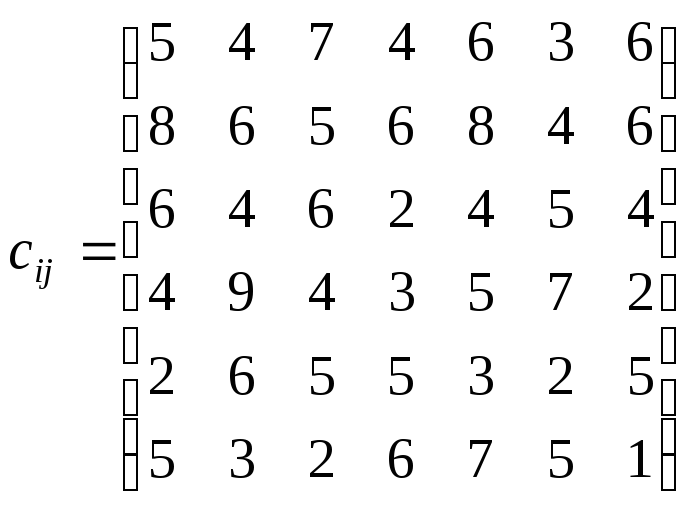
Составить математическую модель задачи и определить, какой рабочий должен выполнять какой заказ, чтобы суммарная прибыль была максимальной.

3.21 – 3.24

Семеро рабочих должны выполнить семь заказов (по одному заказу каждый). Затраты (тыс. руб.) при выполненииi-ым рабочимj-го заказаизвестны:

3.21	3.22
3.23	3.24

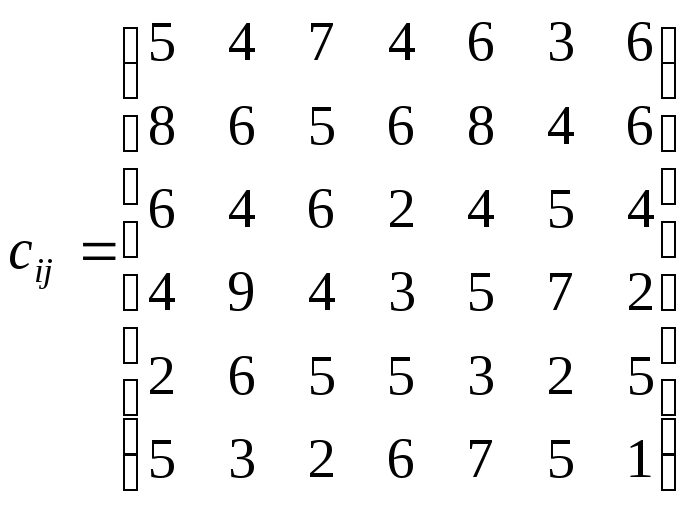
Составить математическую модель задачи и определить, какой рабочий должен выполнять какой заказ, чтобы суммарные затраты были минимальными.