Задача 3

Считая данные задачи 1 результатом собственно случайной повторной выборки из генеральной совокупности, определить:

1) точечную оценку доли участков с показателем водопотребления от 168 до 175 м³/га,

2) доверительный интервал при доверительной вероятности 0,95 ,

3) вероятность того, что ошибка выборочной доли не превысит 0,01 ,

4) необходимый объём выборки, который с вероятностью 0,95 обеспечил бы ошибку выборочной доли не более 0,01 .

Р е ш е н и е

Выборочная доля собственно случайной повторной выборки распределена по нормальному закону. Поскольку вероятность того, что отклонение случайной величины, распределённой по нормальному закону, от её математического ожидания , не превзойдёт по абсолютной величине, равна:

,

где среднее квадратическое отклонение случайной величины Х , функция функция Лапласа.

Принимая во внимание, что для выборочной доли Z математическое ожидание , дисперсия, т.е.,, то

.

1) Находим выборочную долю . Это и есть точечная оценка генеральной доли.

2) По заданной доверительной вероятности находим значение аргумента функции Лапласа

.

Применяем формулу предельной ошибки выборочной доли

.

Таким образом, доверительный интервал для генеральной доли Z равен:

или ,

т.е., с вероятностью 0,95 в генеральной совокупности будет от 8 до 28% участков с показателем водопотребления от 168 до 175 м³/га.

3) Имеем .

Отсюда .

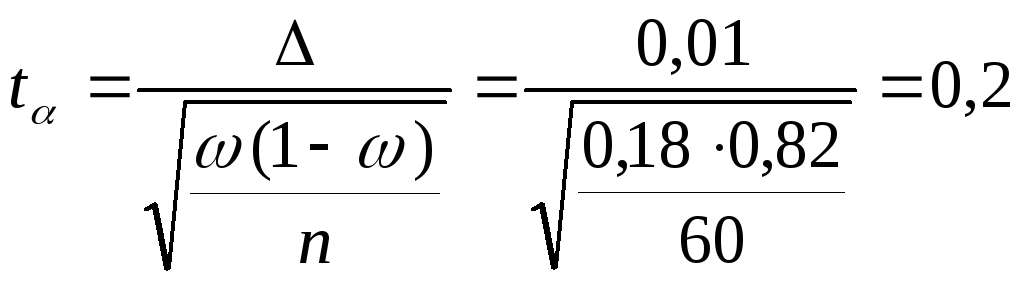По таблице интегральной функции Лапласа находим соответствующую доверительную вероятность .

4) Преобразовав соответствующим образом формулу предельной ошибки выборки, получаем

,

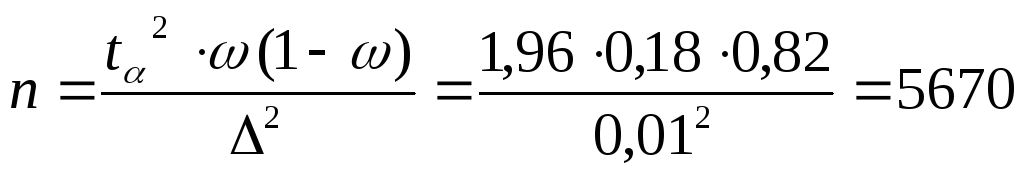т.е., сделав случайную выборку в количестве 5670 участков и определив в ней долю участков с показателем водопотребления от 168 до 175 м³/га, можно с практической достоверностью (вероятность 95%) утверждать, что процент данных участков в общем объёме будет близок к проценту данных участков в выборке (отклонение в ту или иную сторону может составить не более 1%).

Задача 4

По эмпирическому распределению, построенному в задаче 1, построить нормальное распределение; изобразить его графически на том же рисунке, на котором построено эмпирическое распределение, а также проверить статистическую гипотезу о нормальности выборочного распределения, используя критерий Пирсона при уровне значимости 0,05 .

Р е ш е н и е

Воспользуемся решением задачи 1 для определения средней и среднего квадратического отклонения в интервальном вариационном ряду:

.

Нулевую гипотезу сформулируем как утверждение, что случайная величина - показатель водопотребления в генеральной совокупности – имеет нормальное распределение с указанными выше параметрами.

Рассчитаем вероятность попадания случайной величиныв-ый интервал, а затем определим теоретические частоты.

При этом

для интервального распределения и

для дискретного распределения, где величина шага дискретного распределения.

Для упрощённого вычисления теоретических частот используется таблица

Варианты -
140-147	4	-1,5401	-2,1567	-0,4382	-0,4886	0,0504	3
147-154	8	-0,9243	-1,5401	-0,3212	-0,4382	0,117	7
154-161	10	-0,3081	-0,9243	-0,1217	-0,3212	0,1995	12
161-168	16	0,3081	-0,3081	0,1217	-0,1217	0,2434	15
168-175	11	0,9243	0,3081	0,3212	0,1217	0,1995	12
175-182	6	1,5401	0,9243	0,4382	0,3212	0,117	7
182-189	5	2,1567	1,5401	0,4886	0,4382	0,0504	3
Итого	60	-	-	-	-	-	59

Построим на одном графике теоретические и эмпирические частоты распределения:

Воспользуемся критерием Пирсона в качестве меры расхождения теоретического и эмпирического ряда частот возьмём величину

Случайная величина имеет специальное распределение, задаваемое таблично, и, зависящее от числа , называемого числом степеней свободы, где число групп эмпирического распределения,число параметров теоретического закона (, , ) , т.е.. По таблице при уровне значимостинаходим.

Если , то нулевая гипотеза Н₀ (случайная величина имеет нормальное распределение) принимается, если - отвергается.

В нашем случае , т.е. случайная величина - показатель водопотребления,распределён по нормальному закону.