ЛЕКЦИЯ 9_Динамическое_программирование

ЛЕКЦИЯ №9

Модели динамического программирования

Динамическое программирование (ДП) применяется при решении оптимизационных задач, в которых процесс принятия решений может быть разбит на этапы (шаги).

Если модели линейного программирования (ЛП) применяются в экономике для принятия крупномасштабных плановых решений в сложных ситуациях, то модели ДП применяются при решении задач значительно меньшего масштаба, например, при разработке правил управления запасами, устанавливающими момент пополнения запасов, при распределении дефицитных капитальных вложений между возможными новыми направлениями их использования, при разработке долгосрочных правил замены выбывающих из эксплуатации основных фондов и т.д.

Общая постановка задачи ДП

Рассматривается управляемый процесс, например, экономический процесс распределения средств между предприятиями, распределения ресурсов в течение ряда лет и т.п. В результате управления система (объект управления) переводится из начального состояния в состояние . Предположим, что управление можно разбить на шагов, т.е. решение принимается последовательно на каждом шаге, а управление, переводящее систему из в , можно представить в виде последовательности пошаговых управлений.

Обозначим через управление на -м шаге . Переменные удовлетворяют некоторым ограничениям и в этом смысле называются допустимыми.

Пусть - управление, переводящее систему из состояния в состояние .

Обозначим через - состояние системы после -го шага управления.

Получаем последовательность состояний системы

.

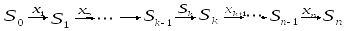
Показатель эффективности F управляемой операции (целевая функция) зависит от начального состояния и управления:

(1)

Предположим, что:

1. Состояние системы в конце -го шага зависит только от предшествующего состояния и управления на 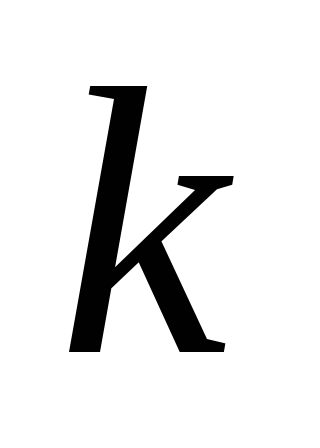-м шаге и не зависит от других предшествующих состояний и управлений. Это положение записывается в виде уравнений

(2),

которые называются уравнениями состояний.

2. Целевая функция является аддитивной: (3),

где - показатель эффективности каждого шага.

Задача ДП формулируется так:

Определить такое допустимое управление , переводящее систему из состояния в состояние , при котором целевая функция (3) принимает наибольшее (наименьшее) значение.

Особенности модели ДП.

1. Задача оптимизации интерпретируется как n-шаговый процесс управления.

2. Целевая функция (ЦФ) – сумма ЦФ на каждом шаге.

3. Выбор управления на к -ом шаге зависит только от состояния системы к этому шагу и не влияет на предшествующие шаги (нет обратной связи).

4. Состояние системы после к - го шага управления зависит от предшествующего состояния и управления.

5. На каждом шаге управление зависит от конечного числа управляющих переменных, а состояние - от конечного числа параметров.

Рассмотрим схему ДП, которая не зависит от способов задания функции и ограничений.

Принцип оптимальности и уравнения Беллмана.

Каково бы ни было состояние системы в результате какого-либо числа шагов, на ближайшем шаге управление следует выбирать так, чтобы оно в совокупности с управлениями на всех последующих шагах приводило к оптимальному выигрышу на всех последующих шагах, включая данный шаг.

Беллман также сформулировал условия, при которых принцип верен. Основное – система должна быть без обратной связи, т.е. управление на данном шаге не должно оказывать влияние на предшествующие шаги.

Принцип оптимальности утверждает, что для любого процесса без обратной связи оптимальное управление таково, что является оптимальным для любого подпроцесса по отношению к его исходному состоянию. Поэтому решение на каждом шаге оказывается наилучшим с точки зрения управления в целом.

Рассмотрим вместо исходной задачи ДП с фиксированным числом шагов и начальным состоянием последовательность задач, полагая при различных одношаговую, двухшаговую и т.д., используя принцип оптимальности.

На каждом шаге любого состояния решение влияет на последующее состояние.

Но есть один шаг, последний, который можно для любого состояния планировать условно-локально, исходя только из соображений этого шага.

Рассмотрим шаг:

- состояние системы к началу этого шага;

- конечное состояние;

- управление на шаге.

- целевая функция (выигрыш) шага.

Согласно принципу оптимальности, управление необходимо выбирать так, чтобы получить максимум на этом шаге.

Обозначим через целевой функции шага при условии, что к началу последнего шага система была в произвольном состоянии.

(4)

Максимум находится по всем допустимым управлениям . Решение , при котором достигается также зависит от и называется условно оптимальным управлением на шаге. Обозначим его через . Решив одномерную задачу локальной оптимизации по уравнению (4), получим и .

Рассмотрим теперь двумерную задачу.

Для любых состояний , произвольных управлений и оптимальных управлений значение целевой функции на двух последних шагах равно:

(5)

Согласно принципу оптимальности, необходимо выбрать решение так, чтобы значение (5) было максимальным, т.е.:

(6)

Т.к. можно найти из уравнения состояния и подставить вместо в функцию , то в результате оптимизации только по одной переменной , получим две функции:

и .

Далее рассматривается трехшаговая задача и т.д.

Обозначим через условный максимум целевой функции, полученной на шагах, начиная с до конца, при условии, что к шагу система находилась в состоянии . Фактически эта функция равна:

(7)

- условно оптимальное управление на том шаге. Чтобы его найти, необходимо вместо подставить .

Уравнение (7) называется основным рекуррентным соотношением Беллмана (ОРС).

Управление - называется условно-оптимальным управлением на шаге.

Таким образом, зная уравнение состояний и пользуясь ОРС (7), можно получить две последовательности:

Условный максимум целевой функции за n шагов:

.

Далее, используя последовательность условных оптимальных управлений и уравнение состояния, находим оптимальное решение задачи ДП.

Схема метода

1. Рассматриваем последний шаг и находим условный максимум целевой функции на этом шагепо всем возможным управлениям .

2. Для каждого значения находим условный максимум целевой функции за шагов, начиная с до конца по всем возможным управлениям :

где: Получаем последовательности и

условных оптимумов и условно оптимальных решений соответственно.

3. Значение и есть оптимум. Пользуясь уравнением состояния, находим оптимальное решение .

6