
- •Міністерство освіти і науки, молоді та спорту україни
- •Означений інтеграл
- •Означений інтеграл. Теорема про існування означеного інтеграла
- •1.2. Основні властивості означеного інтеграла
- •2. Обчислення означеного інтеграла. Формула ньютона-лейбніца
- •3.Заміна змінної у означеному інтегралі
- •Інтегрування частинамиу означеному інтегралі
- •5. Невластиві інтеграли
- •5.1. Невластиві інтеграли з нескінченними границями
- •5.2. Інтеграли від розривних функцій
- •6. Геометричні та механічні застосування означеного інтеграла
- •6. 1. Обчислення площ у прямокутних координатах
- •6. 2. Обчислення площі криволінійної трапеції, якщо крива задана рівняннями у параметричному вигляді
- •6. 3. Площа криволінійного сектора у полярних координатах
- •6. 4. Довжина дуги кривої
- •6. 5. Довжина дуги у полярних координатах
- •6.6. Обчислення об’ємів тіл за поперечними перетинами
- •6. 7. Об'єм тіла обертання
- •6. 8. Площа поверхні тіла обертання
- •6. 9. Обчислення роботи за допомогою визначеного інтеграла
- •7. Завдання для самостійної роботи
- •Література
7. Завдання для самостійної роботи
1. Обчислити інтеграли:
1)
 .
2)
.
2) .
.
3)
 .
4)
.
4) .
.
5)
 .
6)
.
6) .
.
7) .
8)
.
8) .
.
9)
 .
10)
.
10) .
.
11)
 .
12)
.
12)
13)
 14)
14)
15)
 16)
16)


35
19)
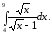 20)
20) .
.
21)
 22)
22)
23)
 24)
24)
25)
 26)
26)
27*)
 28*)
28*)



2. Обчислити невластиві інтеграли або встановити їх розбіжність (№№ 1 – 24); дослідити збіжність інтегралів
(№№ 25 – 30):
1)
 2)
2)

3)
 .
4)
.
4)

5)
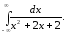 6)
6)

7)
 8)
8)

36


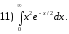

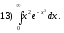

 16)
16)

17)












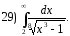

3. Застосування означеного інтеграла
Обчислити площі фігур, обмежених наступними лініями (1-25):
37
1)
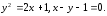 2)
2)


3)
 4)
4)
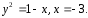
5)
 6)
6)

7)
 8)
8)
9)

10)

11)
 12)
12)

13)
 14)
14)

15)
 16)
16)

17)
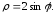 18)
18)

19)
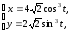
 20)
20)

21)

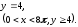 22)
22)


23)

 24)
24)


25)


38
26).
Круг
 поділенний параболою
поділенний параболою на
дві частини. Знайти площі обох частин.
на
дві частини. Знайти площі обох частин.
27).
Знайти площу фігури, обмеженої однією
аркою циклоїди

 та віссю абсцис.
та віссю абсцис.
Знайти довжини дуг наступних ліній (28 - 42):
28)
 від
від
 до
до 29)
29)
 від
від до
до
30)

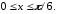
31)
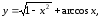

32)
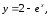

33)


34)


35)


36)


37)
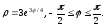 38)
38)
39)
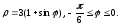 40)
40)

41)
 42)
42)

39
43).
Знайти довжину дуги спіралі Архімеда
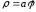 від початку до кінця першого завитка.
від початку до кінця першого завитка.
44).
Знайти довжину однієї арки циклоїди

 .
.
45).
Знайти довжину дуги лінії
 від
від
 до
до

46). Знайти площу поверхні тіла, що одержується при обертанні кола
 навколо
осі
навколо
осі

47).
Знайти площу поверхні тіла, що одержується
при обертанні синусоїди
 (від
(від до
до )
навколо осі
)
навколо осі
48).
Знайти площу поверхні тіла, що одержується
при обертанні однієї арки циклоїди

 навколо осі
навколо осі
Знайти
об'єми тіл, що одержуються при обертанні
навколо осі
 фігур,
обмежених лініями:
фігур,
обмежених лініями:
49)
 50)
50)
 (від
(від до
до ).
).
51)
 52)
52)

53)
 54)
54)

55)

Знайти об'єми тіл, що одержуються при обертанні навколо осі
 фігур,
обмежених лініями:
фігур,
обмежених лініями:
56)
 57)
57)

58)

59).
Знайти об'єм тіла, яке одержується при
обертанні навколо осі
 фігури,
обмеженої параболою
фігури,
обмеженої параболою та віссю абсцис.
та віссю абсцис.
60). Обчислити об'єм тіла, обмеженого еліптичним параболоїдом
 та
площиною
та
площиною

61).
Обчислити об’єми тіл, обмежених
параболоїдом
 та
еліпсоїдом
та
еліпсоїдом
62).
Обчислити об'єм еліпсоїда

63).
Знайти об'єм тіла, обмеженого поверхнями
 40
40
Знайти об'єми тіл, обмежених поверхнями (64 – 66):
64)
 65)
65)

66)

67).
Швидкість тіла дається формулою
 м/сек.
Знайти відстань, що пройде тіло за перші
10 сек.
після початку руху.
м/сек.
Знайти відстань, що пройде тіло за перші
10 сек.
після початку руху.
68).
При гармонійному коливальному русі
вдовж осі абсцис навколо початку
координат швидкість описується формулою
 (
( - час,
- час, -
період коливань,
-
період коливань, -
початкова фаза). Знайти положення точки
у момент часу
-
початкова фаза). Знайти положення точки
у момент часу ,
якщо відомо, що у момент
,
якщо відомо, що у момент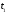 вона
знаходилась у точці
вона
знаходилась у точці

69).
Визначити роботу, яку треба витратити,
щоб підняти масу
 з
поверхні землі на висоту
з
поверхні землі на висоту
 .
.
Вказівка.
Сила
 земного
тяжіння на відстані
земного
тяжіння на відстані від центру землі визначається з пропорції
від центру землі визначається з пропорції ,
де
,
де -
радіус землі.
-
радіус землі.
70). Обчислити роботу розтягування на 0,001 м мідного дроту довжиною 1 м з радіусом перетину 2 мм.
Вказівка.
Сила
 Н
натягнення дроту довжиною 1м
та площею перетину
Н
натягнення дроту довжиною 1м
та площею перетину
 при
подовженні її на
при
подовженні її на м
визначається
формулою
м
визначається
формулою
 ,
де
,
де -
модуль пружності. (Для міді треба прийняти
-
модуль пружності. (Для міді треба прийняти Н/мм2).
Н/мм2).
41
