
- •Міністерство освіти і науки, молоді та спорту україни
- •Означений інтеграл
- •Означений інтеграл. Теорема про існування означеного інтеграла
- •1.2. Основні властивості означеного інтеграла
- •2. Обчислення означеного інтеграла. Формула ньютона-лейбніца
- •3.Заміна змінної у означеному інтегралі
- •Інтегрування частинамиу означеному інтегралі
- •5. Невластиві інтеграли
- •5.1. Невластиві інтеграли з нескінченними границями
- •5.2. Інтеграли від розривних функцій
- •6. Геометричні та механічні застосування означеного інтеграла
- •6. 1. Обчислення площ у прямокутних координатах
- •6. 2. Обчислення площі криволінійної трапеції, якщо крива задана рівняннями у параметричному вигляді
- •6. 3. Площа криволінійного сектора у полярних координатах
- •6. 4. Довжина дуги кривої
- •6. 5. Довжина дуги у полярних координатах
- •6.6. Обчислення об’ємів тіл за поперечними перетинами
- •6. 7. Об'єм тіла обертання
- •6. 8. Площа поверхні тіла обертання
- •6. 9. Обчислення роботи за допомогою визначеного інтеграла
- •7. Завдання для самостійної роботи
- •Література
5.2. Інтеграли від розривних функцій
Нехай
функція
 визначена і неперервна при
визначена і неперервна при ,
а при
,
а при вона або не визначена, або має розрив.
У цьому випадку не можна казати про
інтеграл
вона або не визначена, або має розрив.
У цьому випадку не можна казати про
інтеграл як границю інтегральних сум, оскільки
як границю інтегральних сум, оскільки не є неперервною на відрізку
не є неперервною на відрізку ,
і ця границя може не існувати. Інтеграл
,
і ця границя може не існувати. Інтеграл від функції
від функції ,
що має розрив у точці
,
що має розрив у точці ,
визначається наступним чином:
,
визначається наступним чином: =
= .
.
Якщо остання границя існує, то інтеграл називається збіжним інтегралом, у протилежному випадку – розбіжним.
Якщо
функція
 розривна на лівому кінці відрізка
розривна на лівому кінці відрізка (тобто при
(тобто при ),
то за визначенням
),
то за визначенням
 =
= .
.
Якщо
функція має розрив у деякій точці
 ,
де
,
де ,
то покладають:
,
то покладають:
 .
Якщо обидва інтеграла
.
Якщо обидва інтеграла
у
правій частині останньої рівності
існують, то існує
(збігається) інтеграл
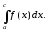 18
18
Приклад
17
.
Обчислити
 .
.
За
визначенням

 .
.
Приклад
18
.
Обчислити
 або встановити його розбіжність.
Очевидно, що при
або встановити його розбіжність.
Очевидно, що при підінтегральна функція має нескінченний
розрив. Тому даний інтеграл треба
представити у вигляді суми двох
інтегралів:
підінтегральна функція має нескінченний
розрив. Тому даний інтеграл треба
представити у вигляді суми двох
інтегралів:

 .
Кожний з інтегралів
.
Кожний з інтегралів
 та
та треба
шукати окремо:
треба
шукати окремо: .
Аналогічно встановлюється розбіжність
інтеграла
.
Аналогічно встановлюється розбіжність
інтеграла .
Але в цьому немає необхідності, тому що
для збіжності інтеграла треба, щоб
збігались обидва інтеграли
.
Але в цьому немає необхідності, тому що
для збіжності інтеграла треба, щоб
збігались обидва інтеграли та
та .
Тому незалежно від поведінки
.
Тому незалежно від поведінки даний інтеграл розбігається. Зауважимо,
що якщо би ми обчислювали інтеграл, не
звернувши уваги на розрив підінтегральної
функції при
даний інтеграл розбігається. Зауважимо,
що якщо би ми обчислювали інтеграл, не
звернувши уваги на розрив підінтегральної
функції при ,
то одержали б помилковий результат.
Дійсно,
,
то одержали б помилковий результат.
Дійсно, =
= ,
що неможливо (див. рис.5.4).
Таким
чином, неодмінно звертайте увагу на
поведінку підінтегральної функції на
відрізку інтегрування!
,
що неможливо (див. рис.5.4).
Таким
чином, неодмінно звертайте увагу на
поведінку підінтегральної функції на
відрізку інтегрування!
Рис.
5.4
19
Зауваження.
Якщо функція
 ,
визначена на відрізку
,
визначена на відрізку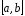 , має в середині цього відрізка кінцеву
кількість точок розриву
, має в середині цього відрізка кінцеву
кількість точок розриву ,
то інтеграл від функції
,
то інтеграл від функції на
відрізку
на
відрізку визначається у вигляді суми
визначається у вигляді суми
 ,
,
якщо
кожний з невластивих інтегралів у правій
частині збігається. Якщо принаймні один
з них розбігається, то
 називається розбіжним.
називається розбіжним.
Для встановлення збіжності невластивих інтегралів від розривних функцій та оцінки їх значення можуть бути використані теореми, аналогічні теоремам для оцінки інтегралів з нескінченними границями.
Теорема
1*.
Якщо на відрізку
 функції
функції та
та розривні
у точціс,
причому, у всіх точках цього відрізка
виконані нерівності
розривні
у точціс,
причому, у всіх точках цього відрізка
виконані нерівності
 і збігається інтеграл
і збігається інтеграл ,
тоді інтеграл
,
тоді інтеграл також збігається.
також збігається.
Теорема
2*. Якщо
на відрізку
 функції
функції та
та розривні
у точціс,
причому у всіх точках цього відрізка
виконані нерівності
розривні
у точціс,
причому у всіх точках цього відрізка
виконані нерівності
 і розбігається інтеграл
і розбігається інтеграл ,
тоді інтеграл
,
тоді інтеграл також розбігається.
також розбігається.
Теорема
3*. Якщо
на відрізку
 знакозмінна функція
знакозмінна функція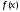 має розрив лише у точціс
і невласний інтеграл
має розрив лише у точціс
і невласний інтеграл
 від абсолютної величини цієї функції
збігається, то інтеграл
від абсолютної величини цієї функції
збігається, то інтеграл
 також збігається.
також збігається.
У
якості функції, із якою порівнюють
підінтегральну функцію, часто обирають
 .
Легко перевірити, що
.
Легко перевірити, що збігається при
збігається при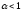 ,
розбігається при
,
розбігається при .
.
20
Те
ж саме справедливо для інтегралів
вигляду
 .
.
Приклад
19
.
Чи збігається
 ?
?
Підінтегральна
функція має розрив при х
= 0.
Порівнюючи її із функцією
 ,маємо
,маємо Невласний інтеграл
Невласний інтеграл існує. Отже, невластивій інтеграл від
«меншої» функції, тобто
існує. Отже, невластивій інтеграл від
«меншої» функції, тобто
 також існує.
також існує.
