МIНIСТЕРСТВО ОСВIТИ І НАУКИ УКРАЇНИ Національний унiверситет "Львiвська полiтехнiка"

СТАТИСТИЧНІ МЕТОДИ В ПРОЕКТУВАННІ СОС. Попередня обробка експериментальнних даних.

Дисперсійний аналіз.

МЕТОДИЧНІ ВКАЗІВКИ

до лабораторної роботи № 1 з курсу "Основи автоматизованого проектування

складних об’єктів і систем"

для студентiв базового напрямку 6.0804 "Комп'ютернi науки"

Затвердженона засiданнi кафедри ″Системи автоматизованого проектування"

Протокол N 1 вiд 27.08.2001р.

Львiв 2001

1МЕТА РОБОТИ

•вивчити основні методи статистичного аналізу

•здійснити попередню обробку експериментальних данних

•провести дисперсійний аналіз отриманої виборки.

2КОРОТКІ ТЕОРЕТИЧНI ВIДОМОСТI

2.1Застосування статистичних методів аналізу

Як правило більшість систем в фізиці, хімії, технології, економіці та ін. областях являються дуже складними і, при неповному знанні всього механізму СОС, їх можна досліджувати лише експериментально. Тому, для їх вивчення проводять серії експериментів, які пов`язані з вимірюванням різних фізичних величин. В силу природи вимірів і в силу флуктуації умов експерименту, завжди буде спостерігатись розкид чи розсіювання вихідних параметрів. Тому, такі експериментальні дані представляють собою вибірку з деякого розподілу. Вибіркою називають частину експериментів, відібраних для досліджень з загальної сукупності експериментів, яку називають генеральною сукупністю. Якщо вибірка достатньо точно представляє відповідні характеристики генеральної сукупності, то таку вибірку називають

репрезентативною.

З точки зору математики і статистики, безпосереднім завданням експерименту є організація репрезентованої вибірки. В результаті обробки даних отримується емпірична математична модель об`єкта, яка справедлива у тій області значень факторів (вхідних параметрів), в якій вони змінюються у процесі експерименту. Отримана модель може бути використана для оптимізації та автоматичного управління досліджуваного процеса.

3

Математично задача формулюється наступним чином: необхідно отримати модель функціональної залежності

де y -параметр процеса, котрий необхідно оптимізувати; (х1 , х2 , ... , хn) - незалежні змінні, які можна змінювати в процесі експериментів.

Змінні (х1 , х2 , ... , хn) називають факторами, а координатний простір з координатами х1 , х2 , ... , хn – факторним простором. Геометричний образ, який відповідає функції відгука, називають поверхнею відгука.

В статистиці також існує поняття генеральної сукупності. Генеральна сукупність - сукупність усіх можливих значень експериментів, які могли б бути при даному комплексі умов. Результати обмеженого ряду спостережень розглядаються як вибірка з даної генеральної сукупності.

2.2Попередня обробка результатів експериментів.

Попередня обробка результатів спостережень необхідна для того, щоб в подальшому з найбільшою ефективністю, а головне - коректно, використовувати для побудови емпіричних залежностей статистичні методи. Часто помилки у вхідних експериментальних даних приводять до значних похибок статистичного аналізу. Інколи такі результати можна інтерпритувати, інколи – ні, але такі результати завжди будуть неточними. Тому, перш ніж проводити будь-який аналіз необхідно провести первинну обробку вхідних даних.

Зміст попередньої обробки, в основному, полягає в тому, щоб відсіяти грубі похибки, які можуть зявлятись в експериментальних даних. На сьогоднішній день існує велика кількість рекомендацій для проведення відсіювання грубих похибок. Для прикладу розглянемо найпростіші.

4

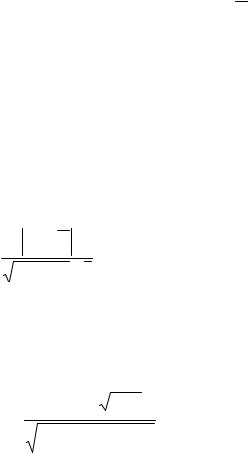
1.Метод обчислення максимального відносного відхилення:

де Xi - крайній найбільший чи найменший елемент

вибірки, по якій підраховувалися математичні сподівання X;τ - табличне значеня статистики τ, обчислене при довірчій ймовірності q=1-p.

Якщо умова (3) виконується, то спостереження не відсіюють; якщо не виконується його необхідно відсіяти. Для відсіювання того чи іншого спостереження по скороченій вибірці користуються квантованим рівнем значимості р: р=(0.100; 0.050; 0.025). На практиці в більшості випадків використовують р=0.05.

2. Метод відсіювання грубих похибок для малої вибірки:

Аналогічно, отриманий результат порівнюється з табличним значенням.

3.Для великих вибірок найкраще зарекомендували себе таблиці розподілу Ст’юдента

де t (p,n-2) - критичне значення розподілу Ст’юдента.

5

Процедура відсіювання грубих похибок результатів вимірювань з допомогою таблиць Ст’юдента проводиться за таким алгоритмом:

1.Вибираємо спостереження, що має найбільше відхилення.

2.Обчислюємо τ = Xi - X / S .

3. За таблицею знаходимо точки розподілу Ст’юдента t (0.1%,n-2) і

t (5%,n-2) .

4. За формулою (4) обчислюємо відповідні точки для

t(0.1%,n) ³ t(5%,n).

Врезультаті роботи алгоритму ми можемо отримати один з трьох результатів:

1.τ ≤ t(5%,n),

2.t(5%,n) < τ < t(0.1%,n),

3.τ > t(0.1%,n) .

Спостереження, які попали у першу групу, не відсіюються. Спостереження, які попали в другу групу, можна відсіяти, якщо на користь цього є ще якісь інші погляди дослідника. Спостереження третьої групи відсіюються завжди.

В загальному випадку, при знаходженні викиду, реакція може бути двоякою:

1.Їх можна видалити з аналізу, оскільки ці значення не відносяться до досліджуваної популяції. А потім ці викиди рекомендується досліджувати окремо, так як вони можуть давати корисну інформацію з точки зору пошуку екстремума.

2.Можна залишити ці експерименти в наборі даних для подальшого аналізу, якщо з фізичної точки зору вони є коректними. Але при цьому необхідно застосовувати процедури статистичного аналізу, які не чутливі до вхідних даних, тобто робастні процедури.

6