Лабораторна6

МІНІСТЕРСТВО ОСВІТИ І НАУКИ НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ „ЛЬВІВСЬКА ПОЛІТЕХНІКА”

АФІННІ ПЕРЕТВОРЕННЯ

МЕТОДИЧНІ ВКАЗІВКИ

до виконання лабораторної роботи №6 з дисципліни „Комп’ютерна графіка” для студентів спеціальності

6. 050103 „Програмна інженерія”

Затверджено на засіданні кафедри

програмного забезпечення Протокол № __ від _______ р.

Львів – 2013

1

Фрактали. : Методичні вказівки до виконання лабораторної роботи №6 із дисципліни „Комп’ютерна графіка” для студентів спеціальності „Програмна інженерія” / Укл.: Є.В. Левус, О.О. Нитребич – Львів: Видавництво Національного університету „Львівська політехніка”, 2013. – ?? с.

Відповідальний за випуск Федасюк Д.В., д-р тех. наук, проф.

2

Мета роботи: Ознайомитись на практиці із основними поняттями афінних перетворень, навчитись застосовувати основні перетворення – зсув, масштаб та поворот об’єктів у декартовій системі координат.

Теоретичні відомості

Виконання різноманітних дій з геометричними об’єктами є центральною задачею в комп’ютерній графіці. Тому вибір математичних методів і алгоритмів для її реалізації суттєво впливає на ефективність цілої графічної системи. У сучасній комп’ютерній графіці досить широко використовується метод координат, оскільки графічне зображення складається з пікселів, які задаються координатами. Крім цього, координати використовуються для опису розміщення об’єктів та для створення зображень шляхом перетворень з однієї системи координат в іншу.

1.Найпростіші двовимірні афінні перетворення

Афінним називається перетворення, що має такі властивостями:

● будь-яке афінне перетворення може бути представлене як послідовність операцій з числа найпростіших: зсув, розтягнення/стиснення, поворот;

● зберігаються прямі лінії, паралельність прямих, відношення довжин відрізків, що лежать на одній прямій, і відношення площ фігур.

Афінні перетворення координат на площині: (X, Y) – двовимірна система координат,

(x, y) – координати старої системи в новій системі координат.

X Ax By C

Y Dx Ey F .

Загальний вигляд афінного перетворення:

де A, B, C, D, E, F – константи. Обернене перетворення теж є афінним:

x A X B Y C ,y D X E Y F .

Найпростіші афінні перетворення об’єкта на площині.

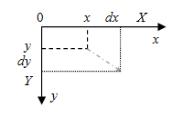
1. Здвиг об’єкта:

X x dx

Y y dy

3

Рис. 1 Зсув об’єкта

Обернене перетворення задається формулами :

x X dx

y Y dy

або відповідною матрицею:

Примітка! У літературі часто використовують іншу матрицю зсуву координат об’єкта:

З використанням даної матриці, нові координати об’єкту утворюються внаслідок множення старих координат на дану матрицю [X,Y,1]=[x,y,1] M.

2. Масштабування об’єкту:

X xkx ,

Y yky

а в матричній формі:

4

2. Тривимірні перетворення

Подібно до двовимірних афінних перетворень, під час роботи з якими з використанням однорідних координат, здійснюють дії над матрицями 3х3, тривимірні перетворення можуть бути представлені матрицею 4х4.

Отже, аналогічно двовимірному випадку матриця зсуву матиме вигляд:

а нові координати обчислюватимуться за формулою[X,Y,Z,1]= [x,y,z,1] M. Матриця масштабування –

тоді нові координати обчислюватимуться за формулою[X,Y,Z,1]=[x,y,z,1] S. Стосовно матриці повороту, то в залежності від вибраної осі матимемо такі

матриці:

- поворот відносно осі OZ:

[X,Y,Z,1]=[x,y,z,1] P.

7

3. Визначення матриці перетворень

Складним (комбінованим) називається перетворення, яке містить ланцюжок базових перетворень (не менше двох). Зауважимо, що майже всі афінні перетворення залежать від порядку їх виконання. Наприклад, перетворення повороту не комутативні ( x y y x ).

Найчастіше на практиці для визначення матриці перетворень використовують рівняння:

M K 1K* ,

що випливає із рівняння афінних перетворень K* K M , де K – матриця координат об’єкту до перетворення, K * – після перетворення, М – матриця перетворення.

Приклад 1. Знайти матрицю перетворення трикутника Р1Р2Р3 у трикутник

P1′P2′P3′ (рис. 4)

Рис. 4 Перетворення трикутників Однорідні координати вершин трикутника Р1Р2Р3 складають матрицю

8

4. Деякі правила виконання перетворень

Для представлення даних та виконання різноманітних перетворень використовуються певні узгодження. Найбільшу увагу потрібно приділяти формулюванню завдання та інтерпретації результатів. Наприклад, перед виконанням повороту необхідно отримати відповіді на наступні питання:

У правосторонній чи лівосторонній системі координат ( у залежності від взаємного розміщення напрямків координатних осей, розрізняють правосторонню та лівосторонню координатні системи, рис. 4) визначаються координатні вектори?

Обертається об'єкт або система координат?

Поворот здійснюється за чи проти годинникової стрілки?

Координати записуються у вигляді рядка або стовпця матриці?

Навколо якої лінії або осі здійснюється поворот?

а) б)

Рис.4 Типи систем координат а) правостороння; б) лівостороння.

Нехай маємо правосторонню систему координат, об'єкт обертається в нерухомій координатної системі, поворот визначається правилом правої руки (тобто поворот за годинниковою стрілкою) і координатні вектори представляються у вигляді рядка матриці.

Так як вектор задається рядком матриці, то матрицю перетворення слід розмістити після даних (матриці координатних векторів). Це перетворення задається шляхом множення справа. У разі однорідних координат для повороту об'єкта за годинникової стрілкою на кут навколо початку координат (осі OZ) використання множення праворуч приводить до наступного результату:

9

Якщо ми виразимо координатні вектори, задані в однорідних координатах у вигляді стовпця матриці, то поворот можна виконати наступним чином:

Для того, щоб повернути систему координат і залишити незмінними координатні вектори, необхідно кут замінити на .

Рис. 5 Перетворення координатних векторів та системи координат

10