
- •Основи логіки методичні вказівки
- •Основи логіки
- •Теоретичні відомості
- •1. Вступ
- •2. Логіка висловлювань
- •3. Закони логіки висловлювань
- •4. Способи доведення логічних тверджень
- •5. Логіка предикатів
- •6. Закони логіки першого ступеня
- •7. Випереджена нормальна форма
- •8. Завдання до виконання
- •9. Контрольні запитання.
- •Список літератури
- •Основи логіки методичні вказівки
6. Закони логіки першого ступеня
Основні закони логіки першого ступеня (логіки предикатів):
(xP(x))=
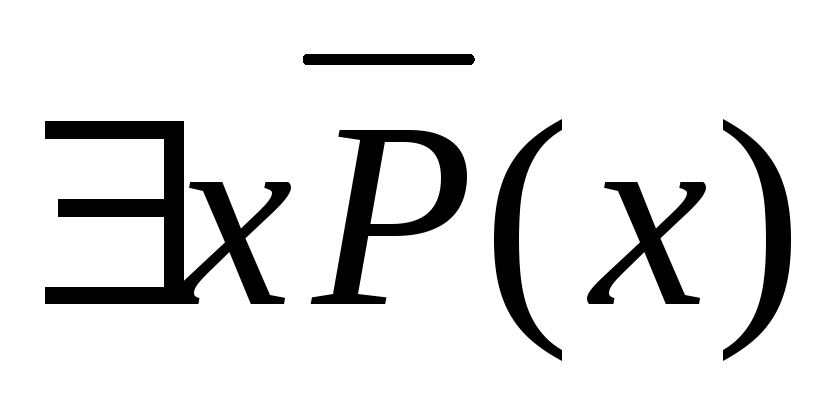 .
.(xP(x))=
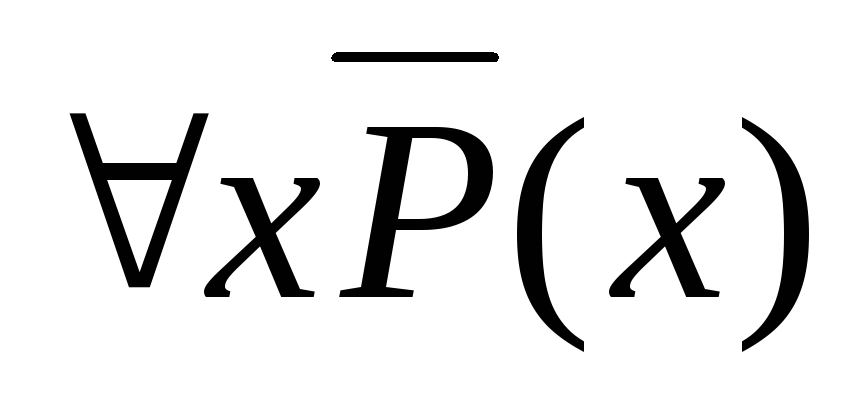 .
.x(P(x)Q(x))=xP(x)xQ(x).
x(P(x)Q(x))= xP(x) xQ(x).
x(P(x)Q)=xP(x)Q.
x(P(x)Q)=xP(x)Q.
x(P(x)Q)= xP(x)Q.
x(P(x)Q)= xP(x)Q.
xyP(x,y)= yxP(x).
xyP(x,y)= yxP(x).
Закони
1-2 дозволяють будувати заперечення
формул з кванторами. Наприклад,
xy(P(x)Q(x,y))=![]() .
.
Закони 3-4 виражають закони дистрибутивності квантора загальності відносно кон’юнкції та квантора існування відносно диз’юнкції.
Закони 5-8 дозволяють виносити за межі дії квантора, що зв’язує змінну х та формулу, яка не містить х.
Закони 9-10 свідчать про комутативність однойменних кванторів. Тобто однойменні квантори можна міняти місцями, а різнойменні – ні.
Потрібно зауважити, що у наведених формулах вказані лише зв’язані змінні і не вказані вільні змінні, що можуть набувати довільні значення із предметної області.
7. Випереджена нормальна форма
Означення 7.1. Випереджена нормальна форма – формула, записана у вигляді Q1x1Q2x2...QnxnM, де кожне Qixi (i = 1,2,...,n) –це xi або xi, а формула M не містить кванторів. Вираз Q1x1...Qnxn називають префіксом, а M – матрицею формули, записаної у випередженій нормальній формі.
Приклад 7.1. Наведемо приклади формул, записаних у випередженій нормальній формі.
1. xy(P(x,y)Q(y)).
2. xy(P(x)Q(y)).
3. xyz(Q(x,y)R(z)).
4. xyzu(P(x,z)P(y,z)Q(x,y,u)). ▲
Для того, щоб перевести формулу у випереджену нормальну форму, необхідно виконати наступні перетворення:
Використати правила усунення імплікації (PQ=
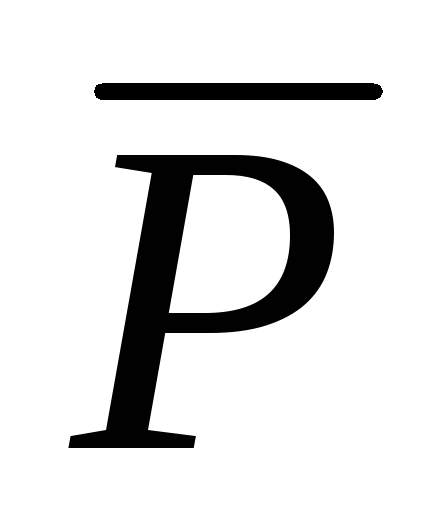 Q)
та еквівалентності (P~Q=(PQ)(QP)
).
Q)
та еквівалентності (P~Q=(PQ)(QP)
).Застосувати закон подвійного заперечення (
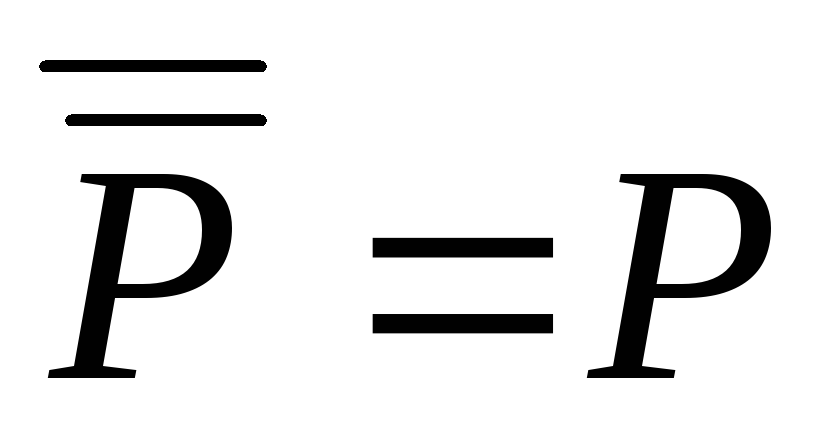 )
та закони де Моргана (
)
та закони де Моргана (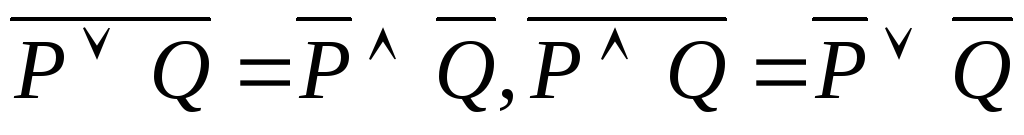 ).
).Застосувати закони: (xP(x))=
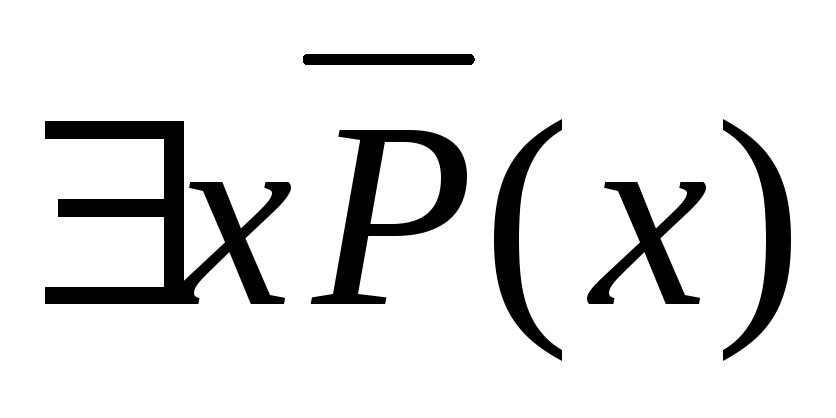 та (xP(x))=
та (xP(x))=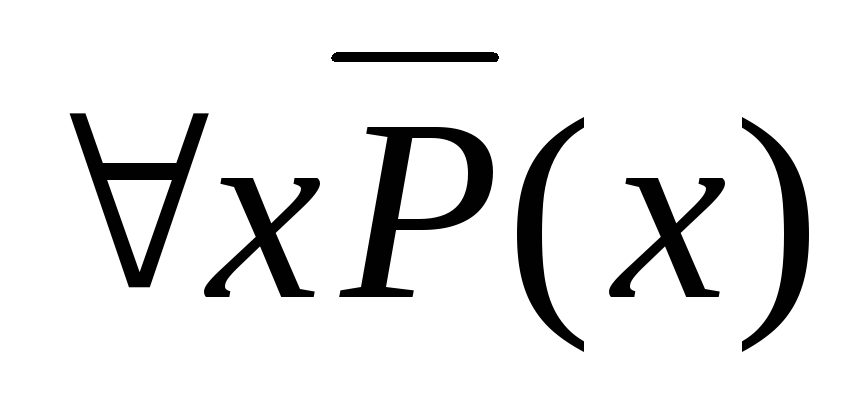 .
.
Застосувати закони логіки першого ступеня 3-8.
Винести квантори у префікс, для чого скористатись законами логіки першого ступеня 3-8.
Приклад 7.2. Зведемо формулу xP(x)→уQ(y) до випередженої нормальної форми за умови, що предикати P(x) і Q(y) не містять вільних змінних. Кроки для побудови випередженої нормальної форми:
Вилучення імплікації:
xP(x)→уQ(y)= (xP(x))уQ(y).
Застосування закону (xP(x))=
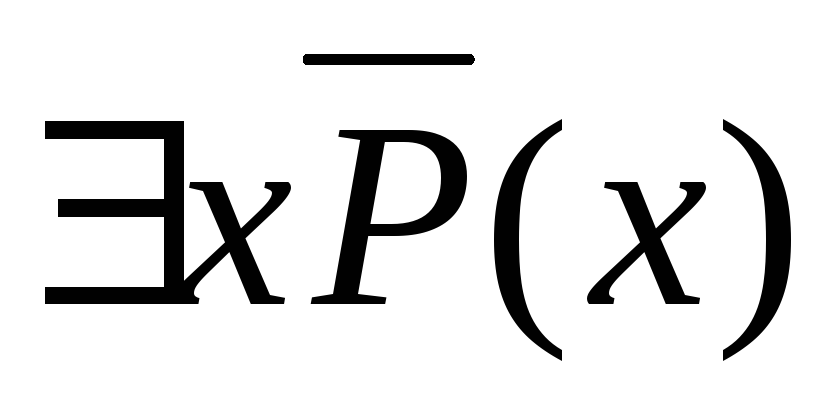 :
:
(xP(x))уQ(y)=
![]() ))уQ(y).
))уQ(y).
Винесення квантора існування у префікс:
![]() ))уQ(y)
=ху(
))уQ(y)
=ху(![]() Q(y)).
▲
Q(y)).
▲
Приклад 7.3. Зведемо формулу xy(zP(x,z) P(y,z)) uQ(x,y,u)) до випередженої нормальної форми. Кроки для побудови випередженої нормальної форми:
Вилучення імплікації:
xy(zP(x,z) P(y,z)) uQ(x,y,u))= xy((zP(x,z)P(y,z)))uQ(x,y,u)).
Застосування закону (xP(x))=
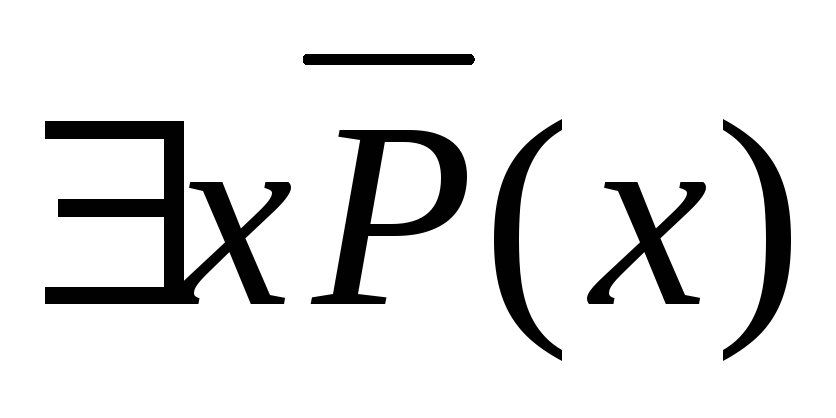 та закону де Моргана:
та закону де Моргана:
xy((zP(x,z)P(y,z)))uQ(x,y,u))=
xy(z![]() (x,z)
(x,z)![]() (y,z))uQ(x,y,u)).
(y,z))uQ(x,y,u)).
Використання законів логіки першого ступеня 6-7 та винесення квантора існування у префікс:
xy(z![]() (x,z)
(x,z)![]() (y,z))uQ(x,y,u))=
xyzu(
(y,z))uQ(x,y,u))=
xyzu(![]() (x,z)
(x,z)![]() (y,z)uQ(x,y,u)).
▲
(y,z)uQ(x,y,u)).
▲
8. Завдання до виконання
Формалізувати речення.
Я піду додому або залишуся тут і вип'ю чашку чаю, я не піду додому,отже я залишуся і вип'ю чашку чаю.
Якщо Олег ляже сьогодні пізно, він буде вранці в отупінні, якщо він ляже не пізно, то йому здаватиметься, що не варто жити, отже або Олег буде завтра в отупінні, або йому здаватиметься, що не варто жити.
Заперечення диз’юнкції двох висловлювань еквівалентно кон’юнкції заперечень кожного з цих висловлювань.
Якщо 2 – просте число, то це найменше просте число, якщо 2 – найменше просте число, то 1 не є прости числом; число 1 не є простим числом, отже 2 – просте число.
Ігор або втомився, або хворий, якщо він втомився, то він злий; він не злий, отже, він хворий.
Якщо завтра буде холодно, я одягну тепле пальто, якщо рукав буде полагоджений; завтра буде холодно, а рукав не буде полагоджений, отже, я не одягну тепле пальто.
Ні Північ, ні Південь не перемогли в громадянській війні.
Людину не підкуплять лестощі, якщо розум у людини є.
Іван прийде на іспит і він або Сергій отримає п’ятірку.
Якщо не можеш визнати похвали заслуженими, то вважай їх лестощами.
Побудувати таблицю істинності для висловлювань:
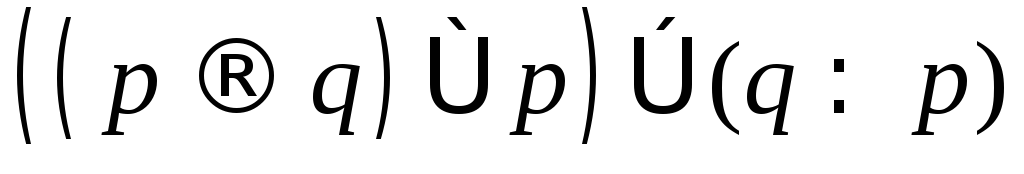 ;
;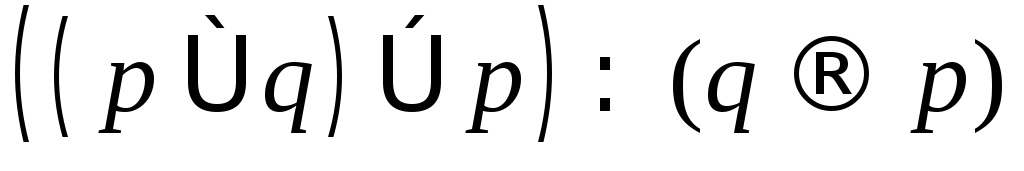 ;
;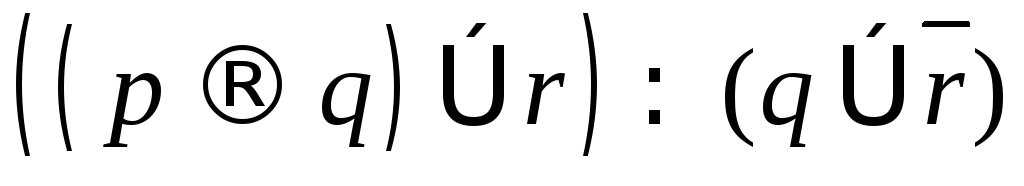 ;
;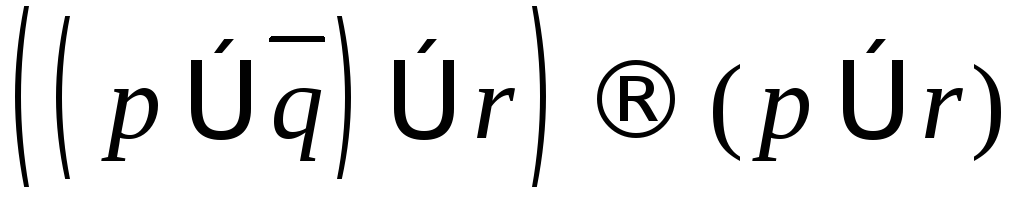 .
.
Побудовою таблиць істинності вияснити чи є тавтологіями висловлювання а – д:
 ;
; ;
;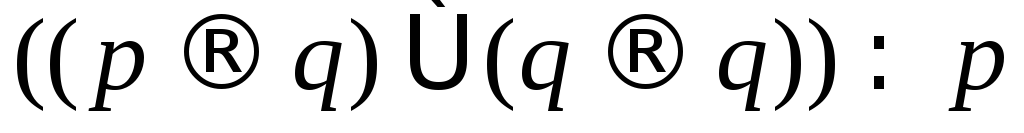 ;
;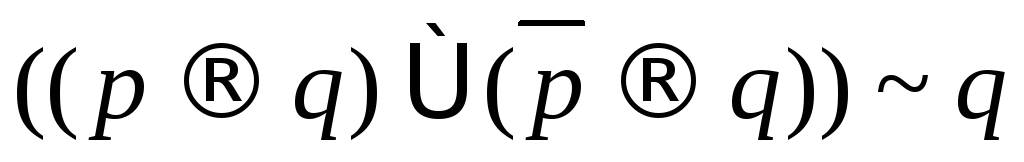 ;
;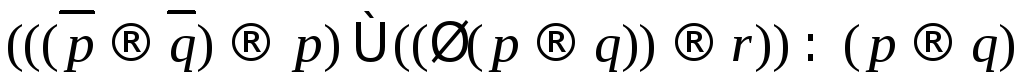 .
.
Побудовою таблиць істинності вияснити, чи є запереченням висловлювання а – д:
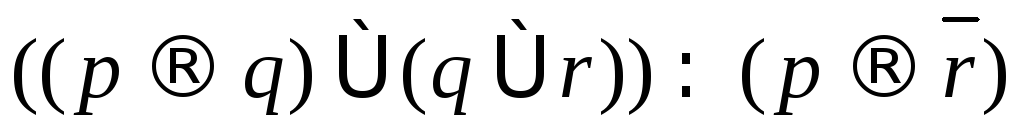 ;
;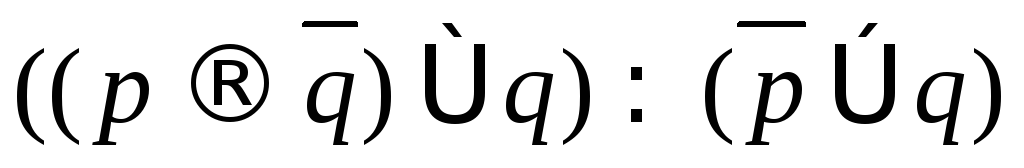 ;
;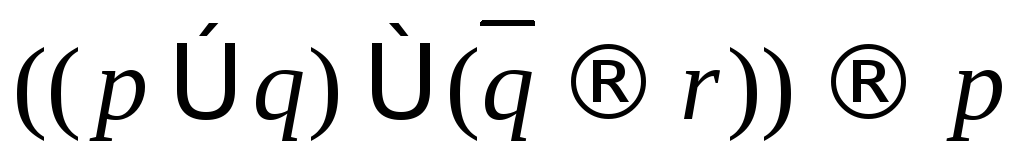 ;
;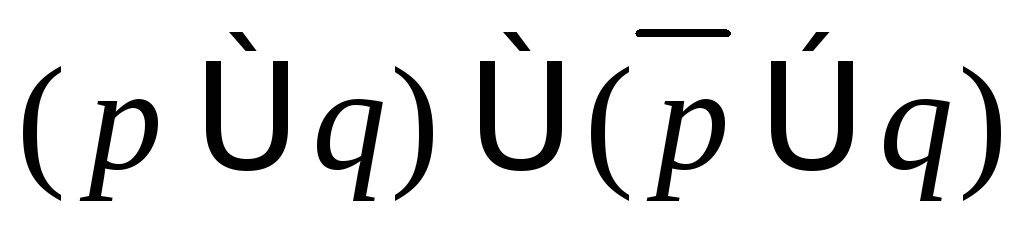 ;
;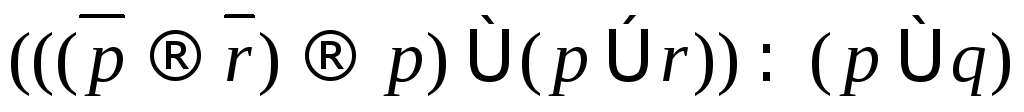 .
.
Еквівалентними перетвореннями перевірити, чи є тавтологіями висловлювання а – д:
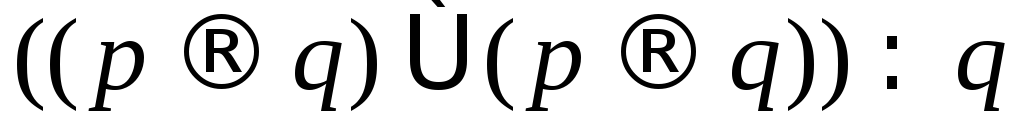 ;
;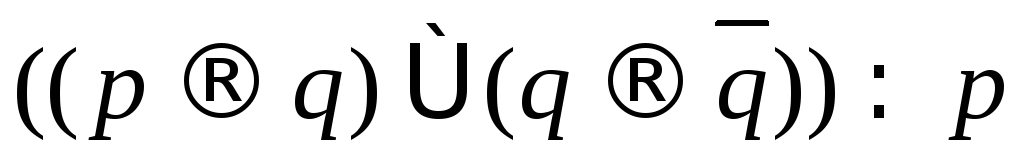 ;
;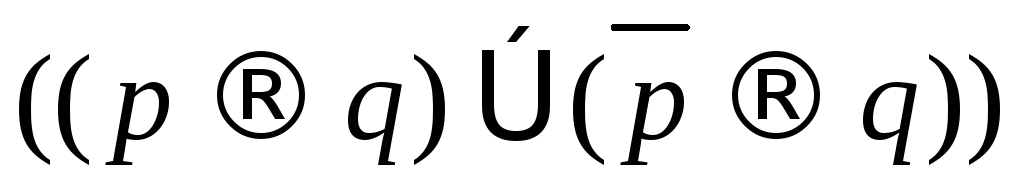 ;
;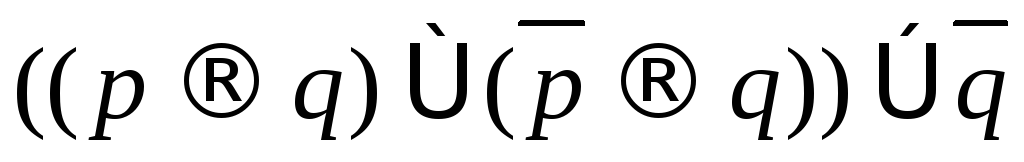 ;
;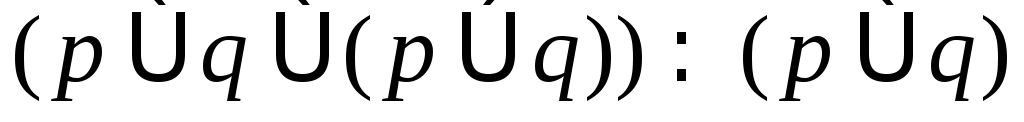 .
.
За означенням без побудови таблиць істинності та виконання еквівалентних перетворень перевірити, чи є тавтологіями висловлювання а – г:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() .
.
Використовуючи комбінований спосіб визначити, чи є тавтологіями формули а – д:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() ;
;
д)
![]() .
.
8. Які формули є тавтологіями(завжди істинні)?
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() ;
;
д)
![]() .
.
9. Які формули є еквівалентними до формули
![]() ?
?
a)
![]() ; б)
; б)![]() ;
;
в)
![]() ; г)
; г)![]() .
.
10. Які твердження істинні?
а) Формула
![]() еквівалентна формулі
еквівалентна формулі![]() .
.
б) Формула
![]() еквівалентна формулі
еквівалентна формулі![]() .
.
в) Формула
![]() еквівалентна формулі
еквівалентна формулі![]() .
.
11. Зобразити висловлювання
![]() виключно за допомогою операцій
виключно за допомогою операцій![]() і
і![]() .
.
12. Зобразити висловлювання
![]() виключно за допомогою операцій
виключно за допомогою операцій![]() і
і![]() .
.
13. Зобразити висловлювання
![]() виключно за допомогою операцій
виключно за допомогою операцій![]() і
і![]() .
.
Зобразити висловлювання
 виключно за допомогою операцій
виключно за допомогою операцій і
і .
.
15. Довести, що формули еквівалентні:
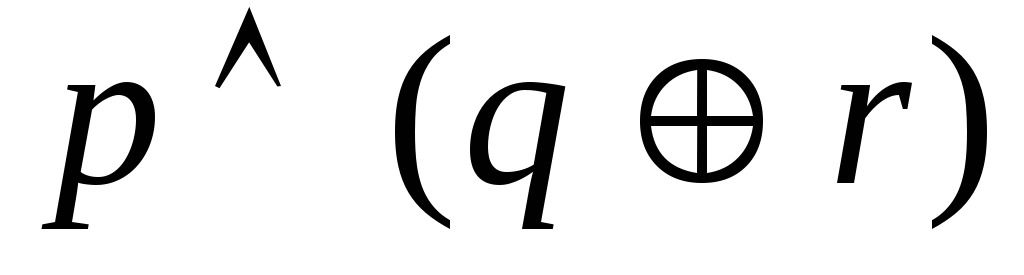 та
та ;
;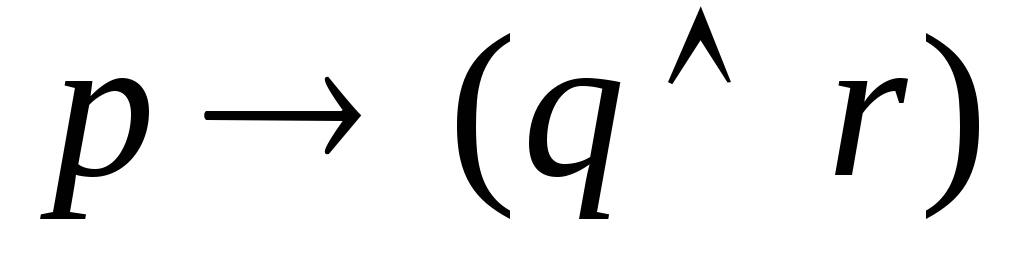 та
та ;
;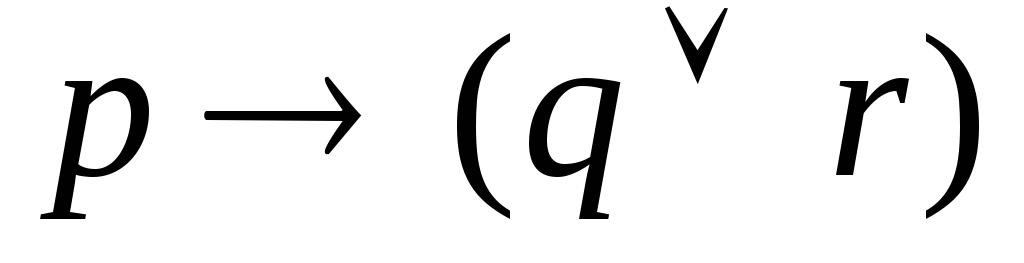 та
та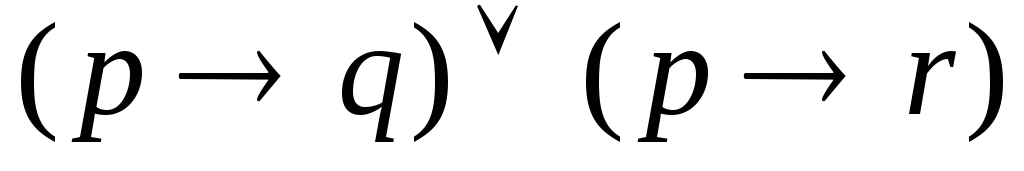 .
.
16. Перевірити, чи еквівалентні формули:
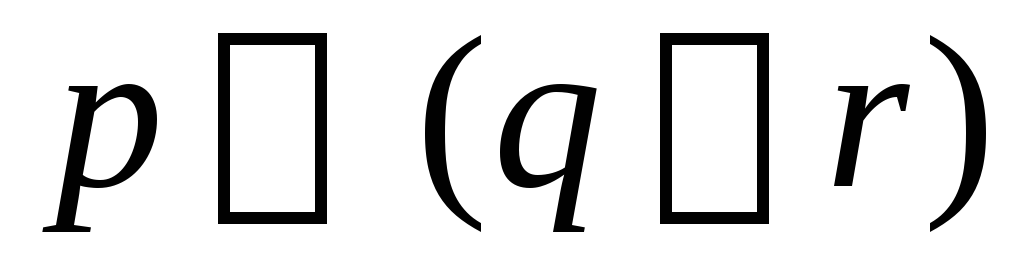 та
та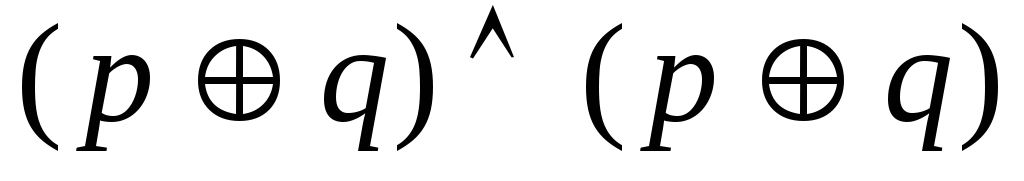 ;
;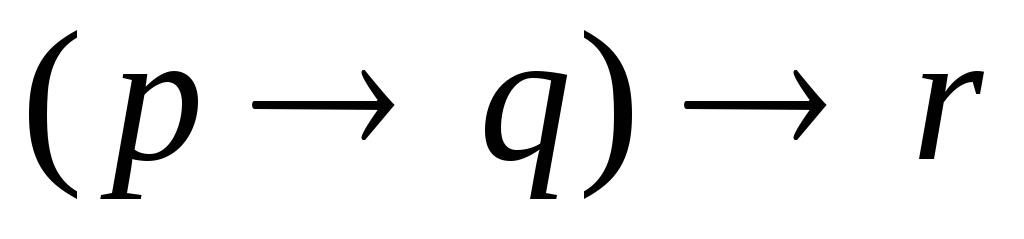 та
та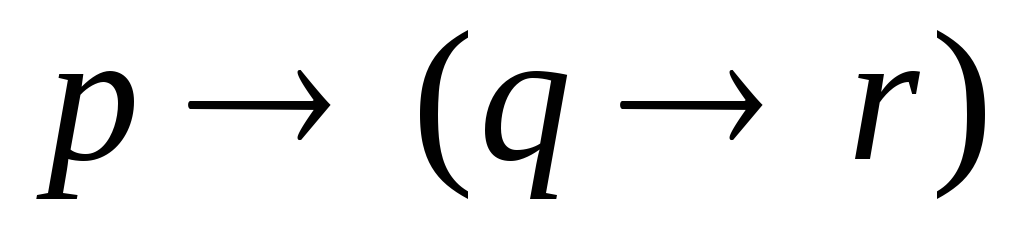 ;
;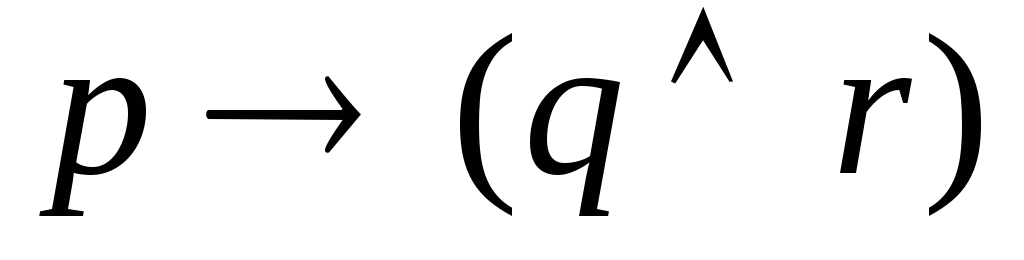 .
.
Зобразити висловлювання
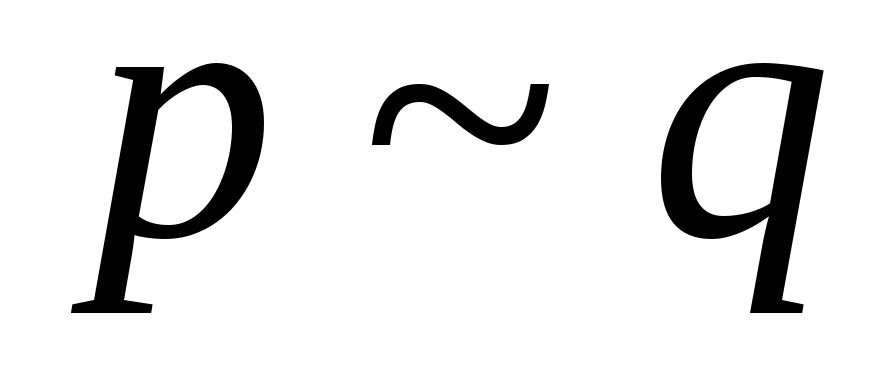 формулою над множиною логічних зв'язок
формулою над множиною логічних зв'язок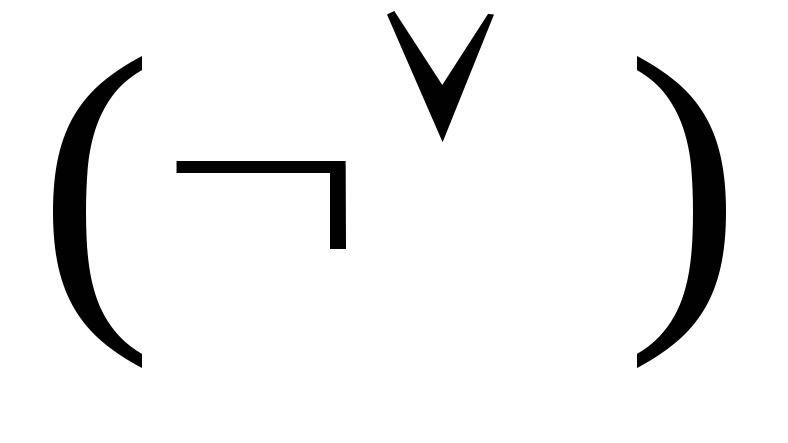 .
.
Зобразити висловлювання
 формулою над множиною логічних зв'язок
формулою над множиною логічних зв'язок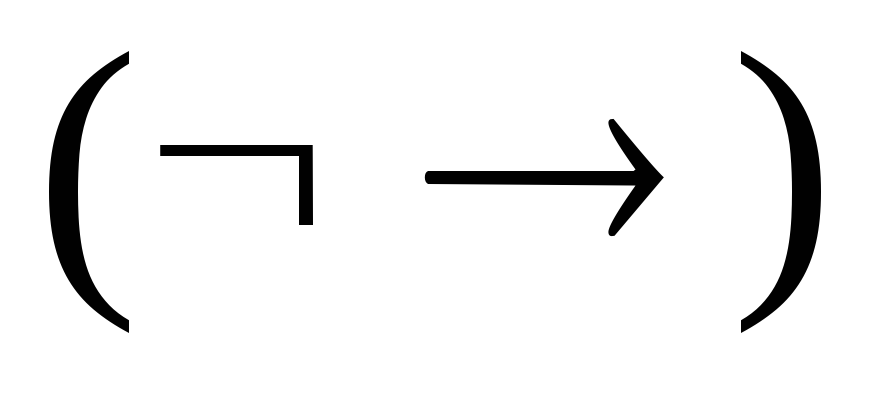 .
.
Який із законів дистрибутивності
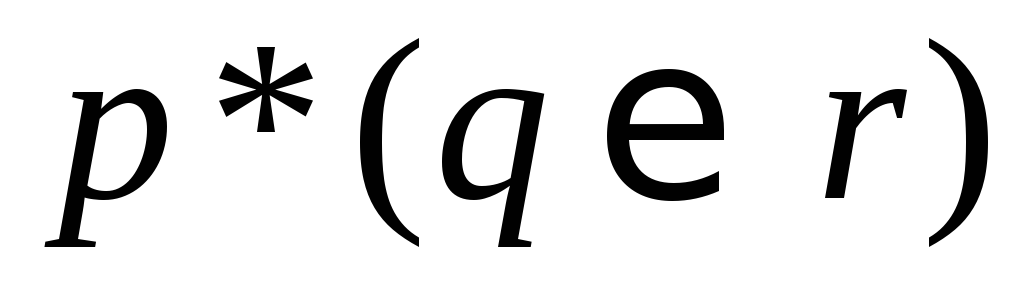 =
=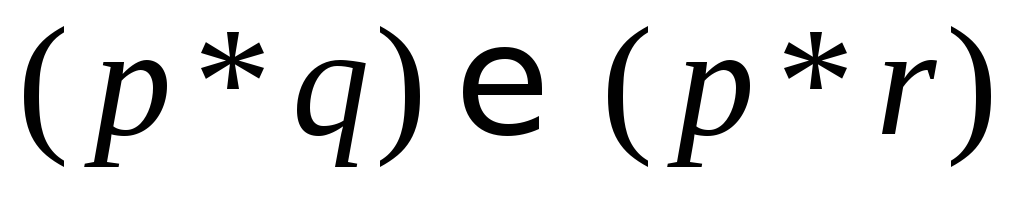 та
та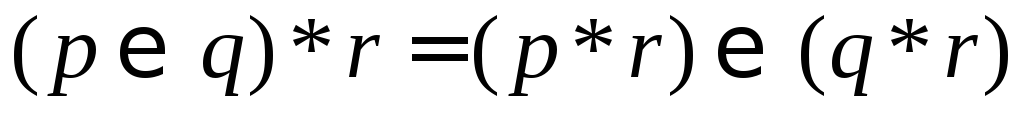 =
=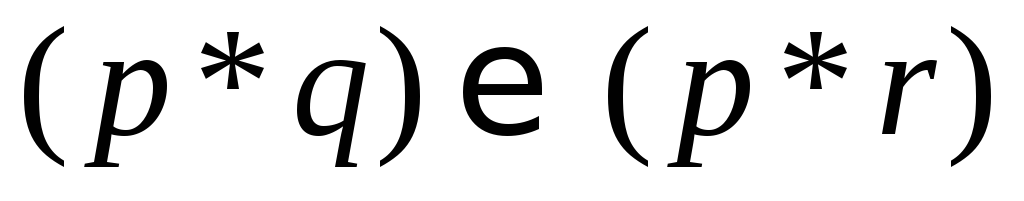 виконується, якщо замінити логічні
зв’язки, позначені символами «*» та
«
виконується, якщо замінити логічні
зв’язки, позначені символами «*» та
« »,
поданими у таблиці:
»,
поданими у таблиці:
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
* |
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
~ |
|
|
|
|
|
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
|
* |
|
|
|
|
|
~ |
~ |
~ |
~ |
|
|
~ |
|
|
|
~ |
|
|
|
|
Аналогічно із завданням 19 визначити, для яких логічних зв’язок виконуються закони:
а) асоціативності; б)комутативності;в) ідемпотентності,
д) поглинання;г) закони де Моргана.
Виведіть співвідношення для сталих для операцій імплікації, еквівалентності, альтернативного або.
Предикат
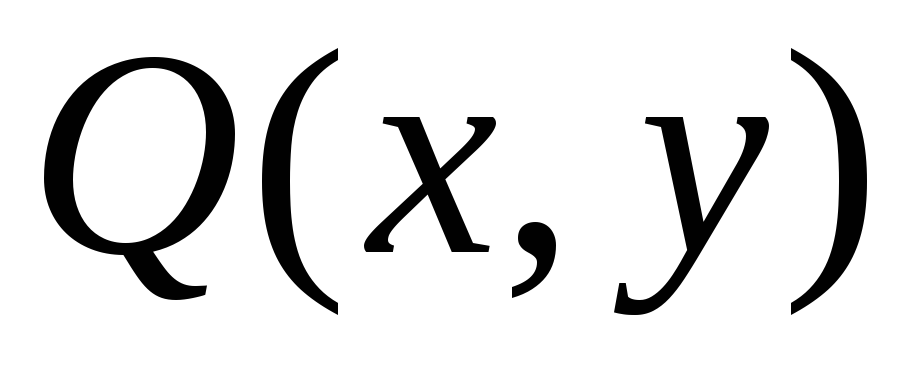 означаєx
= x-y.
Предметною областю кожної змінної
є множина цілих чисел. Знайти значення
істинності висловлювань:
означаєx
= x-y.
Предметною областю кожної змінної
є множина цілих чисел. Знайти значення
істинності висловлювань:
а) Q(1,1); б) Q(2,0);
в)![]() ; г)
; г)
![]() ;
;
д)
![]() ; е)
; е)![]() ;
;
є)
![]() ; ж)
; ж)![]() ;
;
з)
![]() ;
и)
;
и)![]() .
.
Предметною областю кожної змінної
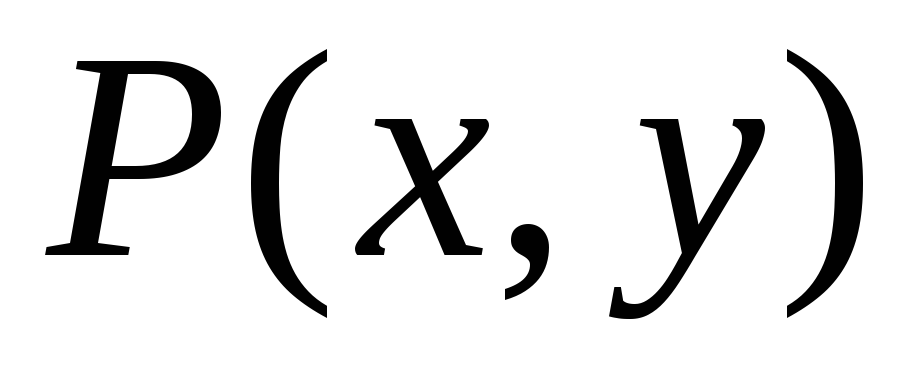 є
множина {1,2,3}. Записати висловлювання
логічних зв’язок кон'юнкції та
диз'юнкції:
є
множина {1,2,3}. Записати висловлювання
логічних зв’язок кон'юнкції та
диз'юнкції:
а)
![]() ; б)
; б)![]() ;
;
в)
![]() ; г)
; г)![]() ;
;
д)![]() ; е)
; е)![]() .
.
Предикат
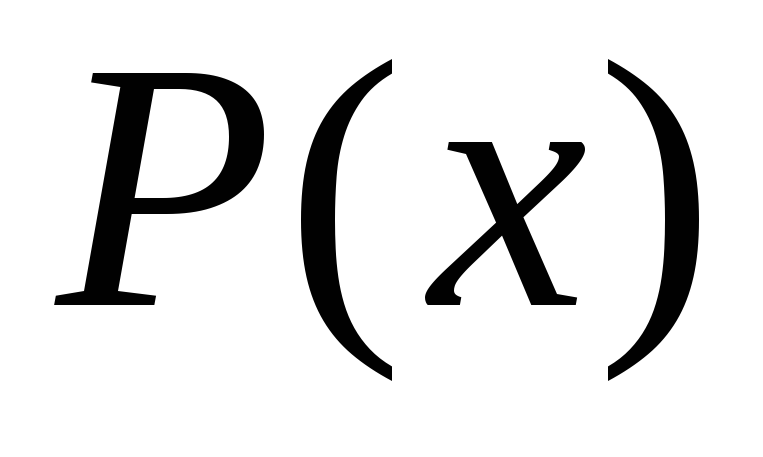 означає
означає
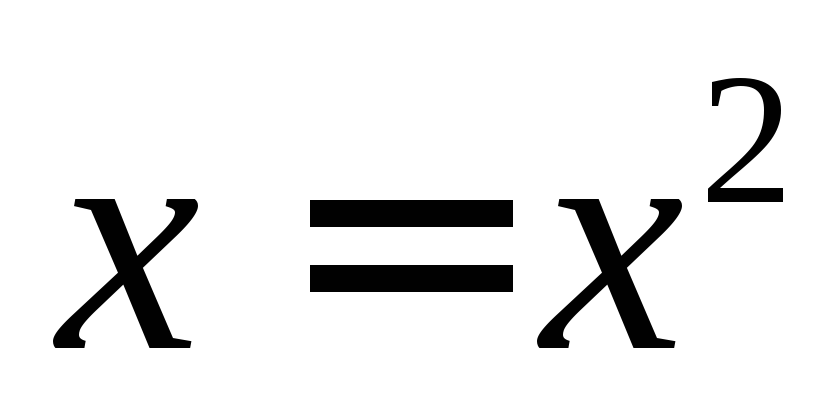 , а предметною областю змінної х є
множина цілих чисел. Знайти значення
істинності висловлювань а–д:
, а предметною областю змінної х є
множина цілих чисел. Знайти значення
істинності висловлювань а–д:
а) P(1); б) P(2);
в) P(0);
г) ![]() ;
;
д)
![]() .
.
Побудувати випереджену нормальну форму:
а)
![]() ;
;
б)
![]() .
.
Записати заперечення висловлювань а - г формулами логіки
першого ступеня. Записати отримані висловлювання словами:
а) кожний студент групи любить математику;
б) у групі є студент, який ніколи не бачив комп'ютера;
в) у групі є студент, який прослухав усі запропоновані математичні курси;
г) у групі є студент, який відвідав принаймні одну аудиторію кожного з навчальних корпусів університету.
Змінні хтаyнабувають значень із множини {0, 1, 2}. Записати формулу, еквівалентну до висловлювань, без використання кванторів:
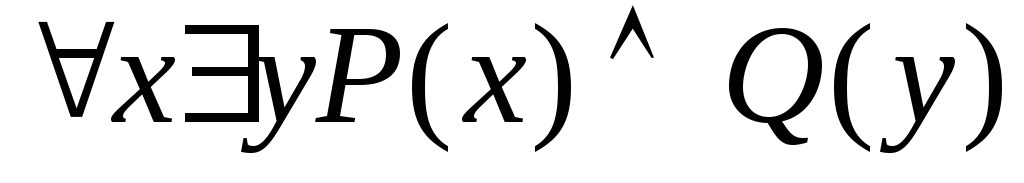 ;
;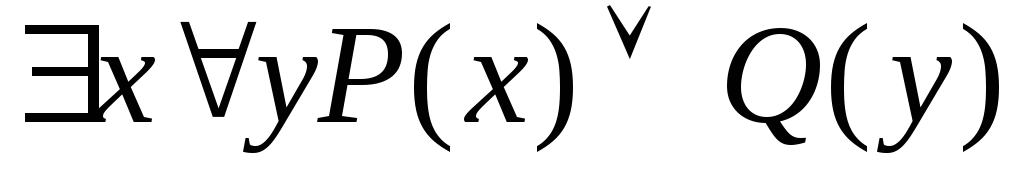 ;
;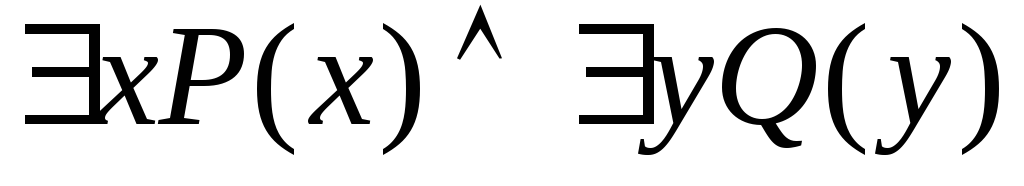 ;
;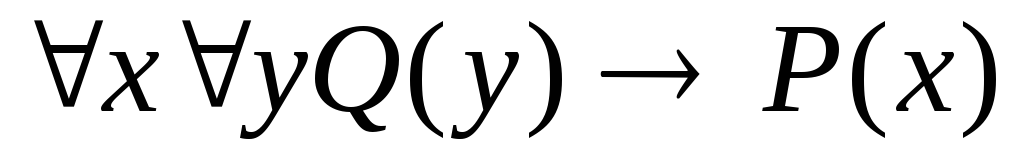 .
.
Позначення
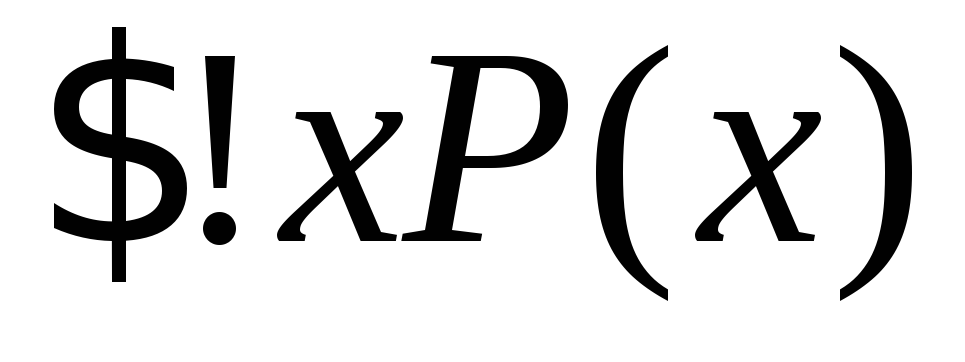 відповідає реченню "У предметній
області
відповідає реченню "У предметній
області
існує таке єдине х, що Р(х) істинне". Нехай множина цілих чисел є предметною областю змінноїх. Знайти значення істинності формул а - е:
а)
![]() ;
б)
;
б)![]() ;
;
в)
![]() ;
г)
;
г)![]() ;
;
д)
![]() ;
е)
;
е)![]() .
.
Здана предметна область М={1,2,3} змінної х. Записати висловлювання
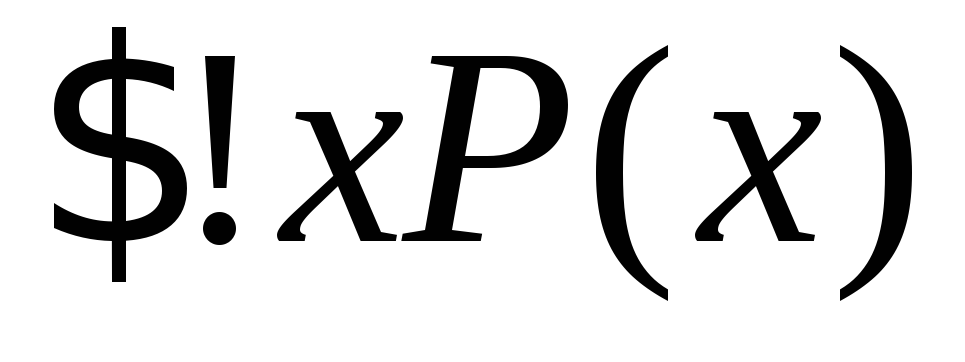 з допомогою заперечення, кон'юнкції
та диз'юнкції.
з допомогою заперечення, кон'юнкції
та диз'юнкції.
Записати формулу еквівалентну
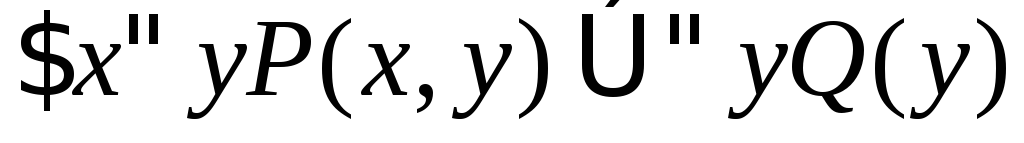 без використання квантора загальності.
без використання квантора загальності.
Змінні хтаyнабувають значень із множини {0, 1, 2}. Записати формулу без використання кванторів, еквівалентну до висловлювання:
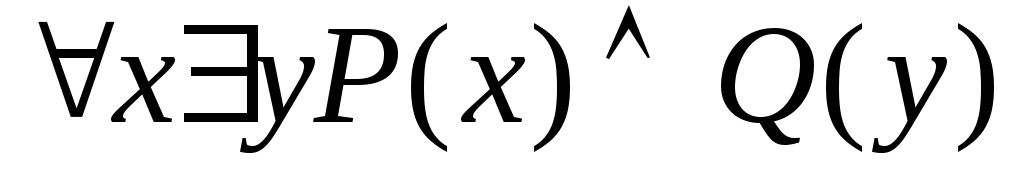 .
.
Змінні хтаyнабувають значень із множини {1,2,3}. Записати формулу без використання кванторів, еквівалентну до висловлювання:
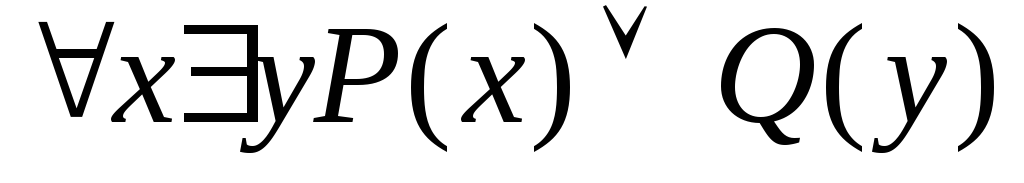 .
.
Змінні хтаyнабувають значень із множини {1,2,3}. Записати формулу без використання кванторів, еквівалентну до висловлювання:
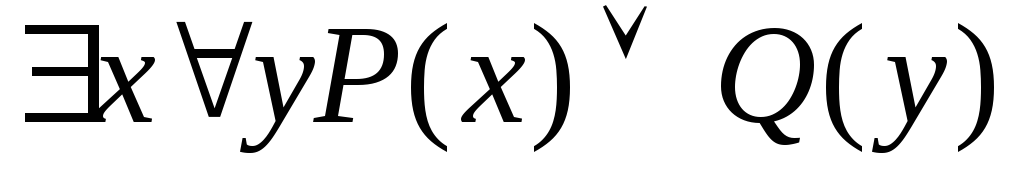 .
.
Записати формулу без використання квантору загальності, еквівалентну до висловлювання:
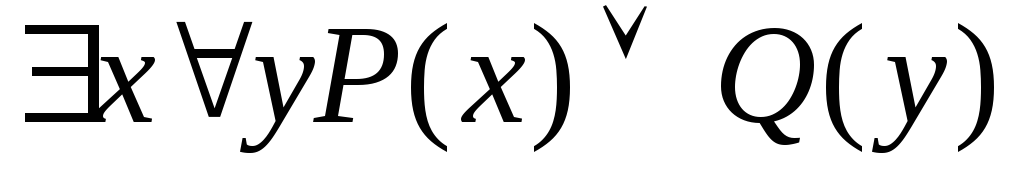 .
.
Записати формулу без використання квантору існування, еквівалентну до висловлювання:
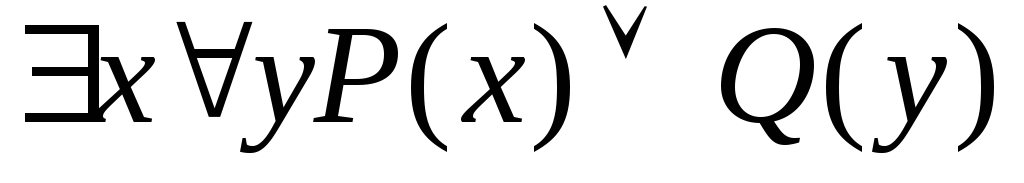 .
.
