2.3.Теорема Остроградського-Гауса та її застосування

Напруженість електростатичного поля зручно представити через густину силових ліній, що пронизують елементарну ділянку поверхні, розміщену перпендикулярно до цих ліній (рис.2.6 ).

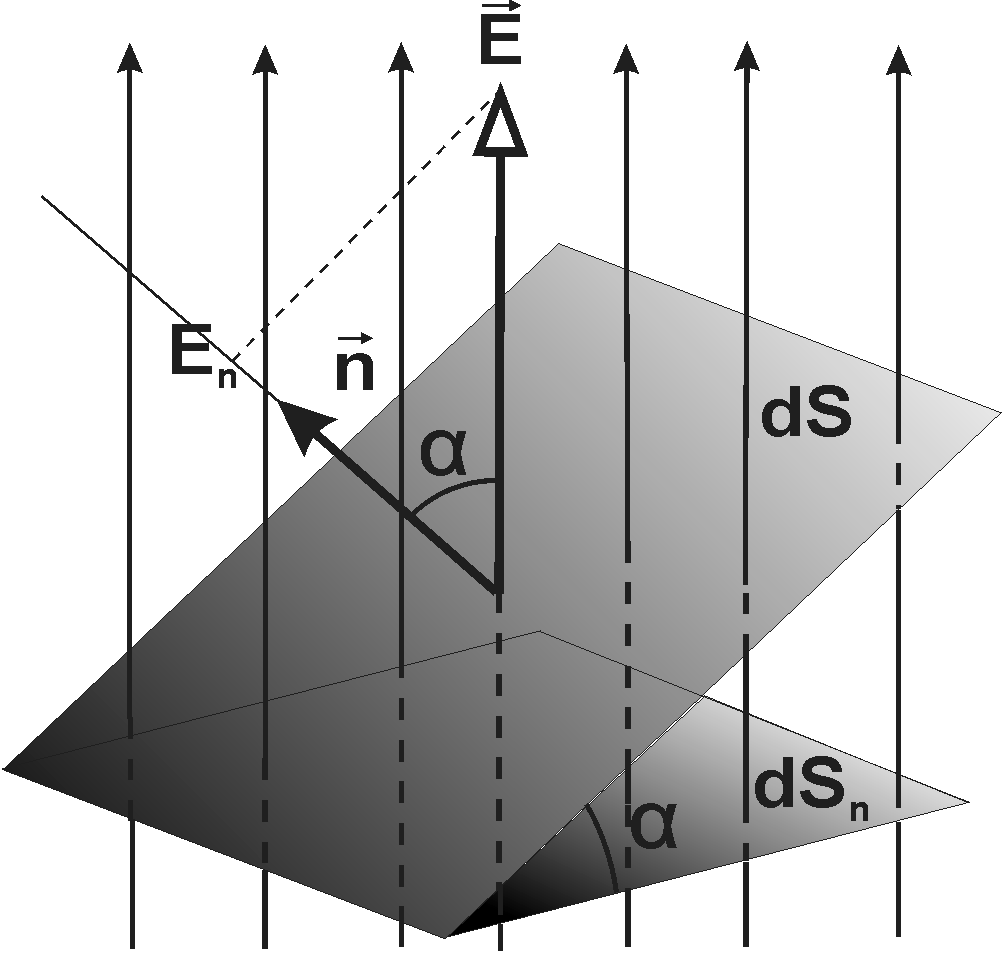
Рис. 6.

З останнього рівняння випливає:

(2.18)

Величину вектора dФ_Е називають потоком вектора напруженості через елементарну площадку dS. З рівняння (2.8) випливає, що потік вектора напруженості Ф_Е через поверхню S дорівнює:

Ф_Е= (2. 19)

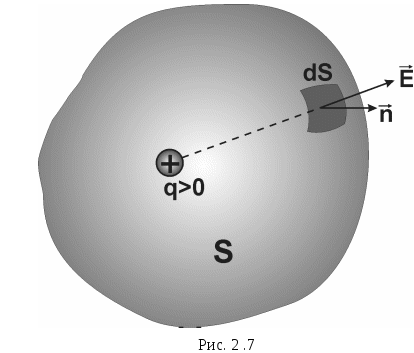
Згідно з теоремою Остроградського-Гауса, потік вектора напруженості електростатичного поля через довільну замкнену поверхнюS дорівнює алгебраїчній сумі зарядів, які обмежені цією поверхнею ( Рис.2.7 ), поділеній на електричну постійну ₀:

Рис. 2.8

(2.20)

Теорема Остроградського – Гауса використовується для розрахунку електростатичних полів, створених зарядженими тілами найрізноманітніших конфігурацій.

(2.20)

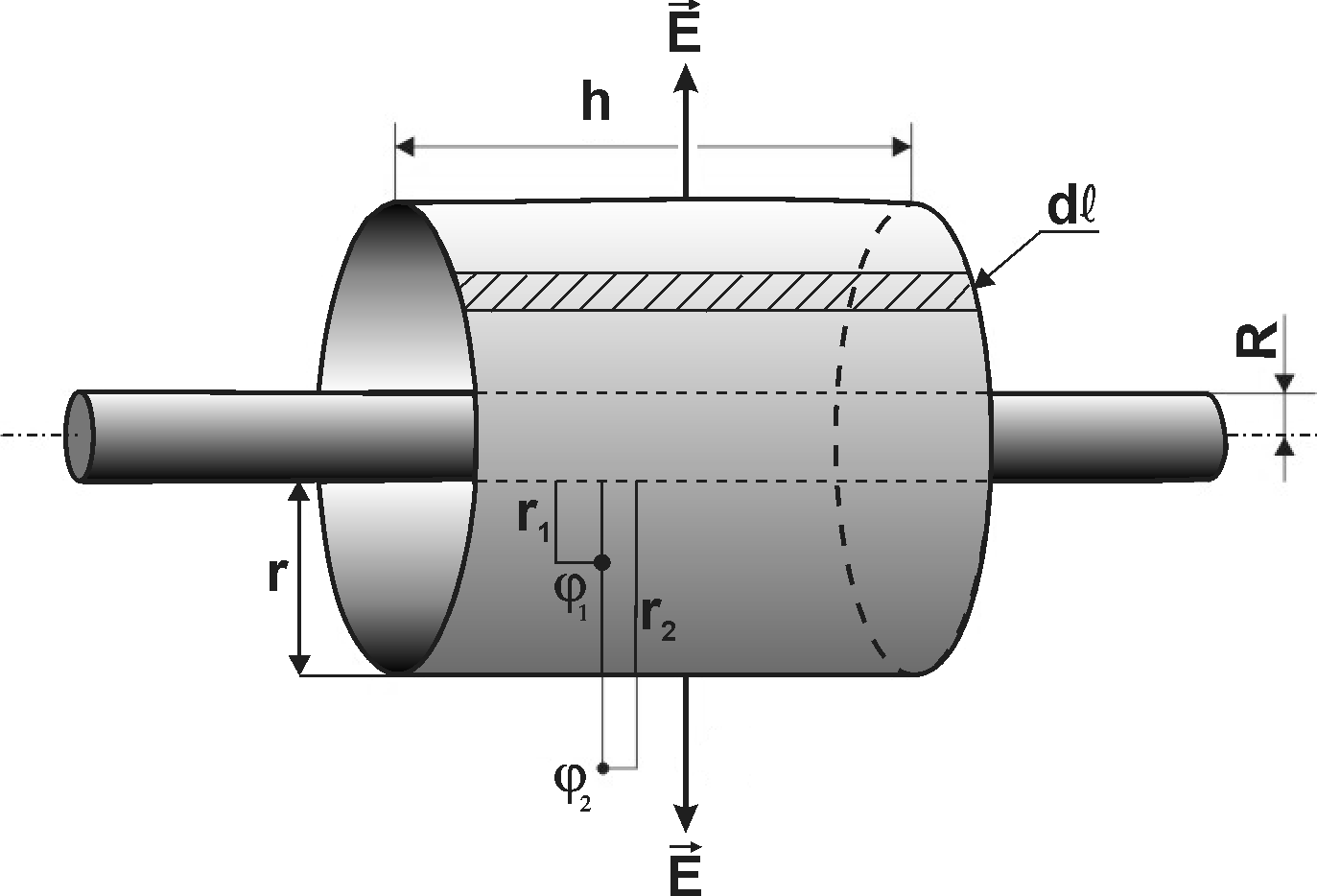
Розглянемо для прикладу, розрахунок електростатичного поля, створеного нескінченно довгим, рівномірно зарядженим циліндром з радіусом R і з лінійною густиною електричних зарядів (рис.2.8).

В ролі замкненої поверхні, що оточує цей циліндр, візьмемо коаксіальний циліндр радіусом r і висотою h. Повний потік вектора напруженості буде дорівнювати потоку тільки через бічну поверхню замкнутого циліндра, оскільки силові лінії електричного поля не перетинають площі основ цього циліндра (рис. 2.8).

. (2.21)

Враховуючи, що в нашому випадку E_n = E аотримаємо,або.Звідси

. (2.22)

Різниця потенціалів між двома точками, які знаходяться в одній площині на відстанях r₁ i r₂ від осі зарядженого циліндра, з (2.11):

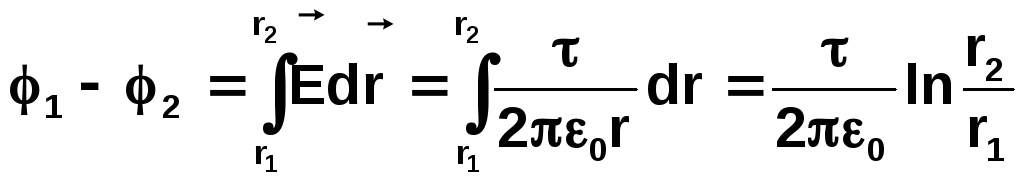. (2.23).

4. Електроємність провідника

Здатність провідника накопичувати електричні заряди характеризується фізичною величиною, яка називається його електроємністю. Електроємність провідника визначається його геометричними розмірами, діелектричною проникливістю середовища, в якому знаходиться цей провідник а також присутністю інших провідників. Електрична ємність відокремленого провідника ( провідника, розміщеного вдалині від інших провідників ) дорівнює відношенню величини заряду провідника до його потенціалу

. (2.24)

Електроємністю відокремленого провідника називається фізична величина, яка вимірюється зарядом, потрібним для зміни його потенціалу на одиницю. Електроємність відокремленої кулі:

,

де R – радіус кулі; ε– діелектрична проникливість середовища, в якому знаходиться куля. Електрична ємність навіть досить габаритних провідників є незначною. Крім цього на її величину впливають сторонні тіла. Тому для одержання великих електроємностей в малих об’ємах широко використовуються електричні прилади, що називаються конденсаторами. Найпростішим варіантом конденсатора є відповідної форми два провідники – обкладки, розділені шаром діелектрику. Електричне поле конденсатора повністю локалізоване між його обкладками і тому на нього не впливають зовнішні поля. На обкладки подаються рівні за величиною і протилежні за знаком електричні заряди.

Електрична ємність конденсатора визначається за формулою

,

де q – величина заряду на одній з обкладинок конденсатора; U–різниця потенціалів між обкладками. Якщо обкладками є дві металеві пластинки, між якими знаходиться тонкий шар діелектрика, то такий конденсатор називається плоским.

На основі теореми Остроградського-Гауса можна легко довести, що ємність плоского конденсатора дорівнює:

, (2.25)

де ₀ – електрична стала, ₀=8,85^.10^-12 Ф/м;

 - відносна діелектрична проникливість середовища, що розділяє пластини конденсатора; d – віддаль між пластинами.

2.5 Заряджання і розряджання конденсатора.

Заряджання і розряджання конденсатора пов’язанні зі зміною величини заряду на його обкладинках. Під час заряджання і розряджання конденсатора через опір ( Рис.2.9) зміна заряду на обкладинках і різниці потенціалів між ними відбувається не миттєво, а за певний скінчений проміжок часу.

Розглянемо процеси заряджання і розряджання конденсатора через опір і виведемо відповідні формули, які встановлюють залежність цих процесів від параметрів електричного кола .

Заряджання конденсатора.

Рис.2.9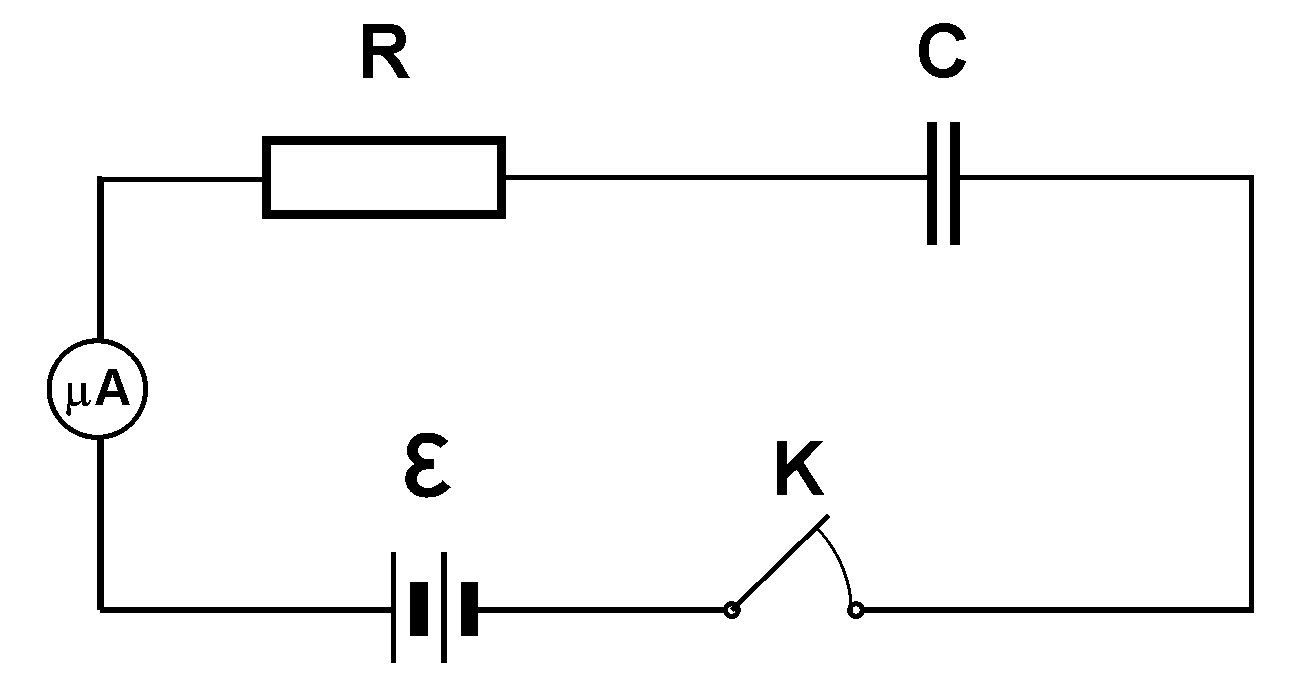

Розглянемо електричне коло показане на рис.2.9. Воно містить конденсатор з ємністю С, резистор з опором R і джерело постійного струму з Е.Р.С. . Будемо вважати, що до моменту вмикання ключа, конденсатор не заряджений. При вмиканні ключаК в колі з'явиться струм, спричинений заряджанням конденсатора. При нагромадженні заряду на обкладинках конденсатора , між ними виникне різниця потенціалів

,

яка з плином часу буде наростати. Встановимо закон зміни різниці потенціалів від часу при зарядці конденсатора. Застосуємо закон Ома

ε (2.26)

для електричного кола , показаного на рис.1, при замкнутому ключі К. Оскільки , то

. (2.27)

З рівнянь (2.26) і (2.27) отримаємо диференціальне рівняння

. (2.28)

Розділивши в цьому рівнянні змінні

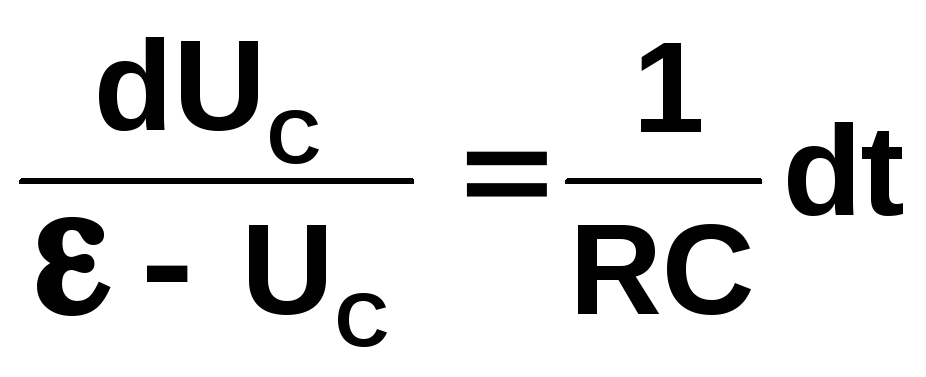(2.29)

і проінтегрувавши його, отримаємо:

.

З початкових умов , визначимо постійну інтегрування . Тоді

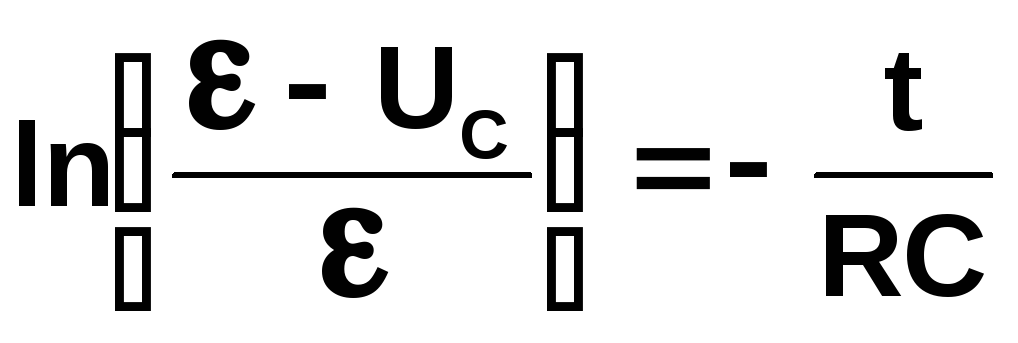. (2.30)

Після потенціювання цього виразу отримаємо

. (2.31)

Звідси видно, що при , а при напруга на конденсаторі асимптотично наближається до Е.Р.С. джерела. Підставивши вираз (2.31) у (2.26), отримаємо залежність струму заряджання від часу

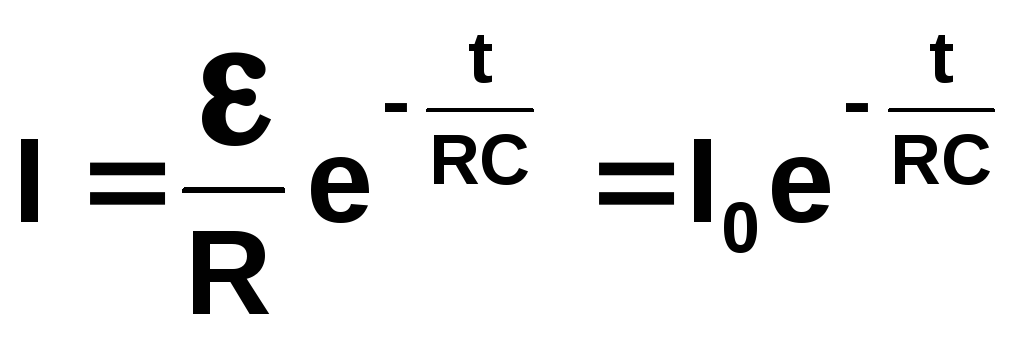. (2.32)

З рівняння (2.32) видно, що максимальне значення струм заряджання має в початковий момент часу і з плином часу воно зменшується, асимптотично наближаючись до нуля.

Використавши співвідношення (2.31) і (2.32), отримаємо закон зміни заряду на конденсаторі під час заряджання:

(2.33)

Заряджання конденсатора.

Нехай конденсатор з ємністю С заряджений до різниці потенціалів . Здійснимо розряджання через опірR, так як це показано на рис.2.10.

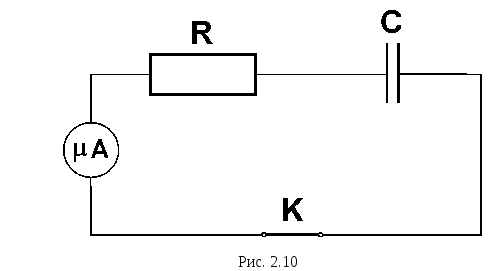
Закон Ома при розряджанні конденсатора запишемо у вигляді

. (2.34)

Враховуючи (2.27), запишемо

. (2.35)

Розділимо змінні в цьому диференціальному рівнянні

і після його інтегрування отримаємо:

. (2.36)

З початкових умов , , отримаємо, що .

В результаті рівняння (2.36) набере вигляду

і після його потенціювання

. (2.37)

В процесі розряджання конденсатора напруга на ньому зменшується і асимптотично наближається до нуля. Поділивши обидві частини рівняння (2.37) на величину опору R, згідно з (2.34), отримаємо:

, (2.38)

де початкове значення сили струму.

Оскільки , то з врахуванням (2.37) а також (2.38) отримаємо закон зміни заряду конденсатора при розряджанні:

(2.39)

З формули (2.39) видно, що при

, (2.40)

де .

Час , протягом якого заряд зменшується ве = 2,71 разів, називається часом релаксації. Отже час релаксації в електричному колі, що містить ємність С і опір R

. (2.41)

Час релаксації можна визначити графічним методом. З виразу (2.38) і (2.39) отримаємо

. (2.42)

При

.

Час релаксації можна визначити з графічної залежності , яка згідно з формулою (2.42) є лінійною залежністю від часу t ( Рис. 2.11.).

Згідно з цією залежністю, час релаксації дорівнює абсцисі точки на прямій ( Рис.2.11), для якої .

Рис. 2.11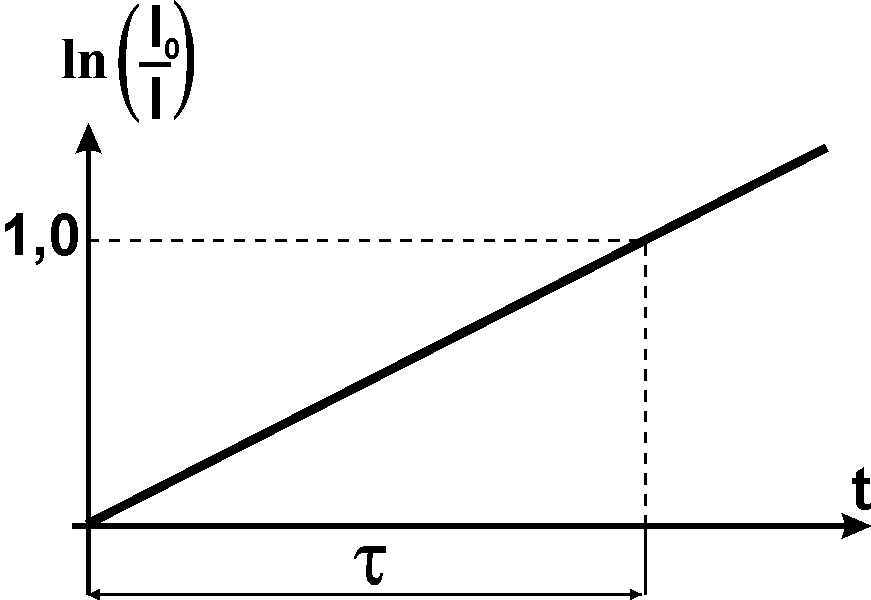

Енергія зарядженого конденсатора може бути записана такими формулами:

. (2.43)

Об’ємна густина енергії електричного поля зарядженого конденсатора

. (2.44)