14)Продовження

, (3.167)

де і– опір і питомий опір при температурі,– температурний коефіцієнт опору,– температура по шкалі Цельсія.

Рис.3.27

При температурі близькій до абсолютного нуля опір деяких провідників стає рівним нулю. Це явище називається надпровідністю. Воно було відкрите Камерлінг-Онессом у 1911 р. Якщо в замкнутому колі складеному з надпровідника, створити електричний струм, то він циркулюватиме тривалий час практично не зменшуючись протягом тижнів і місяців.

Виділимо в провіднику елементарний циліндр довжиною і площею поперечного перерізу. Нехай до циліндра прикладена різниця потенціаліві по ньому тече струм силою( рис. 3.27 )

Тоді формули (3.162) і (3.164) наберуть вигляду

. (3.168)

. (3.169)

Підставимо (3.169) в (3.168) і використаємо (3.158), дістанемо

. (3.170)

Врахуємо, що

. (3.171)

Підставимо (3.171) у вираз (3.170):

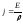; . (3.172)

Формули (3.172) можна представити також у векторній формі

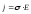; . (3.173)

Формули (3.173) – це закон Ома в диференціальній формі для однорідної ділянки кола.

В ізотропному провіднику носії струму в кожній точці рухаються в напрямку вектора . Закон Ома в диференціальній формі зв’язує густину струму в кожній точці всередині провідника з напруженістю електричного поля в тій самій точці.

Оскільки напрямлений рух носіїв струму створюється електричним полем в провіднику, то можна вважати, що середня швидкість напрямленого руху зарядів прямо пропорційна до напруженості поля в провіднику

, (3.174)

де коефіцієнт пропорційності називаєтьсярухливістю носіїв струму. Рухливість носіїв струму чисельно рівна швидкості їх напрямленого руху, якої вони набувають в провіднику під дією електричного поля з одиничною напруженістю.

Виразимо силу і густину струму через середню швидкість впорядкованого руху носіїв струму в провіднику. За часчерез поперечний переріз провідникапереноситься заряд

, (3.175)

де – концентрація носіїв струму,– заряд носія струму. Сила струму рівна

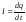; . (3.176)

Підставимо вираз (3.176) у формулу (3.159) отримаємо формулу густини струму

. (3.177)

Підставимо вираз (3.174) у формулу (3.177), дістанемо

. (3.178)

Порівняємо формулу (3.178) із виразом (3.172). Отримаємо формулу питомої електропровідності речовини

. (3.179)

Отже, питома електропровідність провідника прямо пропорційна електричному зарядові носія струму, рухливості носіїв і їх концентрації.

15)Робота і потужність струму. Закон Джоуля-Ленца

Розглянемо ділянку кола опором R до якої прикладена напруга U і по якій тече струм силою І. Із означення електричної напруги (3.160) визначимо елементарну роботу по переміщенню по колу елементарного заряду dq

. (3.211)

Із означення сили струму (3.156) визначимо елементарний заряд

. (3.212)

Підставимо вираз (3.212) у формулу (3.211)

. (3.213)

Проінтегруємо вираз (3.203) і отримаємо формулу роботи електричного струму

. (3.214)

У випадку постійного струму, коли ,, робота електричного струму визначається за формулою

. (3.215)

Потужність рівна роботі виконаній за одиницю часу

. (3.216)

Підставимо (3.213) у формулу (3.216). Отримаємо формулу потужності струму

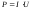. (3.217)

Якщо електричний струм не виконує роботу проти зовнішніх сил і не змінюється внутрішня енергія провідника то, як випливає з першого закону термодинаміки, робота струму рівна кількості теплоти, яка виділяється в провіднику

. (3.218)

З закону Ома для ділянки кола випливає

. (3.219)

Підставимо (3.219) у формулу (3.218)

. (3.220)

У випадку постійного струму формула (3.220) набере вигляду

. (3.221)

Формули (3.220) і (3.221) – це закон Джоуля-Ленца в інтегральній формі: кількість теплоти, яка виділяється в провіднику при проходженні електричного струму, прямо пропорційна квадрату сили струму, опору провідника і часу проходження струму

Розглянемо циліндричний провідник з площею поперечного перерізу , довжиною, по якому тече струм силою. Тоді за часв ньому виділиться кількість теплоти, яка згідно з формулою (3.221) рівна

. (3.222)

З формул (3.164) і (3.159) отримаємо

; . (3.223)

Підставимо (3.223) у формулу (3.222)

(3.224)

де – об’єм провідника.

Питомою тепловою потужністю струму називається фізична величина, рівна кількості теплоти, яка виділяється в одиниці об’єму провідника за одиницю часу

. (3.225)

Підставимо (3.224) у формулу (3.225) отримаємо

. (3.226)

Формула (3.226) – це закон Джоуля-Ленца в диференціальній формі: питома теплова потужність струму прямо пропорційна питомому опору провідника і квадратові густини струму.

Використовуючи формули (3.173) вираз (3.226) можне бути представлений у вигляді

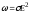. (3.227)

Формули (3.227) – це другий варіант закону Джоуля-Ленца в диференціальній формі: питома теплова потужність струму прямо пропорційна питомій електропровідності провідника і квадрату напруженості електричного поля.