6) Електричне поле нескінченної рівномірно зарядженої площини.

Розглянемо нескінченну площину рівномірно заряджену електричним зарядом з поверхневою густиною заряду:

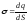. (3.49)

Поверхневою густиною електричного заряду називається фізична величина рівна електричному зарядові одиниці площі поверхні по якій розподілений заряд. У випадку рівномірного розподілу електричного заряду q по поверхні S поверхнева густина заряду рівна:

. (3.50)

Рис.3.9

В якості замкненої поверхні виберемо циліндричну поверхню з площею основи вісь якої перпендикулярна до зарядженої площини, як зображено на рис.3.9.

Застосуємо теорему Остроградського-Гауса

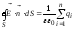. (3.51)

Інтеграл по замкненій поверхні S запишемо як суму трьох інтегралів. Сумарний заряд, який охоплений поверхнею S рівний зарядові круга площею S_осн., який вирізує циліндр S на зарядженій площині. Виходячи із формули (3.50), цей заряд рівний

(3.52)

Підставимо (3.52) в (3.51):

Оскільки і, то

. (3.53)

Інтеграли по поверхнях основ рівні:

(3.54)

Підставимо (3.54) в (3.53):

. (3.55)

Із формули (3.55) випливає, що напруженість електричного поля, створеного нескінченною рівномірно зарядженою площиною не залежить від відстані до площини, тобто є однаковою в усіх точках простору по обидва боки від зарядженої площини. Це електричне поле є однорідним. Його силові лінії перпендикулярні до зарядженої площини.

7)Робота сил електричного поля. Теорема про циркуляцію вектора напруженості електричного поля. Потенціал

Нехай електричний заряд здійснює елементарне переміщенняпід дією силиелектричного поля напруженістю, як зображено на рис. 3.10. Тоді виконана полем елементарна робота рівна

Рис.3.10

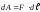. (3.56)

Запишемо формулу напруженості електричного поля

Визначимо з цієї формули силу (3.58)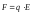

Підставимо вираз (3.58) у формулу (3.56) або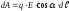

. (3.60)

Проінтегрувавши вираз (3.59), одержимо формулу роботи при переміщенні електричного заряду в електричному полі з напруженістювздовж траєкторії

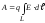. (3.61)

Нехай точковий електричний заряд здійснює переміщення в полі іншого точкового електричного заряду, тоді модуль напруженості електричного поля створеного зарядомрівний

. (3.62)

З рисунка одержимо

. (3.63)

Підставимо (3.62) і (3.63) у вираз (3.60)

.

Проінтегруємо цей вираз

. (3.64)

Отже робота сил електричного поля не залежить від форми траєкторії, а залежить лише від положення початкової і кінцевої точки. Тому електростатичне поле є потенціальним. При переміщенні електричного заряду по замкненій траєкторії точки 1 і 2 будуть співпадати тому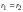. При цій умові, як випливає із формули (3.64) робота буде дорівнювати нулеві. Тоді формула (3.61) набере вигляду

. (3.65)

Інтеграл по замкнутому контуру від скалярного добутку вектора напруженості електричного поляна елементарний вектор довжини контуруназиваєтьсяциркуляцією вектора напруженості електричного поля. Співвідношення (3.10) – це теорема про циркуляцію вектора напруженості електричного поля: циркуляція вектора напруженості електростатичного поля по замкнутому контуру рівна нулю.

Робота потенціальних сил рівна зміні потенціальної енергії з протилежним знаком

. (3.66)

З порівняння формул (3.64) і (3.65) можна одержати формулу потенціальної енергії взаємодії двох точкових зарядів:

. (3.67)

Для характеристики потенціального поля можна використати поняття потенціалу.

Потенціалом електричного поля називається скалярна фізична величина рівна потенціальній енергії одиничного позитивного точкового заряду вміщеного в дану точку поля

Рис.3.11

. (3.68)

Одиницею вимірювання потенціалу в системі одиниць є вольт. 1В – це потенціал такої точки поля, в якій точковий позитивний заряд величиною 1Кл має потенціальну енергію 1Дж.

Підставивши вираз (3.67) в (3.68) отримаємо формулу потенціалу точкового заряду

. (3.69)

На рис.3.11.зображено залежність потенціалу точкового електричного заряду від відстані графічно.

Продиференціюємо вираз (3.68)

. (3.70)

Оскільки , то