3)Розрахунок електричних полів за допомогою теореми Остроградського-Гауса

Для розрахунку електричного поля створеного зарядженим тілом необхідно розбити це тіло на точкові заряди і визначити напруженість електричного поля в деякій точці простору за принципом суперпозиції. Для багатьох тіл такі розрахунки математично досить складні. Для деяких симетричних тіл розрахунок електричного поля значно спрощується при використанні теореми Остроградського-Гауса. Розглянемо деякі приклади таких розрахунків.

а) Електричне поле рівномірно зарядженої кулі.

Розглянемо кулю радіусом R рівномірно заряджену по об’єму з об’ємною густиною заряду

. (3.27)

Для рівномірного розподілу заряду можна вважати що

. (3.28)

Оскільки об’єм кулі рівний

, (3.29)

то підставивши (3.29) в (3.28) одержимо:

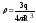. (3.30)

Виберемо замкнену поверхню S у формі сфери радіусом r, центр якої співпадає з центром зарядженої кулі, як зображено на рис. 3.5. Розглянемо випадок коли , тобто визначимо напруженість електричного поля всередині зарядженої кулі. Запишемо теорему Остроградського-Гауса для випадку неперервного розподілу електричного заряду.

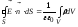(3.31)

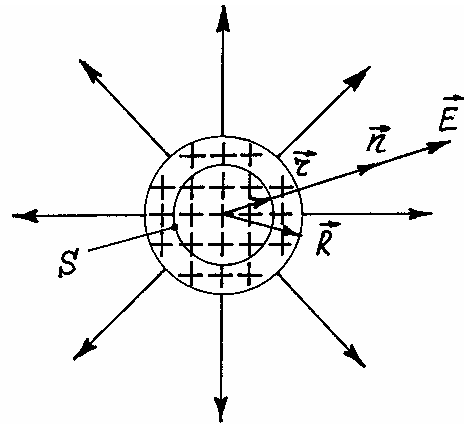
Рис.3.5

або

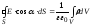(3.32)

В даному випадку і, тому

. (3.33)

Виходячи з міркувань симетрії випливає, що величина Е за модулем постійна у всіх точках сферичної поверхні S, тому винесемо Е за знак інтегралу:

. (3.34)

У формулі (3.34) інтеграл по замкненій поверхні рівний площі сферичної поверхні радіусом r а інтеграл по об’єму V рівний об’єму цієї ж сферичної поверхні, тому

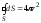, (3.35)

. (3.36)

Підставимо вирази (3.30), (3.35) і (3.36) у формулу (3.34):

. (3.37)

Отже всередині рівномірно зарядженої по об’єму кулі напруженість електричного поля прямо пропорційна відстані від центру кулі до даної точки.

Рис.3.6

4)Розглянемо випадок коли , тобто визначимо напруженість електричного поля ззовні зарядженої кулі (рис. 3.6). Запишемо теорему Остроградського-Гауса.

(3.38)

або

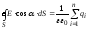. (3.39)

Оскільки вектори імають однаковий напрямок то. Виходячи з міркувань симетрії можна стверджувати, що модульЕ однаковий в усіх точках поверхні S. Врахуємо також, що поверхня S охоплює кулю з зарядом q, тоді вираз (3.39) набере вигляду:

. (3.40)

Підставимо (3.35) в (3.40):

. (3.41)

Із формули (3.41) випливає, що ззовні зарядженої кулі напруженість електричного поля, так само як і для точкового заряду, обернено пропорційна квадратові відстані від центру кулі до даної точки простору.

Рис.3.7.

На рис. 3.7 зображено залежність напруженості електричного поля Е від відстані r .

5) Електричне поле нескінченої рівномірно зарядженої прямої.

Розглянемо нескінченно довгу пряму, рівномірно заряджену електричним зарядом з лінійною густиною заряду .

Рис.3.8.

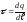. (3.42)

Лінійною густиною електричного заряду називається фізична величина рівна електричному зарядові одиниці довжини лінії вздовж якої він розподілений. У випадку рівномірного розподілу електричного заряду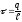

(3.43)

де – електричний заряд який розподілений вздовж лінії довжиною.

В якості замкненої поверхні виберемо циліндричну поверхню радіусом r, висотою , вісь якої співпадає із зарядженою прямою, як зображено на рис. 3.8. Застосуємо теорему Остроградського-Гауса:

. (3.44)

Інтеграл по замкненій поверхні S запишемо як суму трьох інтегралів: по бічній поверхні, по першій і другій основах. Сумарний заряд, який охоплений поверхнею S, рівний зарядові на ділянці прямої довжиною . Із формули (3.43) цей заряд рівний: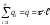

. (3.45)

Підставимо (3.45) в (3.44):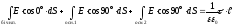

Оскільки і, то одержимо: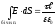

.

З міркувань симетрії випливає, що модуль Е є однаковим в усіх точках бічної поверхні. Тому винесемо Е за знак інтегралу:

. (3.46)

Інтеграл по бічній поверхні рівний площі цієї поверхні:

. (3.47)

Підставимо (3.47) у (3.46):

. (3.48)

З цієї формули випливає, що напруженість електричного поля, створеного нескінченою рівномірно зарядженою прямою обернено пропорційна до відстані між даною точкою простору і прямою. Ця формула справедлива також для нескінченого прямого рівномірно зарядженого циліндра.