2) Потік вектора напруженості та індукції електричного поля. Теорема Остроградського-Гауса

Нехай в просторі існує електричне поле, створене деякими електричними зарядами. Розглянемо деяку поверхню з нескінченно малою площею dS (елементарну поверхню) з одиничним вектором нормалі до поверхні , як зображено на рис.3.3. Нехай в центрі елементарної поверхні напруженість електричного поля рівна.

Елементарним потоком вектора напруженості електричного поля називається скалярна величина, рівна скалярному добуткові вектора напруженості електричного поля і одиничного вектора нормалі на площу елементарної поверхні:

Рис.3.3

де – кут між векторамиі.

Подібним чином можна дати визначення елементарного потоку вектора індукції електричного поля, який рівний:

Потік вектора напруженості електричного поля через деяку поверхню S визначається за формулою:

Він пропорційний числу силових ліній, які пронизують цю поверхню.

Потік вектора індукції електричного поля через деяку поверхню S рівний:

Розглянемо деякий точковий позитивний заряд , який помістимо в центрі сферичної поверхніS радіусом R (рис. 3.4). Обчислимо потік вектора напруженості електричного поля через цю замкнену поверхню

. (3.14)

Напруженість електричного поля точкового заряду в будь якій точці сферичної поверхні рівна

. (3.15)

Підставимо (3.15) в (3.14), врахуємо, що кут між векторами ів даному випадку.

.

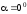Оскільки для всіх точок сферичної поверхні величина R є постійною то, винісши постійні множники за знак інтегралу, отримаємо:

. (3.16)

Але інтеграл по замкнутій поверхні S - це площа сферичної поверхні, яка рівна:

. (3.17)

Підставимо вираз (3.17) в (3.16):

. (3.18)

Український вчений М.В.Остроградський і німецький вчений К.Гаус довели, що формула (3.18) справедлива для замкненої поверхні довільної форми і довільної кількості електричних зарядів, які знаходяться всередині цієї поверхні. Тому в загальному випадку формулу (3.18) можна представити у вигляді:

. (3.19)

Формула (3.19) – це теорема Остроградського-Гауса для напруженості електричного поля: потік вектора напруженості електричного поля через довільну замкнену поверхню рівний алгебраїчній сумі електричних зарядів, охоплених цією поверхнею, поділеній на діелектричну проникність середовища.

Помножимо рівняння (3.19) на . Враховуючи, що цей множник постійний, внесемо його під знак інтегралу:

. (3.20)

Враховуючи (3.7), отримаємо

. (3.21)

Формула (3.21) це теорема Остроградського-Гауса для індукції електричного поля: потік вектора індукції електричного поля через довільну замкнену поверхню рівний алгебраїчній сумі електричних зарядів, охоплених цією поверхнею.

Розглянемо випадок коли електричні заряди розподілені в просторі неперервно з деякою об’ємною густиною .Об’ємною густиною електричного заряду називається фізична величина, рівна електричному зарядові в одиниці об’єму простору:

.

Визначимо з цієї формули dq:

Проінтегрувавши вираз (3.23) по деякому об’єму V визначимо сумарний електричний заряд який міститься в цьому об’ємі:

. (3.24)

З врахуванням формули (3.24) теорему Остроградського-Гауса (3.19) і (3.21) у випадку неперервного просторового розподілу зарядів можна представити у вигляді: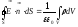

. (3.25)

. (3.26)

У формулах (3.25) і (3.26) інтегрування здійснюється по всьому об’єму V який обмежений замкненою поверхнею S.