5.Додавання подій

Сумою подій А і В називається подія С, яка полягає у здійсненні під час одиничного випробовування або події А, або події В, або обох разом.

Враховуючи означення суми двох подій і поняття несумісних подій, зауважимо, що сумою С двох несумісних подій А і В є подія, яка полягає в здійсненні або події А, або події В. Одночасна поява подій А і В виключена.

Теорема. Імовірність суми двох несумісних подій дорівнює сумі ймовірностей цих подій, тобто

Доведення. Нехай у результаті деякого випробування відбувається n елементарних подій. Зобразимо ці події n точками. Нехай з усіх n подій події А сприяють m подій, а події В - k подій. Тоді ймовірність події А є

а події В є

Оскільки події А і В несумісні, то немає подій, які б одночасно сприяли обом подіям А і В. Очевидно, що події А+В сприяють m+k подій, тому

Підставляючи значення Р(А), Р(В), Р(А+В) у рівність, дістанемо тотожність, що і доводить теорему.

Наслідок 1. Сума ймовірностей несумісних подій, що утворюють повну групу, дорівнює 1

Оскільки за умовою дані події несумісні, то до них можна застосувати теорему додавання

Дві події називаються протилежними, якщо одна і лише одна з них обов'язково здійсниться в даному випадку.

Якщо А - деяка подія, то протилежна їй подія позначається . ПодіїА і утворюють повну групу несумісних подій.

Наслідок 2. Сума ймовірностей протилежних подій дорівнює 1.

6.Множення подій. Залежні і незалежні події.

Формули множення ймовірностей для залежних та незалежних випадкових подій.

Нехай подія А є добутком двох подій В і С. Тоді:

а) якщо події В і С незалежні, то P(A)=P(BC)=P(B)*P(C);

б) якщо події В і С залежні, то P(A)=P(BC)=P(B)*P(C/B).

Добутком двох подій А і В називається подія С, що полягає у здійсненні під час одиничного випробовування й події А, і події В.

Подія А називається від події В, якщо ймовірність події А не залежить від того, відбулась чи ні подія В.

Дві події А та В називають залежними, якщо ймовірність настання однієї з них залежить від того, настала друга подія чи ні.

7.Знаходження ймовірності однієї з декількох незалежних подій

8.Формула повної ймовірності. Фориула Байєса.

Нехай подія А може відбутися тільки за умови настання однієї із несумісних подій (i = 1, 2,…, n), які утворюють повну групу. Тоді ймовірність події А подається формулою:

де — імовірність події— умовні ймовірності настання подіїА.

Наведена залежність називається формулою повної ймовірності.

Подія А може відбутись одночасно з деякою із подій Відомі ймовірності подій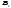та умовні ймовірності того, що подіяА відбудеться. Відомо, що в результаті випробування подія А відбулась. Потрібно з огляду на це переоцінити ймовірності гіпотез Для цього застосовують формулу Баєса:

9.Формула Бернуллі Імовірність того, що в n незалежних випробуваннях, у кожному з яких імовірність Р(А) = р, подія А відбудеться m раз, подається так:

Формула застосовується, якщо

Імовірність того, що в результаті n незалежних експериментів подія А з’явиться від mi до mj раз, обчислюється так:

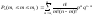
10.Знаходження ймов. Числа події в n-незалежних дослідах 11.Локальна і інтегральнаЛокальна теорема Лапласа. Імовірність того, що в n незалежних випробуваннях, у кожному з яких Р(А) = р, подія А відбудеться m раз, подається такою наближеною залежністю:

Локальна теорема Лапласа дає змогу обчислювати ймовірності , якщоn > 10 i p > 0,1.

Інтегральна теорема Лапласа. Імовірність того, що подія А відбудеться від дораз при проведенніn незалежних випробувань, у кожному з яких подія А відбувається з імовірністю р, подається формулою:

—функція Лапласа;

Значення функції Лапласа наводяться у спеціальних таблицях.