1.Формули комбінаторики

Основний принцип комбінаторики (правило множення). Нехай треба поcлідовно виконати k дій. Якщо першу можна виконати n₁ способами, після чого другу — n₂ способами, третю — n₃ способами і т. д., то всі k дій може бути виконано 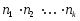способами.

Комбінації (сполуки) з n елементів по k. Нехай A — множина з n елементів. Довільна k-елементна підмножина множин з n елементів називається комбінацією з n елементів по k. Порядок елементів у підмножинах неістотний. Число k-елементних підмножин множини з n елементів позначають 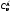. Воно дорівнює:

де

Домовимось, що 0!=1, тоді

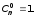
Справедливі властивості:

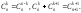
Перестановки. Множина з n елементів називається впорядкованою, якщо кожному елементу цієї множини поставлено у відповідність певне число (номер елемента) від 1 до n так, що різним елементам відповідають різні числа. Упорядковані множини вважаються різними, якщо вони відрізняються або своїми елементами, або порядком їх.

Різні впорядковані множини, які відрізняються тільки порядком елементів (тобто можуть бути утворені з тієї самої множини), називаються перестановками цієї множини. Число перестановок множини з n елементів дорівнює :

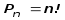
Розміщення з n елементів по k. Упорядковані k-елементні підмножини мно­жини, що містить n елементів, називаються розміщенням з n елементів по k. Число розміщень з n елементів по k дорівнює:

Біном Ньютона. 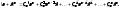де — натуральне число. Якщото

Величина

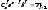
є (k+1)-й член в розкладенні бінома,

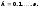
Число способів розбиття множини з n елементів на m груп. Нехай k₁, k₂, …, k_m — цілі невід'ємні числа, причому k₁ + k₂ + …+ k_m = n. Число способів, якими можна подати множину A з n еле­ментів у вигляді суми n множин, що містять відповідно k₁, k₂, …, k_m елементів, дорівнює:

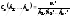
Перестановки з повтореннями. Число різних перестановок, які можна утворити з n елементів, серед яких є k₁ елементів першого типу, k₂ елементів другого типу, ...,k_m елементів m-го типу, дорівнює:

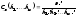
2.Формула Бінома-Ньютона

Рівність (a+b)n=C0n an b0+C1n an−1 b1+C2n an−2 b2 + ... + Cnn a0 bn називають біномом Ньютона.

3.Ймовірність події. Класичне означення.

Простір  елементарних подій називається дискретним, якщо множина  скінченна або зліченна.

Нехай простір елементарних подій  = {w₁, w₂, …, w_n, …} дискретний. Припустимо, що кожній елементарній події w_k можна поставити у відповідність невід'ємне число р_k (ймовірність w_k), причому 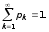ЯкщоA — випадкова подія (A  ), то

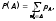де P(A) називається ймовірністю події A. Мають місце властивості:

а) P(A)≥0;

б) P(AB) = P(A) + P(B), якщо події A і B несумісні;

в) P()=1.

Нехай простір  складається з n елементарних рівноможливих подій (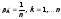), а до складуA входять m з цих подій. Тоді

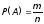—класичне означення ймовірності.

4.Статистичне означення ймовірності. Геометричної ймовірності.

Статистичною ймовірністю події А називається відношення кількості m випробувань, в яких подія А відбулась, до загальної кількості виконаних випробувань n: W(A)= m /n.

Суть геометричної ймовірності така. Нехай в деякій обмеженій множині  n-вимірного евклідового простору, що має міру Лебега mes(), навмання вибирають точку. Під висловом “точка, взята навмання” або “точка, навмання кинута у деяку множину”, розуміється, що ймовірність P(A) того, що точку буде взято з множини A  , дорівнює: