1. Непараметричні методи оцінювання законів розподілу випадкової величини

1.1. Побудова інтервального варіаційного ряду

Непараметричний метод оцінювання закону розподілу випадкової величини полягає в оцінюванні форми розподілів по вибірці реалізації випадкової величинибез припущення, що закон розподілує відомою функцією з точністю до параметрів. У результаті такого оцінювання одержують статистичний аналог закону розподілу випадкової величини.

Якщо об’єм вибірки достатньо великий (), то для побудови статистичного аналогу закону розподілу випадкової величинивикористовується інтервальний варіаційний ряд, у якому значення реалізацій випадкової величинигрупуютьсяза інтервалами.

При виборі рівних інтервалів ширина інтервалів визначається за формулою:

,

де – розмах варіаційного ряду;– максимальне значення реалізації випадкової величини у вибірці;– мінімальне значення реалізації випадкової величини у вибірці;n – об’єм вибірки; k – число інтервалів (ціла частина знаменника, округленого у більшу сторону).

При обсязі вибірки число інтервалів повинно знаходитися в межах. Тоді ширина інтервалуможе бути визначена за формулою:

.

Для побудови інтервалів за нижню межу першого інтервалу приймається величина

.

Нижня межа другого інтервалу збігається з верхньою межею першого і дорівнює:

.

Цей процес продовжується до k-го інтервалу, до того ж за верхню межу останнього інтервалу приймаємо величину

.

Визначивши шкалу інтервалів, роблять розподіл елементів вибірки (варіант) за інтервалами, перебираючи їх у порядку запису по вибірці.

Якщо значення варіанти співпало з межею інтервалу, то це значення відносять до інтервалу, що лежить зліва від границі, з якою він збігається (крім значення варіанта , що варто віднести до першого інтервалу).

Розподіливши елементи вибірки за інтервалами, для кожного інтервалу визначають такі величини:

1) частоту попадання елементів вибірки в-й інтервал;

2) відносну частоту попадання елементів вибірки в-й інтервал:

;

3) представник -го інтервалу:

.

У результаті одержуємо інтервальний варіаційний ряд, поданий у табл.1.1

Таблиця 1.1 – Інтервальний варіаційний ряд

Номер -го інтервалу	1	2	...	i	...	k
Межа -го інтервалу			...		...
Частота попадання в -й інтервал			...		...
Відносна частота попадання в -й інтервал			...		...
Представник -го інтервалу			...		...
Щільність відносної частоти			...		...

1.2. Побудова гістограми частот

Для побудови статистичного аналогу щільності розподілу випадкової величинитабл.1.1 доповнюється рядком, у якому розташовується щільність відносної частоти, яка визначається так:

.

Для графічного зображення варіаційного ряду служить гістограма – ряд зімкнутих прямокутників, основою кожного з яких є ширина інтервалу , а висота дорівнює або частоті, або частості, або щільності відносної частоти.В останньому випадку гістограма є аналогом щільності розподілу випадкової величини. На рис.1.1 подано всі три типи гістограм.

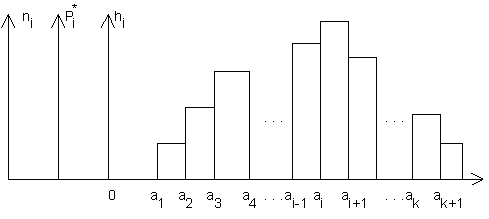
Рисунок 1.1 – Гістограми