
Лабы_идентификация
.pdfМІНІСТЕРСТВО ОСВІТИ І НАУКИ, МОЛОДІ ТА СПОРТУ УКРАЇНИ НАЦІОНАЛЬНІЙ УНІВЕРСИТЕТ
ХАРЧОВИХ ТЕХНОЛОГІЙ
ІДЕНТИФІКАЦІЯ ТА МОДЕЛЮВАННЯ ОБ’ЄКТІВ АВТОМАТИЗАЦІЇ
МЕТОДИЧНІ ВКАЗІВКИ до виконання лабораторних робіт
для студентів за напрямом підготовки 6.050202 “Автоматизація та комп’ютерно-інтегровані технології”
денної та заочної форм навчання
Київ НУХТ 2011
Ідентифікація |
та |
моделювання |
об’єктів автоматизації. Методичні |
|
вказівки |
до виконання |
лабораторних |
робіт для студентів за напрямо |
|
підготовки |
6.050202 |
“Автоматизація та комп’ютерно-інтегровані технології” |
||
денної та заочної форм навчання/ Уклад.: В.Д. Кишенько, С.А. Киричук, Є.С. Проскурка. – К.: НУХТ, 2011. – 19 с.
Рецензент: Б.М. Гончаренко, д-р. техн. наук, професор
Укладачі: В.Д. Кишенько, канд. техн. наук
С.А. Киричук Є.С. Проскурка
Відповідальний за випуск А.П. Ладанюк, д-р. техн. наук, проф.
Видання подається в авторській формі
2
Лабораторна робота №1 Побудова математичних моделей статичних, стохастичних об’єктів
управління методом найменших квадратів
Мета роботи: Освоїти методику проведення пасивного експерименту та обробки експериментальних даних за методом найменших квадратів.
|
Загальні відомості |
|
|
|
|
Статичною |
характеристикою (математичною |
моделлю |
статики) |
||
об’єкта управління називається функціональна |
залежність вихідних |
величин |
|||
об’єкта від вхідних діянь (збурення / управління) |
в усталеному режимі роботи |
||||
об’єкта, коли всі його змінні є сталими в часі. |
|
|
|
|
|
Стохастичним об’єктом називається об’єкт, |
в |
якому всі його |
змінні |
||
змінюються як випадкові процеси. Ці випадкові процеси підкоряються певним |
|||||
статистичним закономірностям. |
|
|
|
|
|
Більшість технологічних об’єктів управління є стохастичними об’єктами, |
|||||
в яких змінні є випадковими процесами з нормальним(Гаусовим) законом |
|||||
розподілу. У цьому випадку може бути виявлена в процесі експериментута |
|||||
обробки експериментальних даних статистична |
закономірність– рівняння |
||||
регресії, яка відтворює статистичну залежність математичного сподівання вихідної величини від вхідних дій.
Такі |
|
моделі (закономірності) |
отримуємо |
в |
результаті |
обробки |
|||||||
експериментальних даних пасивного чи активного експерименту. |
|
|
|
|
|||||||||
Експериментом |
|
називають |
взаємодію |
дослідника |
з |
об’єк |
|||||||
дослідження, |
в |
результаті |
якої |
шляхом |
вимірювання |
отримують |
дан |
||||||
спостереження в кількісній чи якісній формі – експериментальні дані. |
|
|
|||||||||||
Пасивний експеримент |
полягає |
у спостережені |
за |
функціонуванням |
|||||||||
об’єкта, шляхом вимірювання всіх його змінних, що входять в модель без |
|
||||||||||||
нанесення на об’єкт спланованих діянь. |
|
|
|
|
|
|
|
||||||
Одним з методів побудови математичних |
моделей таких |
стохастичних |
|
||||||||||
об’єктів |
є метод |
найменших |
квадратів. Метод |
найменших |
квадратів– |
це |
|
||||||
метод параметричної ідентифікації об’єктів управління. |
|
|
|
|
|
||||||||
Ідентифікація – |
це |
процес побудови |
математичної моделі об’єкта |
||||||||||
управління за експериментальними даними та деякою апріорною(до дослідів) |
|
||||||||||||
інформацією |
(дані |
про |
особливості |
об’єкта: детермінований-стохастичний, |
|
||||||||
лінійний-нелінійний, неперервний-дискретний, стаціонарний-нестаціонарний; |
|
||||||||||||
інформація про алгоритм та критерії ідентифікації), при цьому математична |
|
||||||||||||
модель повинна бути оптимальною, забезпечуючи екстремальне значення |
|
||||||||||||
критерію адекватності. |
|
|
|
|
|
|
|
|
|
|
|||
Адекватність – |
це |
міра відповідності |
моделі об’єкту. В більшості |
|
|||||||||
випадків |
оцінюється |
за |
допомогою |
показників-критеріїв |
адекватності, які |
|
|||||||
зв’язують вихідні змінні моделі та об’єкта.
Математичні моделі об’єктів управління складаються з двох основних компонентів:
3

- |
структури S; |
|
- |
параметрів цієї структури АS. |
|
|
M <S, AS > |
(1.1) |
Структура математичної моделіS являє |
собою сукупність елементів |
|
(вхідні та вихідні змінні), форм зв’язків між цими елементами, типів зв’язків. Тип зв’язку лінійний:
у = а0+а1х1+а2х2 де у, х1, х2 – елементи; а0, а1, а2 – параметри;
Тип зв’язку лінійний, степеневий:
у = а0+а1х1+а2х12 де у, х1– елементи; а0, а1, а2 – параметри;
Тип зв’язку показниковий.
(1.2)
(1.3)
|
|
|
у = а0х1а1 |
|
|
(1.4) |
|
|
де у, х1– елементи; а0, а1 – параметри; |
|
|
|
|
|
|||
Параметрами структури є коефіцієнти рівняння, константи, за допомогою |
|
|||||||
яких кількісно оцінюється взаємозв'язок між змінними. |
|
|
|
|||||
При |
параметричній |
ідентифікації |
структура |
математичної |
моделі |
|||
визначається неформальним шляхом, частіше всього апріорі(до дослідів), на |
|
|||||||
основі досвіду застосування на об’єктах подібного класу, або шляхом |
|
|||||||
висунення |
декількох |
структур-претендентів, остаточний |
вибір |
найбільш |
||||
ефективної з них здійснюється в процесі обробки даних. |
|
|
|
|||||
Метод найменших квадратів є оптимізаційною задачею, критерієм |
|
|||||||
оптимальності якої є вираз: |
п |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ф= å ( у іе - у ім ) 2 ¾¾® min |
|
(1.5) |
|
|||
де і – номер експерименту; |
і =1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
n – загальна кількість експериментів; |
|
|
|
|
||||
уеі, умі – |
відповідно, |
значення |
вихідної |
величини |
об’єкта, отримані в |
|
||
результаті і-того експерименту |
та розраховані за математичною моделлю при |
|
||||||
значеннях вхідних дій, отриманих на і-тому експерименті. |
|
|
|
|||||
У випадку відомої структури рівняння (1.5) набуває вигляду: |
|
|
||||||
|
|
п |
|
r r |
|
|
(1.6) |
|
|
Ф= å ( у іе - f j |
( A j ; X ie )) 2 |
¾¾® min |
|
|
|||
і=1
Впостановці (1.6) метод найменших квадратів є задачею нелінійного
програмування.
У випадку, якщо функція fj є диференційованою, тоді задачу (1.6) можна вирішити градієнтними методами чи методами класичного аналізу. Якщо функція fj буде лінійною за одним параметром, то:
п |
|
|
|
||
Ф= å ( у іе - ( а 0 - а1 х )) 2 ¾¾® min |
(1.7) |
||||
і =1 |
|
|
|
||
Для вирішення задачі (1.7) знаходимо часткові похідні та прирівнюємо їх |
|||||
до нуля: |
|
|
|
||
|
дФ |
= 0; |
дФ |
= 0; |
(1.8) |
|
|
|
|||
|
да0 |
да1 |
|
||
4

Отримуємо систему лінійних алгебраїчних рівнянь, розв'язком якої є:
|
|
n |
n |
n |
n |
|
|
n |
n |
n |
|
а |
|
å yi åxi2 - åxi yi åxi |
; а |
|
nå yi xi - åxi å yi |
(1.9) |
|||||
= |
i=1 |
i=1 |
i=1 |
i=1 |
= |
i =1 |
i=1 |
i=1 |
|||
|
n |
n |
|
n |
n |
|
|||||
0 |
|
|
|
1 |
|
|
|
||||
|
|
|
nåxi2 - (åxi )2 |
|
|
nåxi2 - (åxi )2 |
|
||||
|
|
|
i=1 |
i=1 |
|
|
|
i=1 |
i=1 |
|
|
Опис лабораторної установки
Лабораторна установка складається із двох стендів рис. 1.1. На правому стенді розміщені вольтметр 1, регулюючий мікропроцесорні контролери Р-130 2, ПРОТАР 3, мнемосхема 4, електронний імітатор об’єкта 5. На лівому стенді знаходяться потенціометр -КСП4 6, вольтметр 7, амперметр 8, автотрансформатор 9. Нижче розміщена панель тумблерів керування 10.
Рис. 1.1. Схема лабораторної установки.
Порядок виконання роботи
1.Ввімкнути тумблер “возмущение” і вимкнути тумблер “сброс”. Потенціометром “возмущение” змінити напругу, яка контролюється вольтметром 1, у випадковій послідовності в межах від 2,5 до 5 В (вхідна змінна Х, В).
2.Слідкувати на потенціометрі 6 за змінюванням вихідної змінної Y (температура на виході об’єкта) до закінчення перехідного процесу.
3.Ввімкнути тумблер “сброс” і перейти до пункту 1.
5
4.Записати отримані експериментальні дані в таблицю1.1, сформувавши малу
та
велику вибірки (розмірність вибірки задається викладачем).
5.Побудувати кореляційні поля для експериментальних даних малої та великої вибірок.
6.Розрахувати параметри математичної моделі у = а0+а1х1 за формулами 1.9; визначити значення критерію Ф.
7.Розрахувати параметри математичних моделей у = а0+а1х1 та у = а0+а1х1+а2х12
звикористанням програм MNK11.bas та MNK22.bas для малої та великої вибірки; визначити значення критерію Ф для кожної моделі.
8.Проаналізувати за критерієм Ф отримані математичні моделі; зробити висновок
про адекватність отриманих моделей в залежності від величини вибірки експериментальних даних та структури моделей.
Таблиця 1.1
№екс |
|
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
6 |
|
7 |
|
8 |
|
9 |
|
10 |
|
11 |
|
12 |
|
13 |
|
14 |
|
|
Xei,В |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Yei, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
°С |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Yмi,л |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Yei,нл |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Yi,не |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
30 |
31 |
32 |
33 |
34 |
35 |
36 |
37 |
38 |
39 |
40 |
41 |
42 |
43 |
44 |
45 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Контрольні запитання
1.Що таке експеримент і чому він полягає?
2.Дайте визначення поняттю ідентифікації об’єктів управління.
3.Що передбачає методика проведення пасивного експерименту?
4.Поясніть алгоритм методу найменших квадратів.
5.Поясніть поняття про структуру та параметри математичної моделі
6
Лабораторна робота №2 Побудова математичної моделі статичного об'єкта управління методом
повного факторного експерименту Мета: освоїти методику активного експерименту та статистичного аналізу
результатів експерименту.
Загальні відомості
Активний експеримент передбачає нанесення на об'єкт спланованих діянь та у вимірюванні змінних, що входять в математичну модель.
Активні експерименти поділяють на 2 класи:
-“класичний”;
-методи планування експерименту.
Класичний метод полягає в тому, що інтервал змінювання вхідних дій (факторів) неформалізованим чином розбивається на декілька підінтервалів, кількість яких визначається дослідником, виходячи з міркувань точності
відтворення |
властивостей |
об, ’єктабільш |
детального |
дослідження |
окремих ділянок області функціонування об'єкта тощо. |
|
|||
Експеримент проводять, встановивши стабільне значення вхідних дій на деякому рівні. Ці значення повинні знаходитися у вибраному інтервалі.
Експеримент |
виконують на |
всіх визначених рівнях |
факторів з декількома |
||
повторами, з метою усунення систематичної похибки. Такий експеримент |
|||||
характеризується значною |
кількістю |
дослідів, але |
дає |
змогу для деяких |
|
об'єктів встановити властиві для цього об’єкта закономірності. |
|||||
Методи планування експерименту дозволяють різко скоротити кількість |
|||||
експериментів за рахунок того, що рівні факторів в кожному експерименті |
|||||
теоретично |
обґрунтовані |
і математична модель має однакові показники |
|||
ефективності (точність, адекватність) |
в порівняні з |
моделями, отриманими |
|||
класичним методом. Остання теза справедлива у випадку, |
якщо математична |
||||
модель за своєю структурою є типовою: лінійна, показникова, експоненціальна тощо, тобто тоді коли вона є диференційованою та гладкою.
Експеримент виконують згідно з планом експерименту, що являє собою матрицю планування експерименту. Ці матриці експерименту є універсальними, тому що координати рівнів факторів наведені у відносних одиницях по відношенню до центру плану експерименту.
Вбудь-якому експерименті використовуються крайні значення факторів,
атакож так звані “зоряні точки”, координати яких визначаються за спеціальними формулами в залежності від типу математичної моделі.
Вихідна змінна в методах плануванняексперименту називається функцією відгуку.
7
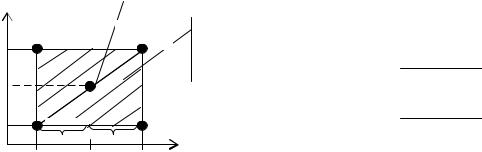
|
|
|
Центр плану експерименту |
|
|
|
|
X2 |
(-1;+1) |
|
(+1;+1) |
Область |
DХ і = Х імах - Х іном |
||
X2max |
|
|
|
існування |
Х імах - Х іном |
= +1 |
|
X1ном |
|
|
|
моделі. |
Х імах |
- Х іном |
|
|
|
|
|
|
|||
X2min |
(-1;-1) |
|
(+1;-1) |
|
Х іміп - Х іном |
= -1 |
|
|
|
|
|
мах |
ном |
||
|
X |
|
X |
|
Х і |
- Х і |
|
|
|
|
|
|
|
||
|
Х1min |
X1ном |
Х1max |
Х1 |
|
|
|
Рис. 2.1. Ілюстрація плану повного факторного експерименту.
Кількість експериментів при повному факторномуексперименті визначається типом математичної моделі і повинна забезпечити комбінацію всіх можливих рівнів фактору. Наприклад, при лінійній моделі кількість експериментів в одній повторності N=2n, де n – кількість факторів.
|
Для |
того, |
|
щоб розрахувати точність моделі потрібно провести |
|||||||
статистичний аналіз отриманих результатів. Як правило, експерименти |
|||||||||||
проводять з кількістю повторів не менше двох. |
|
Таблиця 2.1 |
|||||||||
|
|
|
|
|
|
|
|
|
|||
|
|
|
План |
|
Вихідні змінні |
Розрахунок |
|
||||
|
№ |
експерименту |
|
|
|||||||
|
|
|
|
|
|
|
|
||||
|
п/п |
Х1 |
|
Х2 |
Yu1 |
|
Yu2 |
Yu3 |
Ÿu |
Ŷu |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
+1 |
|
+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
-1 |
|
+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
+1 |
|
-1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
-1 |
|
-1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Опис лабораторної установки
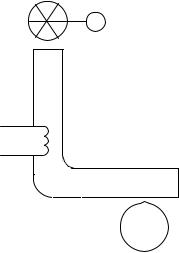
Дослідження проводяться на тепловому об'єкті (рис. 2.2), що являє собою коліноподібну трубу, в якій знаходиться електричний нагрівач в яку вентилятором подається холодне повітря. Вихідною змінною (функцією відгуку) Y є температура на виході з труби.
8
|
|
|
|
|
X2(φ) |
|
|
|
Першим фактором є напруга, що |
|||||||
|
|
|
|
|
|
|
|
подається на нагрівальний елемент Х1 (u), |
||||||||
|
|
|
|
|
|
|
|
другим фактором є швидкість обертання |
||||||||
|
|
|
|
|
|
|
|
вентилятора Х2(φ). |
отримати |
|
лінійн |
|||||
|
|
|
|
|
|
|
|
|
|
Потрібно |
|
|||||
|
X1(u) |
|
|
|
|
|
|
математичну модель такого вигляду: |
|
|||||||
|
|
|
|
|
|
|
|
|
|
Y=a0+a1X1+a2X2 |
фактор |
|||||
|
|
|
|
|
|
|
|
|
|
Враховуючи |
те, що |
перший |
||||
|
|
|
|
|
|
|
|
(напруга) |
змінюється |
|
за |
допомогою |
||||
|
|
|
|
|
ТЕ |
У(t) |
пневматичного |
виконавчого |
механізму, |
|||||||
|
|
|
|
|
положення якого визначається тиском |
|
||||||||||
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
стисненого повітря, визначаємо значення |
|
|||||||
Рис. 2.2. Структурна схема |
|
рівнів факторів в % ходу виконавчого |
|
|||||||||||||
|
|
теплового об’єкта. |
|
механізму, яким відповідають певні |
|
|||||||||||
значення тиску повітря, що подається на виконавчий механізм. |
|
|
|
|
||||||||||||
Х1= 50 % Х.ВМ |
|
|
|
|
0 % |
|
100 % |
|
|
|
||||||
Х1 =20% Х. ВМ. |
|
|
|
1 |
|
1 |
|
|
|
|
||||||
(+1) Х1мах =90% ~ 0,76 кгс/см2 |
|
0,2 кгс/см2 |
1,0 кгс/см2 |
|
|
|||||||||||
(-1) Х1мах =30% ~ 0,44 кгс/см2 |
|
|
|
|
|
|
|
|
|
|||||||
|
Швидкість вентилятора змінюється змінюванням положення |
|
|
|||||||||||||
потенціометра |
|
|
|
|
|
|
|
|
|
|
|
|
||||
Х2 |
ном – |
друга поділка, |
|
|
|
|
|
|
|
|
|
|
||||
Х2мах – перша поділка, |
|
|
|
|
|
|
|
|
|
|
||||||
Х2мін – третя поділка. |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Лабораторна установка (рис. 2.3) складається із теплового об’єкта, що |
|||||||||||||||
являє собою трубу9 з розміщеними в середині нагрівними елементами10. |
||||||||||||||||
Повітря в трубу подається вентилятором8. Вихідною величиною об’єкта є |
||||||||||||||||
температура |
повітря |
на |
виході |
з |
труби, а |
факторами – зміна |
напруги, що |
|||||||||
подається |
на |
нагрівні |
елементи10 та зміна витрати повітря, пропорційна |
|||||||||||||
частоті обертів п вентилятора, яка змінюється за допомогою змінного резистора |
||||||||||||||||
3. Напруга живлення нагрівника змінюється автотрансформатором7, повзун |
||||||||||||||||
якого переміщується мембранним виконавчим механізмом11. Температура в |
||||||||||||||||
об’єкті вимірюється термометром опору 12 в комплекті з автоматичним мостом |
||||||||||||||||
КСМ-3 1, що має пневмовихід, тобто виконує роль ЕПП. Регулятор ПР 3.31 (ПІ- |
||||||||||||||||
регулятор) встановлений на задній стінці вториного приладу2 типу ПВ10.1Э; |
||||||||||||||||
справа |
розміщений |
мікропроцесорний |
регулятор 4. |
Стенд |
|
вмикається |
за |
|||||||||
допомогою |
|
вимикача 6, |
пов’язаного з сигнальною лампою5. Швидкість |
|||||||||||||
обертання вентилятора регулюється перемикачем 3. |
|
|
|
|
|
|||||||||||
9

Рис. 2.3. Схема лабораторного стенду.
Порядок виконання роботи
1. Згідно з планом експерименту встановити за допомогою задатчика2 значення
фактора Х1, а за допомогою резистора 3 значення фактора Х2.
2.Після закінчення перехідного процесу записати значення функції відгуку Y в таблицю 2.1.
3.Експерименти повторити в трьох повторах згідно із планом експерименту.
Обробка експериментальних даних і їх статистичний аналіз.
2.1. Оцінка відтворюваності експериментальних даних.
Відтворюваність експериментальних даних вказує на те, чи вибрані нами фактори в діапазоні їх змінювання є впливовими на функцію відгуку чи ні.
Розрахувати математичні сподівання функції відгуку у кожном експерименті
m
å yuk
y u |
= |
k =1 |
(2.1) |
|
m |
||||
|
|
|
10
