
ІНДИВІДУАЛЬНЕ ЗАВДАННЯ 1
.docІНДИВІДУАЛЬНЕ ЗАВДАННЯ 1
Змістовий модуль 1 «Геометричні побудови на площині»
Варіант 1
-
Даним радіусом
 провести коло, яке проходить через дану
точку
провести коло, яке проходить через дану
точку
 і дотикається до даного кола
і дотикається до даного кола
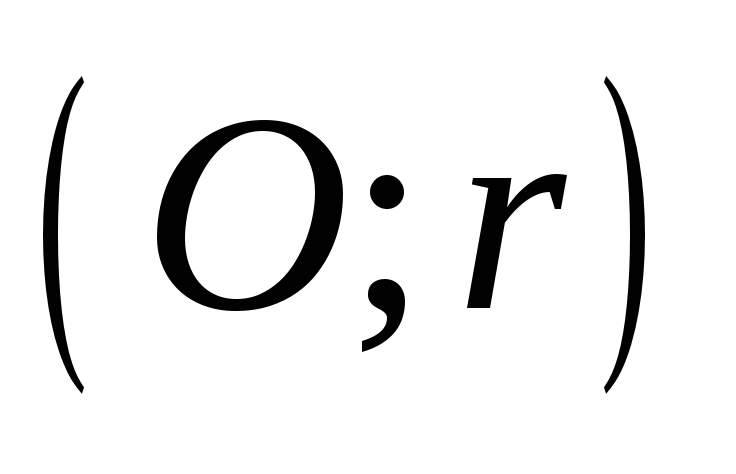 .
. -
Дано точку
 ,
пряму
,
пряму
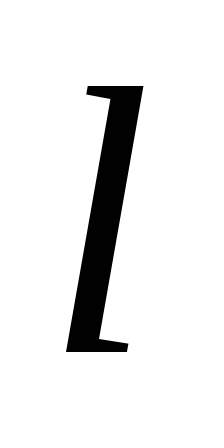 і коло
і коло
 .
Побудувати квадрат так, щоб діагоналі
його перетинались в точці
.
Побудувати квадрат так, щоб діагоналі
його перетинались в точці
 ,
одна вершина належала прямій
,
одна вершина належала прямій
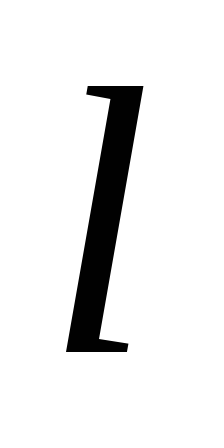 ,
а інша вершина – колу
,
а інша вершина – колу
 .
. -
Побудувати трикутник, знаючи відношення його сторін
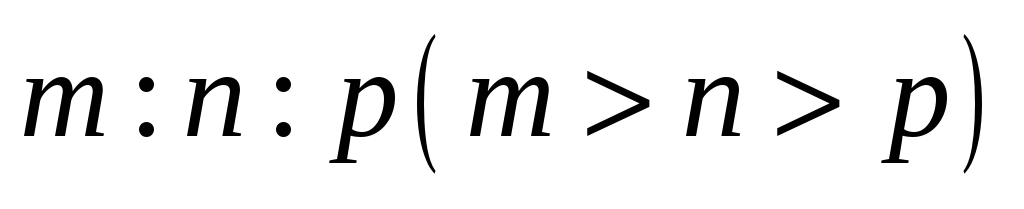 і бісектрису найбільшого з його кутів.
і бісектрису найбільшого з його кутів. -
Всередині кута АСВ знаходяться точки
 і
і
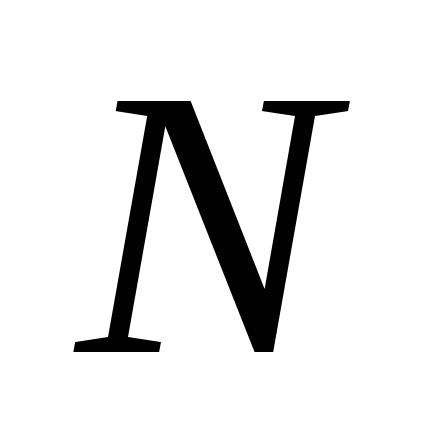 .
Знайти на сторонах кута точки
.
Знайти на сторонах кута точки
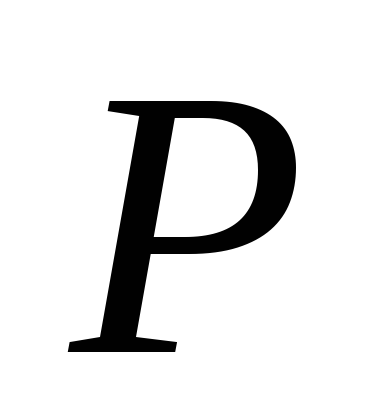 і
і
 такі, щоб ламана
такі, щоб ламана
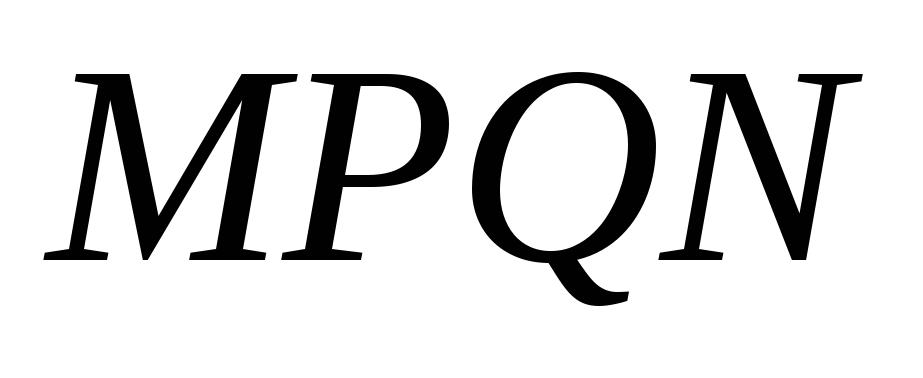 була мінімальною.
була мінімальною. -
Побудувати паралелограм за двома діагоналями і кутом між сторонами.
-
Через дану точку провести січну до даного кола так, щоб її зовнішня частина була втричі більша, ніж внутрішня.
-
Довести, що дві трапеції, сторони яких попарно рівні, також рівні.
Варіант 2
-
Побудувати трапецію за її діагоналями, кутом між ними та бічною стороною.
-
Побудувати прямокутний трикутник, якщо відомо його катет
 ,
середина гіпотенузи знаходиться в
даній точці
,
середина гіпотенузи знаходиться в
даній точці
 ,
а кінці гіпотенузи – один на даному
колі
,
а кінці гіпотенузи – один на даному
колі
 ,
другий – на даній прямій
,
другий – на даній прямій
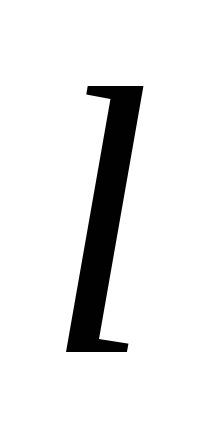 .
. -
Дано два концентричних кола. Побудувати квадрат так, щоб дві його суміжні вершини належали одному колу, а дві інші – другому.
-
У даний трикутник вписати другий трикутник так, щоб його сторони були відповідно паралельні сторонам даного трикутника.
-
Побудувати коло, яке дотикається до даної прямої в даній точці і до даного кола
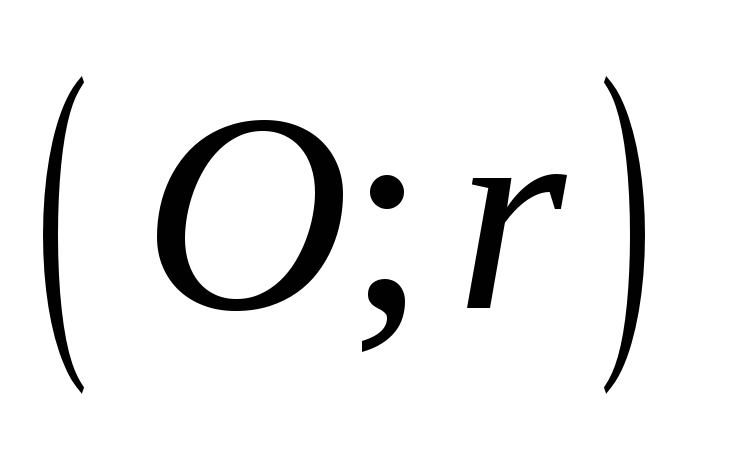 .
. -
Побудувати відрізок
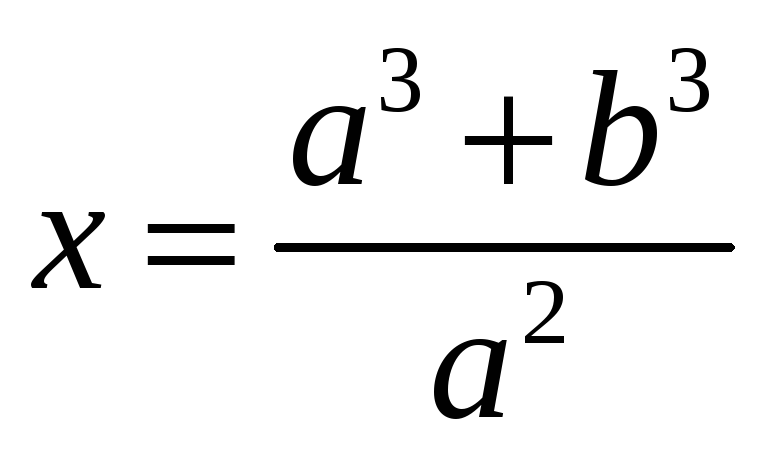 (
( і
і
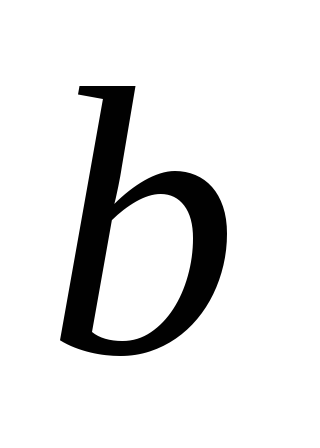 – дані відрізки).
– дані відрізки). -
На сторонах паралелограма поза ним побудовано квадрати. Довести, що їх центри утворюють квадрат.
Варіант 3
-
Між пунктами
 і
і
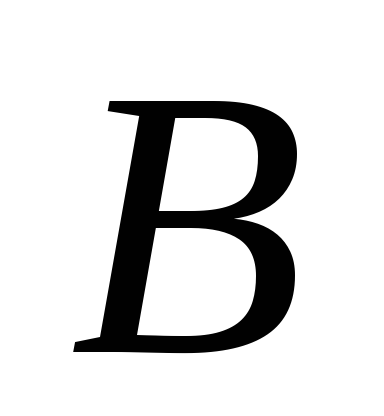 проходить канал з паралельними берегами.
Де треба вибрати місце для побудови
моста через канал, щоб шлях від
проходить канал з паралельними берегами.
Де треба вибрати місце для побудови
моста через канал, щоб шлях від
 до
до
 був найкоротший?
був найкоротший? -
Знайти геометричне місце точок, дотичні з яких до даного кола вдвічі менше січних, які проведені з цих же точок через центр кола.
-
Побудувати рівнобедрений прямокутний трикутник так, щоб вершина його прямого кута знаходилась в даній точці
 ,
друга – на даному колі
,
друга – на даному колі
 ,
а третя – на даній прямій
,
а третя – на даній прямій
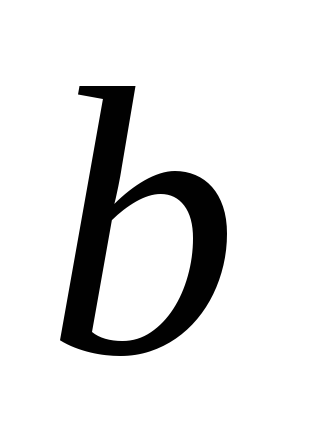 .
. -
Через точку перетину двох даних кіл провести пряму, на якій ці кола відсікають рівні хорди.
-
У даний трикутник вписати паралелограм з даним кутом
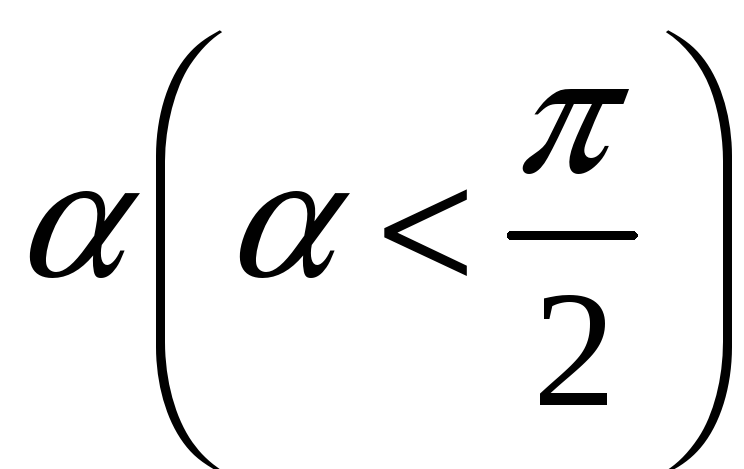 і відношенням двох сторін паралелограма
і відношенням двох сторін паралелограма
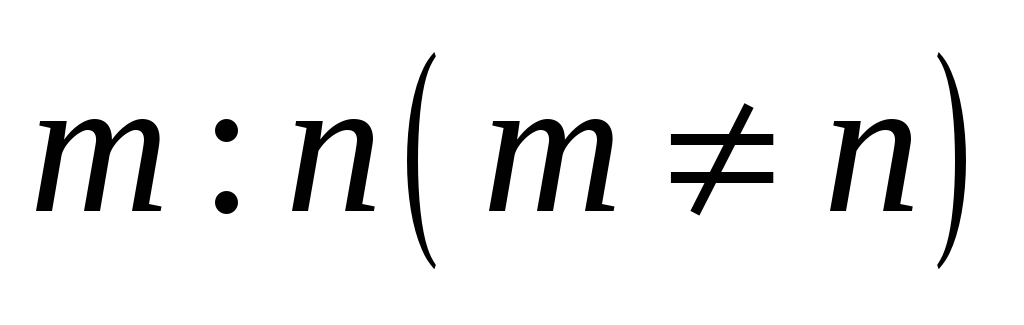 так, щоб дві вершини паралелограма
лежали на основі, а дві інші – на бічних
сторонах трикутника.
так, щоб дві вершини паралелограма
лежали на основі, а дві інші – на бічних
сторонах трикутника. -
У дане коло вписати прямокутник, рівновеликий даному квадрату.
-
Протилежні сторони шестикутника паралельні та рівні. Довести, що шестикутник має центр симетрії.
Варіант 4
-
Побудувати ромб, дві суміжні вершини якого знаходяться у двох даних точках, а точка перетину діагоналей – на даному колі.
-
Між сторонами даного кута розмістити відрізок, рівний даному, так, щоб він відтинав від сторін кута рівні відрізки.
-
Побудувати правильний трикутник, висоти якого перетинаються в даній точці, а дві вершини лежать на даному колі.
-
Побудувати квадрат, дві протилежні вершини якого лежать на даній прямій
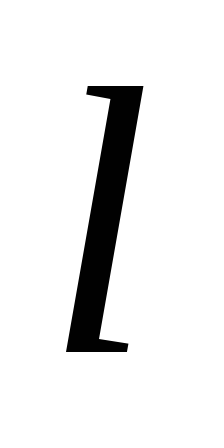 ,
третя – на даній прямій
,
третя – на даній прямій
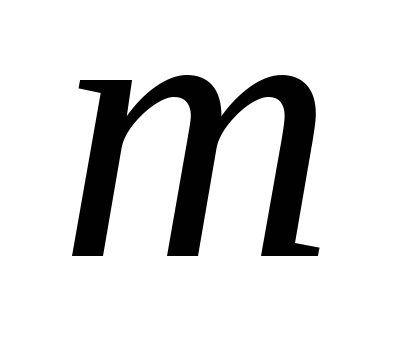 ,
а четверта – на даному колі
,
а четверта – на даному колі
 .
. -
У даний сектор вписати квадрат.
-
Побудувати множину точок таких, що проведені з них дотичні до даного кола вдвічі менші січних, проведених із цих же точок через центр даного кола.
-
Довести, що образи даної точки при симетрії відносно середин сторін чотирикутника є вершинами паралелограма.
Варіант 5
-
Побудувати трапецію за основою
 ,
діагоналями
,
діагоналями
 і
і
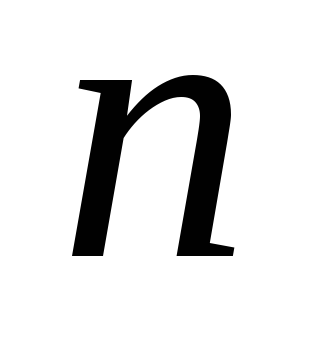 та кутом між діагоналями
та кутом між діагоналями
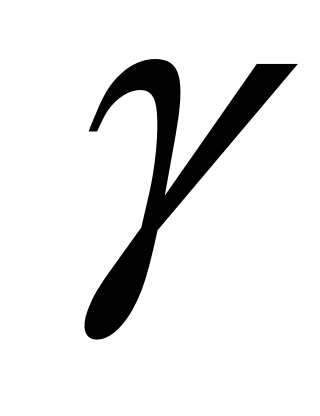 .
. -
Побудувати трикутник за основою і протилежним кутом, якщо відомо точку на основі, через яку проходить бісектриса кута при вершині.
-
Побудувати паралелограм, точка перетину діагоналей якого знаходиться в даній точці
 ,
якщо відомі чотири його точки (по одній
на кожній стороні).
,
якщо відомі чотири його точки (по одній
на кожній стороні). -
Побудувати чотирикутник за його діагоналями, кутом між ними і двома суміжними сторонами.
-
Дано два кола та пряма між ними. Побудувати правильний трикутник так, щоб дві його вершини належали даним колам, а одна висота лежала на даній прямій.
-
Побудувати відрізок
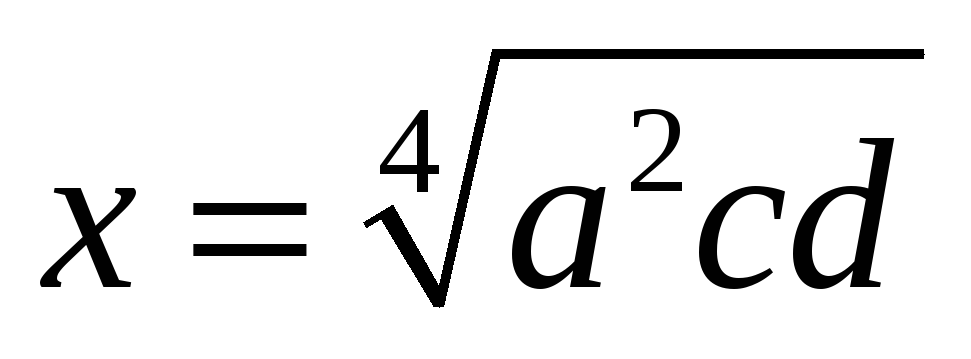 (
(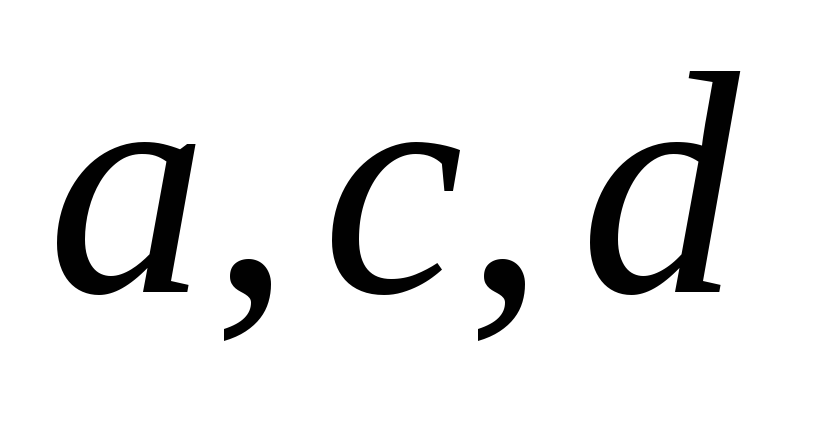 –
дані відрізки).
–
дані відрізки). -
У крузі з центром
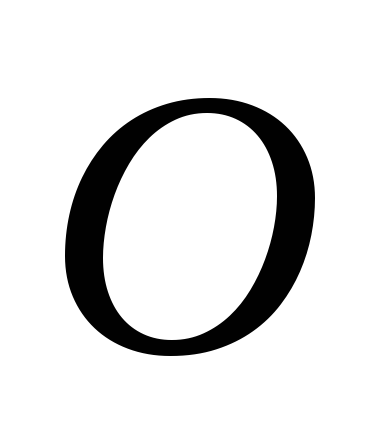 проведено хорду
проведено хорду
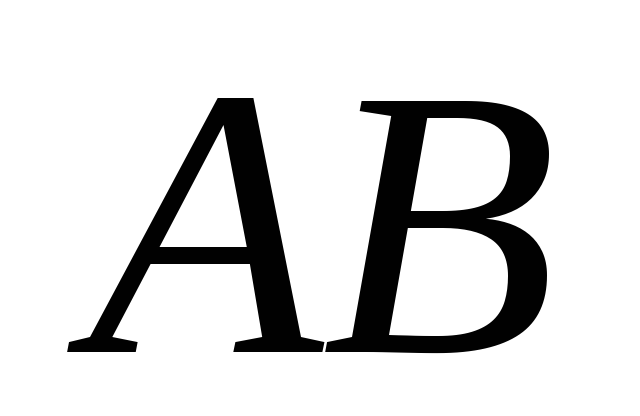 .
На радіусі
.
На радіусі
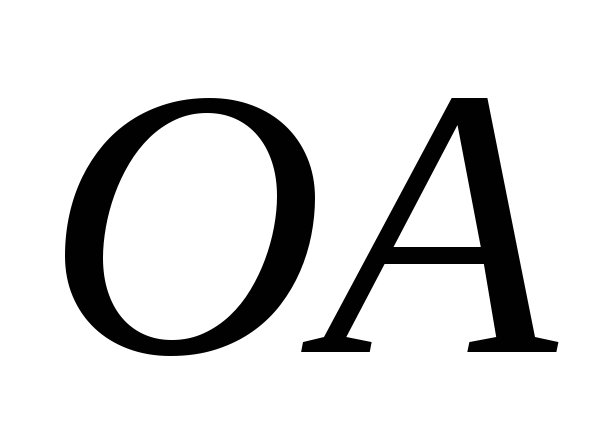 ,
як на діаметрі, побудовано коло
,
як на діаметрі, побудовано коло
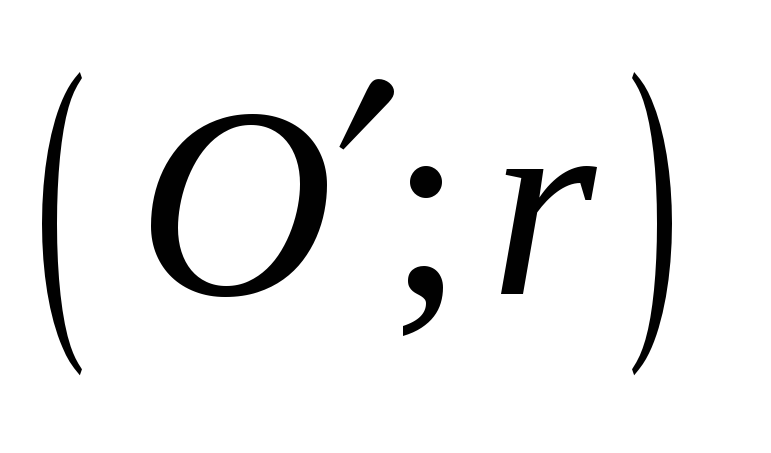 .
Довести, що площі двох сегментів, які
відсікаються хордою
.
Довести, що площі двох сегментів, які
відсікаються хордою
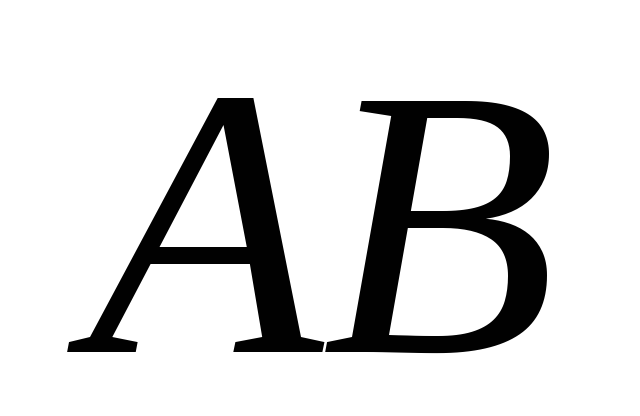 від обох кругів, відносяться як 4:1.
від обох кругів, відносяться як 4:1.
Варіант 6
-
Дано два концентричних кола і точка
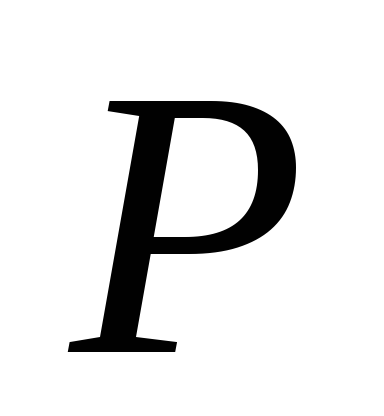 між ними. Через точку
між ними. Через точку
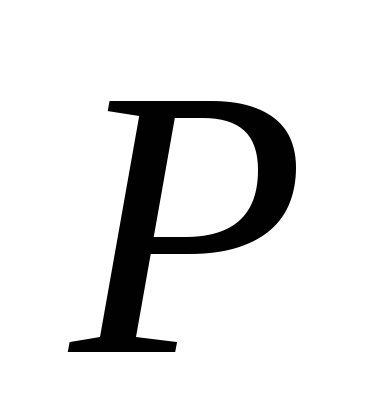 провести коло, дотичне до даних кіл.
провести коло, дотичне до даних кіл. -
Побудувати паралелограм, дві протилежні вершини якого знаходились би в даних точках, а дві – інші на даному колі.
-
Дано два кола
 і
і
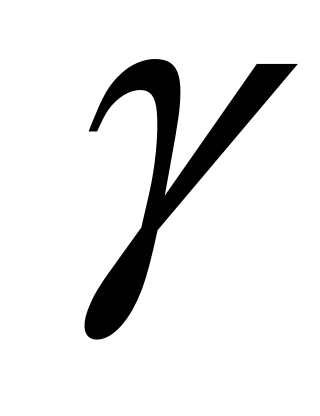 і точка
і точка
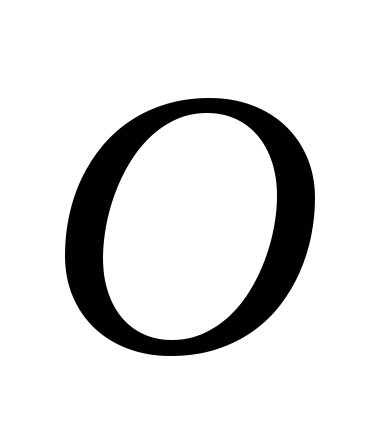 .
Побудувати квадрат, діагоналі якого
перетинались би в точці
.
Побудувати квадрат, діагоналі якого
перетинались би в точці
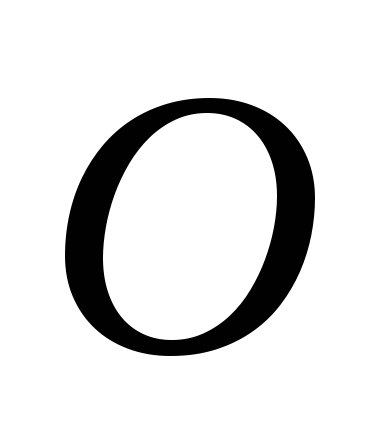 ,
а дві протилежні вершини знаходились:
одна – на колі
,
а дві протилежні вершини знаходились:
одна – на колі
 ,
друга – на колі
,
друга – на колі
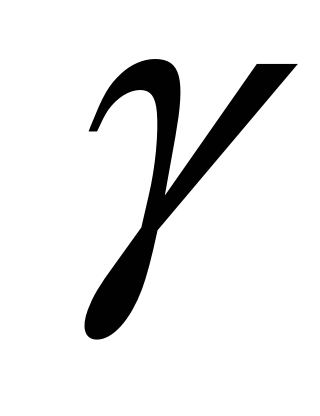 .
. -
У даний кут вписати коло, що проходить через дану точку.
-
Дано точки
 і
і
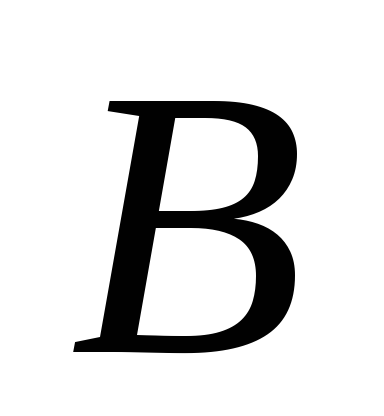 по один бік від прямої
по один бік від прямої
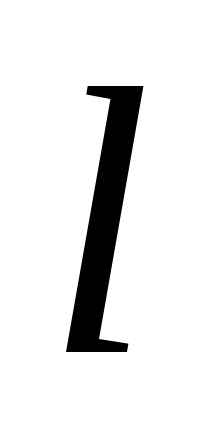 .
Розташувати на прямій
.
Розташувати на прямій
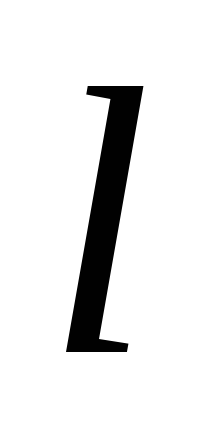 відрізок
відрізок
 довжиною
довжиною
 так, щоб ламана
так, щоб ламана
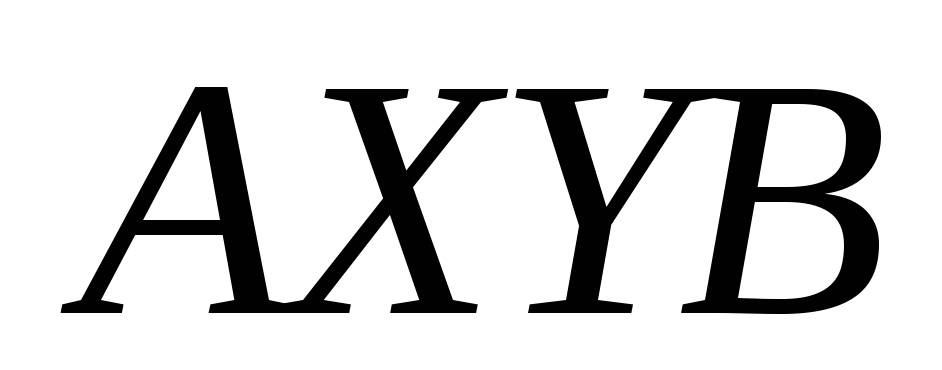 мала найменшу довжину.
мала найменшу довжину. -
Побудувати квадрат, площа якого вдвічі менша площі даного квадрата.
-
На катетах
 і
і
 рівнобедреного прямокутного
рівнобедреного прямокутного
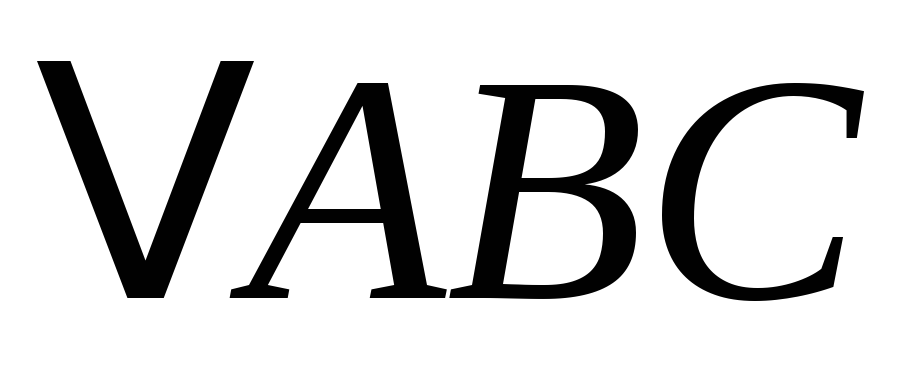 вибрано точки
вибрано точки
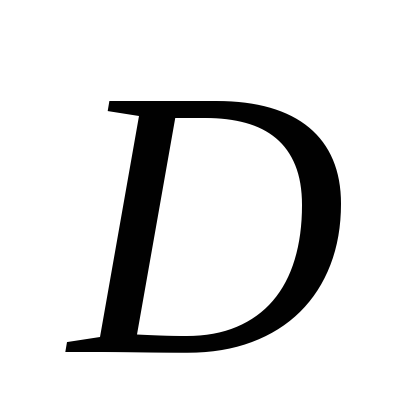 і
і
 так, що
так, що
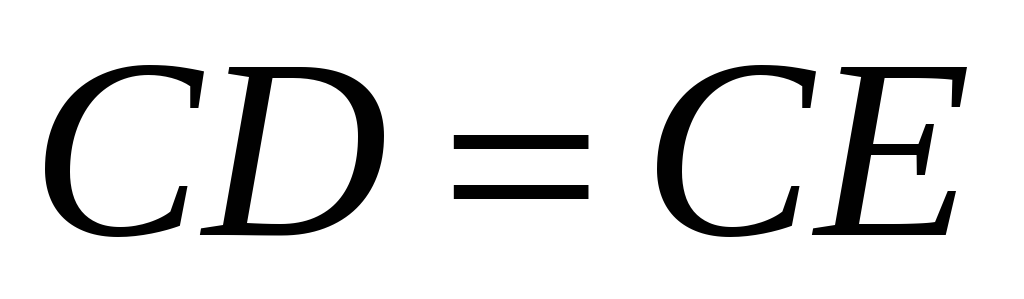 .
Прямі, що проведені через точки
.
Прямі, що проведені через точки
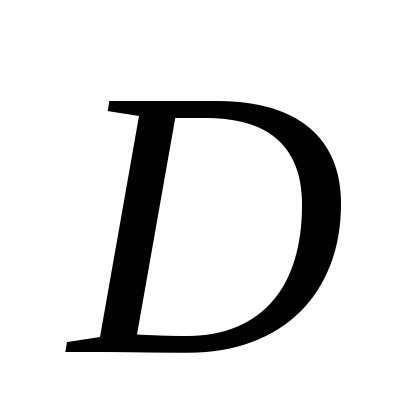 і
і
 перпендикулярно до
перпендикулярно до
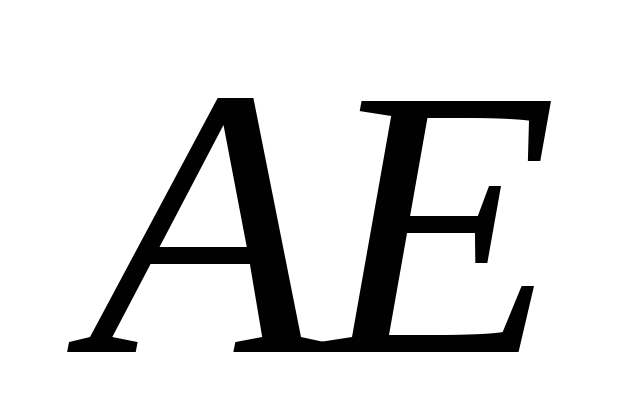 ,
перетинають гіпотенузу
,
перетинають гіпотенузу
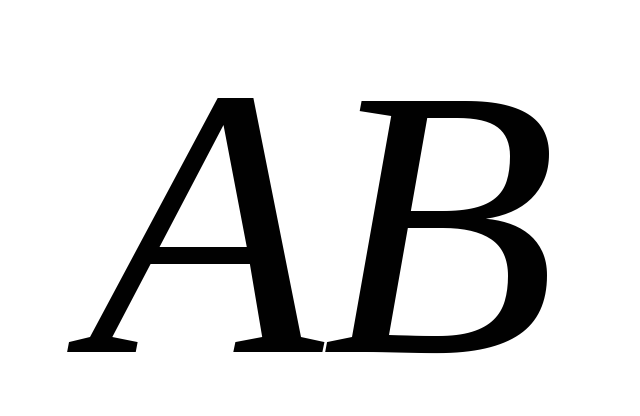 відповідно в точках
відповідно в точках
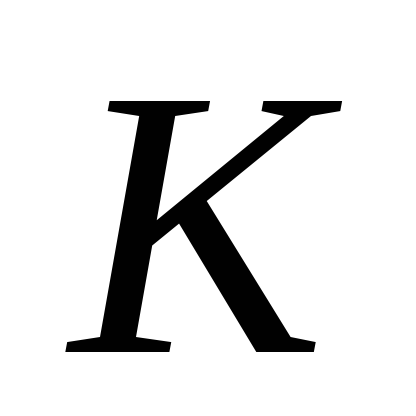 і
і
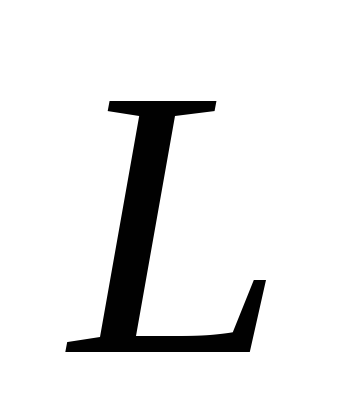 .
Довести, що
.
Довести, що
 .
.
Варіант 7
-
Побудувати чотирикутник АВСД , якщо дано його сторони і відомо, що діагональ АС ділить кут А навпіл.
-
Через дану точку
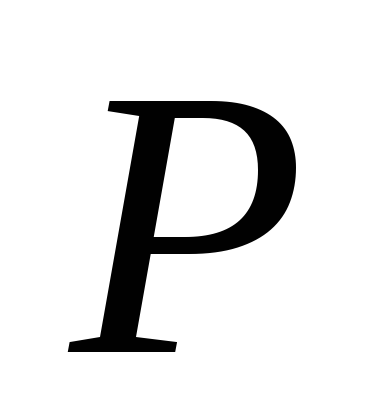 в крузі
в крузі
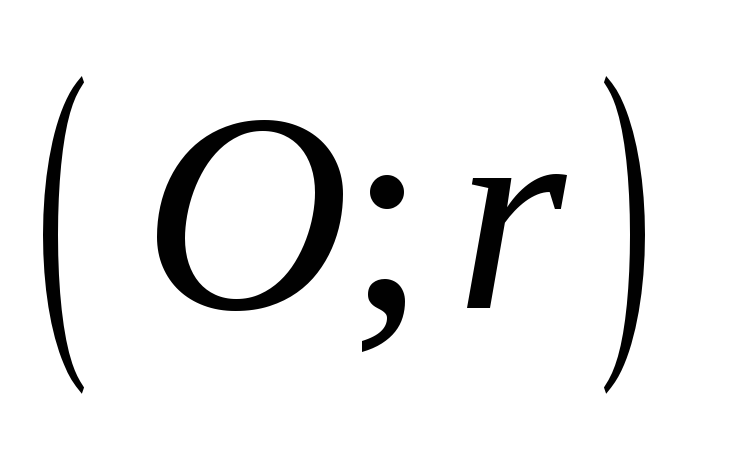 провести хорду, яка при перетині з даною
хордою
провести хорду, яка при перетині з даною
хордою
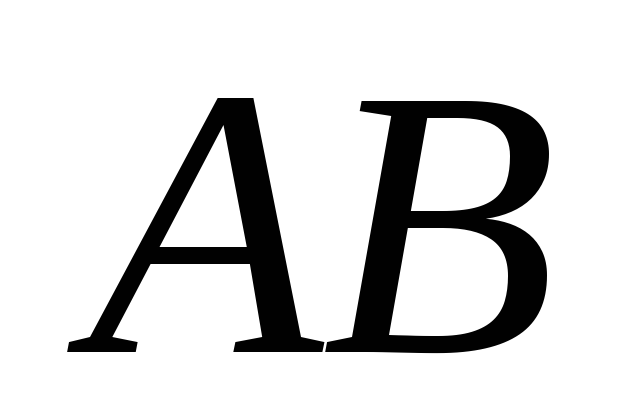 поділяється навпіл.
поділяється навпіл. -
Побудувати рівнобедрений прямокутний трикутник так, щоб вершина його прямого кута знаходилась в даній точці
 ,
а дві інші – на двох даних прямих.
,
а дві інші – на двох даних прямих. -
Побудувати трикутник, знаючи відношення його сторін
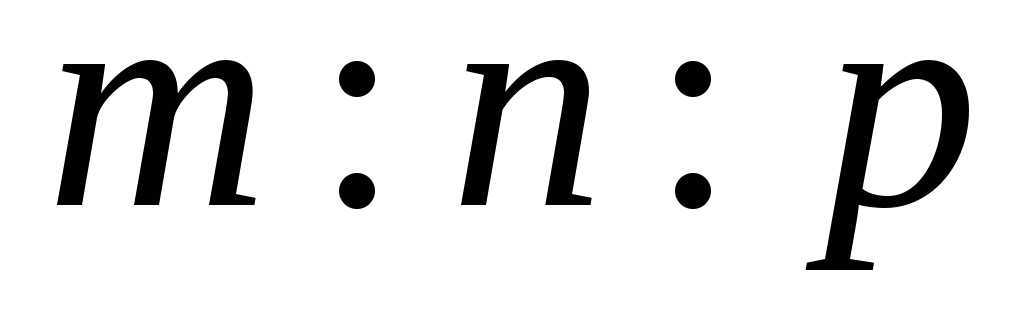 і суму основи
і суму основи
 з висотою
з висотою
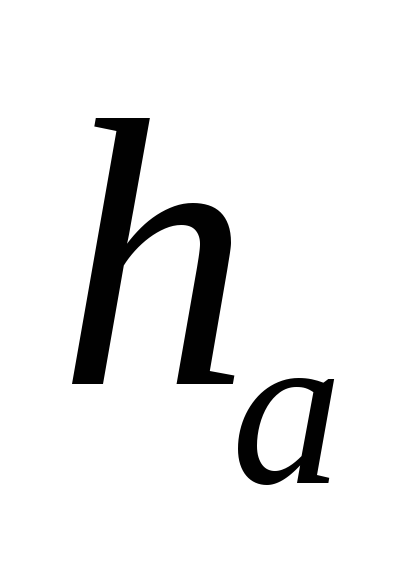 .
. -
Кола
 і
і
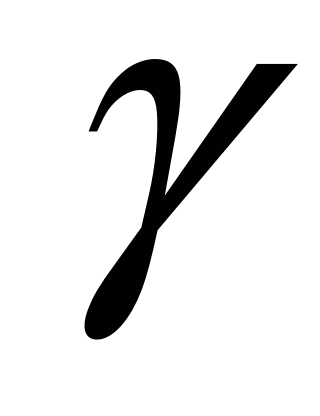 знаходяться по один бік від прямої
знаходяться по один бік від прямої
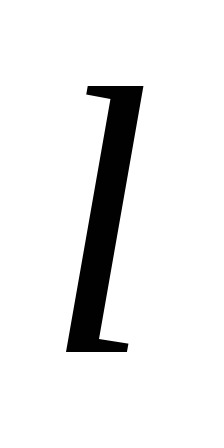 .
На прямій
.
На прямій
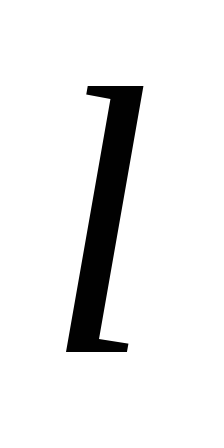 знайти таку точку, щоб дотичні, проведені
з цієї точки до даних кіл, утворювали
з прямою
знайти таку точку, щоб дотичні, проведені
з цієї точки до даних кіл, утворювали
з прямою
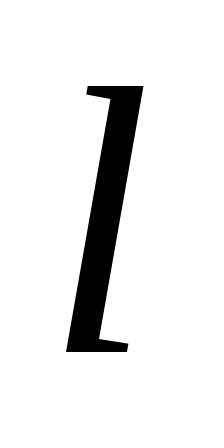 рівні
кути.
рівні
кути. -
Дано квадрат. Побудувати квадрат втричі меншої площі.
-
У трапеції
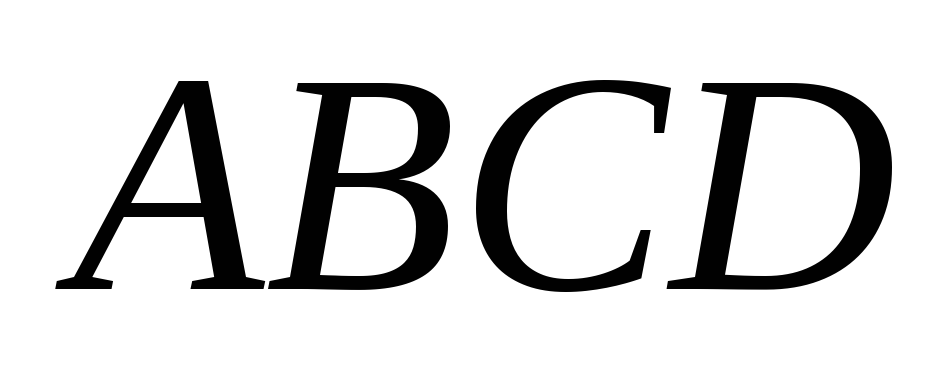 діагоналі мають довжини
діагоналі мають довжини
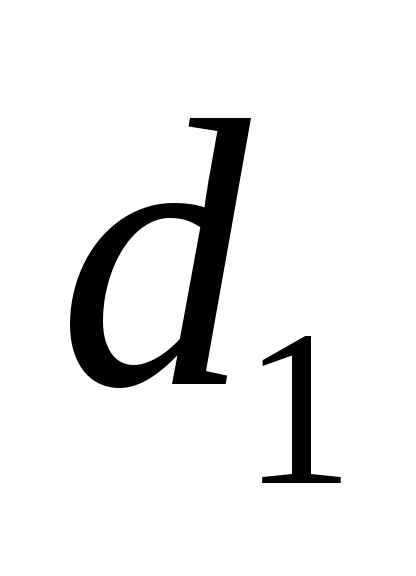 і
і
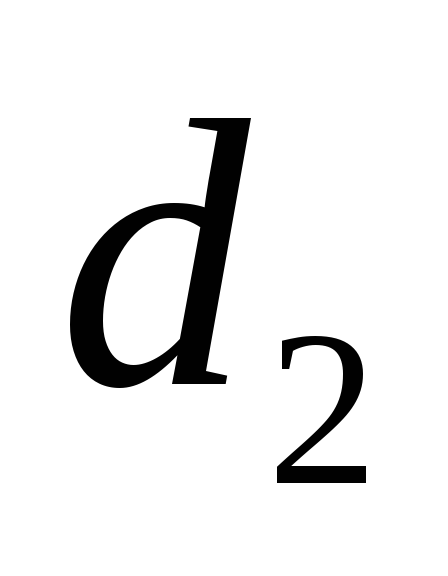 ,
,
 – кут між діагоналями,
– кут між діагоналями,
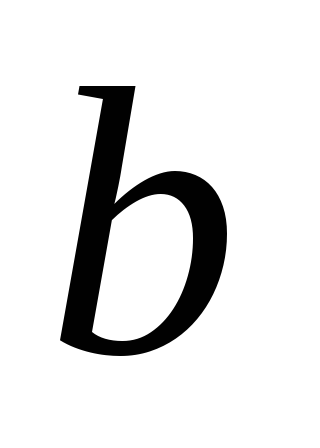 – довжина основи
– довжина основи
 .
Знайти довжину основи
.
Знайти довжину основи
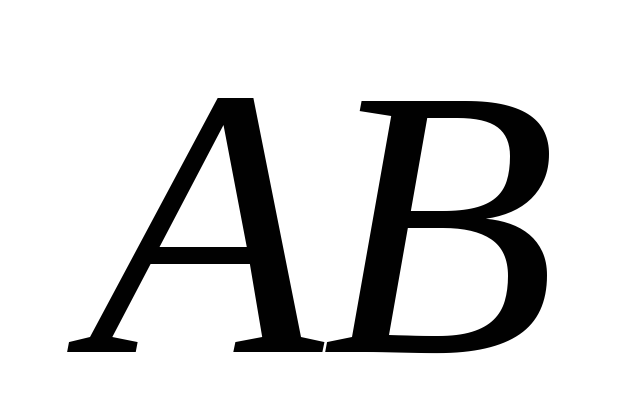 .
.
Варіант 8
-
Побудувати паралелограм за двома сторонами і кутом між діагоналями.
-
Побудувати трапецію за різницею основ, діагоналлю та двома кутами, прилеглими до однієї основи.
-
Побудувати трикутник за основою, медіаною, що проведена до основи, і кутом при вершині.
-
Побудувати квадрат, якщо дано його центр і дві точки, через які проходять дві протилежні сторони квадрата.
-
Дано кут і всередині нього точка
 .
Побудувати рівнобедрений прямокутний
трикутник, вершина прямого кута якого
співпадає з точкою
.
Побудувати рівнобедрений прямокутний
трикутник, вершина прямого кута якого
співпадає з точкою
 ,
а дві інші вершини належать сторонам
кута.
,
а дві інші вершини належать сторонам
кута. -
Даний відрізок поділити на два так, щоб більший з них був середнім пропорційним між меншим і даним відрізком.
-
У трикутник вписано коло, до якого проведені дотичні, паралельні сторонам трикутника. Довести, що протилежні сторони утвореного шестикутника рівні.
Варіант 9
-
Побудувати трапецію за одним із її кутів, двома діагоналями та середньою лінією.
-
Побудувати квадрат
 ,
знаючи його центр і дві точки
,
знаючи його центр і дві точки
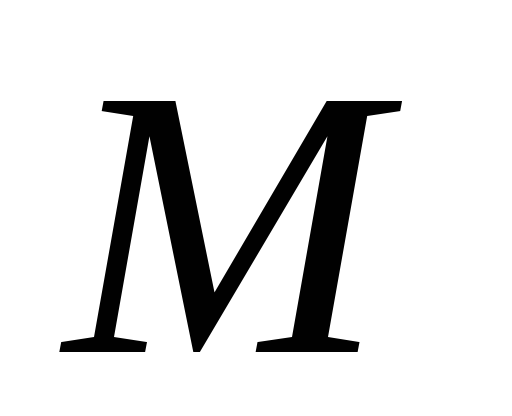 і
і
 ,
які належать прямим
,
які належать прямим
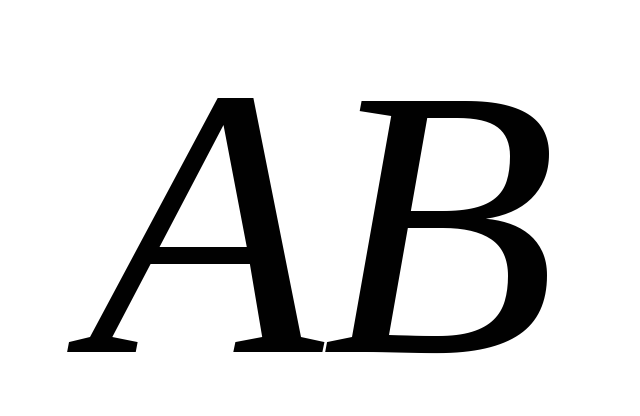 і
і
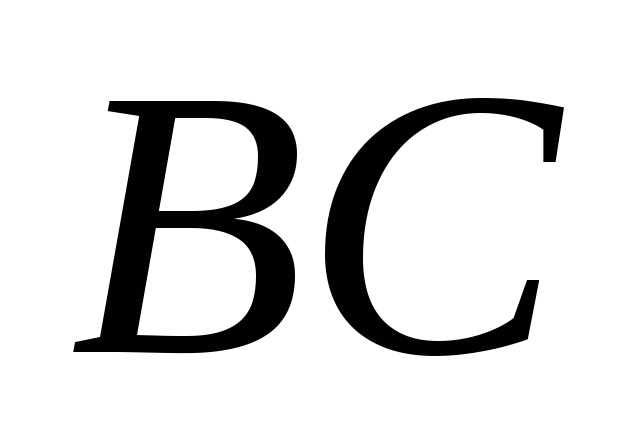 .
. -
Дано коло
 і прямі
і прямі
 і
і
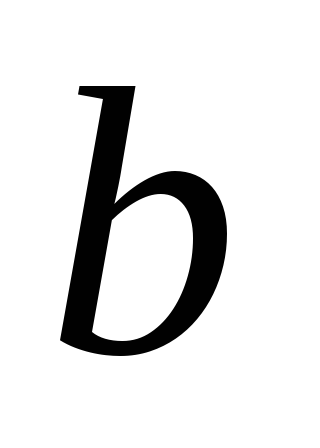 .
Побудувати рівносторонній трикутник
так, щоб одна його вершина належала
колу
.
Побудувати рівносторонній трикутник
так, щоб одна його вершина належала
колу
 ,
друга – прямій
,
друга – прямій
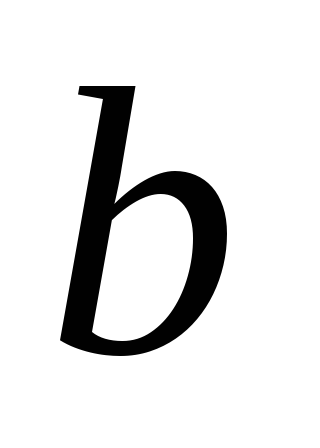 ,
а висота, що проходить через третю
вершину, – прямій
,
а висота, що проходить через третю
вершину, – прямій
 .
. -
Побудувати
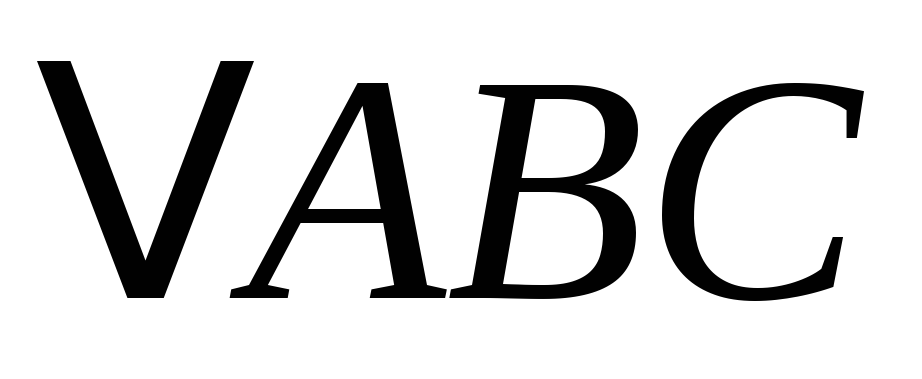 ,
знаючи кут А
, основу
,
знаючи кут А
, основу
 і різницю квадратів двох інших сторін:
і різницю квадратів двох інших сторін:
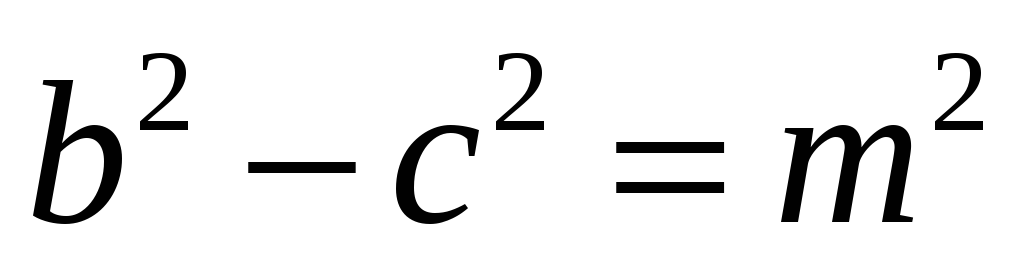 (відрізок
(відрізок
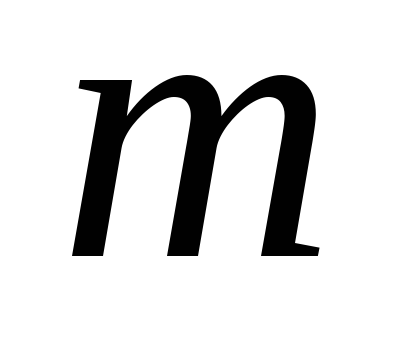 дано).
дано). -
Дано кут АОВ і всередині нього точку
 .
Побудувати на ОВ
точку М
, рівновіддалену від ОА
і точки С
.
.
Побудувати на ОВ
точку М
, рівновіддалену від ОА
і точки С
. -
Побудувати квадрат за різницею діагоналі та сторони.
-
Дано чотирикутник
 з прямими кутами
з прямими кутами
 і
і
 .
Довести, що точки
.
Довести, що точки
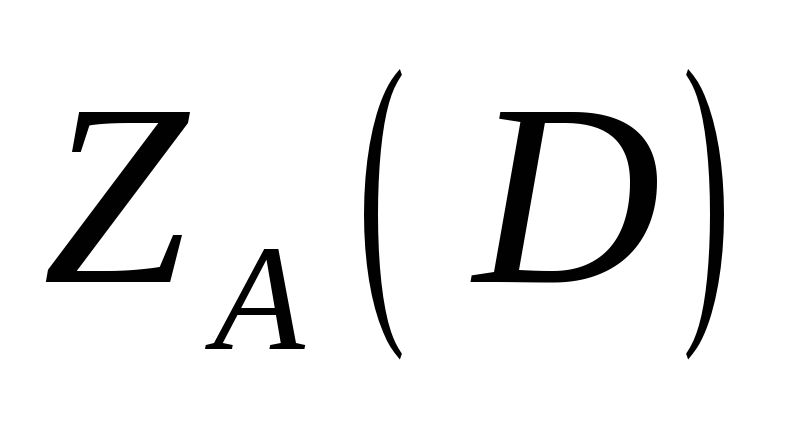 i
i
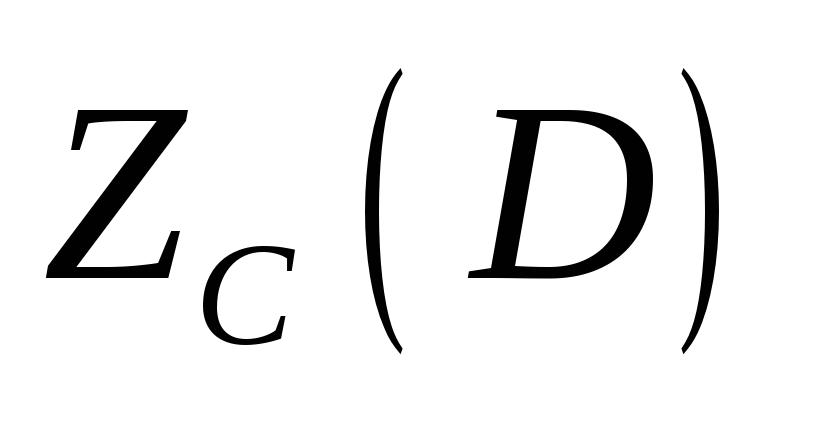 симетричні відносно ортоцентра
симетричні відносно ортоцентра
 трикутника АВС
.
трикутника АВС
.
Варіант 10
-
Вписати в дане коло трикутник, у якого відома сума двох сторін і кут, протилежний одній із цих сторін.
-
Дано відрізок. Побудувати рівний і паралельний йому відрізок так, щоб кінці його знаходились на двох даних колах.
-
Знайти та побудувати геометричне місце точок площини, сума квадратів відстаней яких до двох даних точок є сталою величиною.
-
Побудувати трикутник за двома кутами і радіусом вписаного кола.
-
Побудувати ромб так, щоб одна його діагональ була рівна даному відрізку
 і належала даній прямій
і належала даній прямій
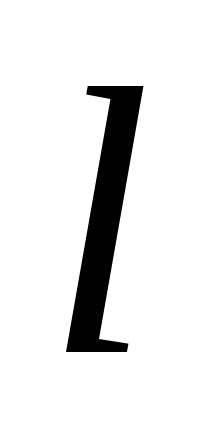 ,
а дві інші вершини – відповідно двом
даним прямим
,
а дві інші вершини – відповідно двом
даним прямим
 і
і
 .
. -
Побудувати відрізок
 ( відрізок
( відрізок
 дано).
дано). -
На сторонах паралелограма поза ним побудовані правильні трикутники. Довести, що їх центри є вершинами паралелограма.
