Алгоритм знаходження рівнянь обвідної в параметричному вигляді

Перший крок. Диференціюємо рівняння сім’ї кривих за змінним параметром, розглядаючи решту величин, що входять до рівняння, як сталі.

Другий крок. Розв’язуємо здобуте рівняння і дане рівняння сім’ї кривих відносно х і у. Знайдений результат і являтиме собою параметричні рівняння обвідної.

Зауваження. Щоб подати рівняння обвідної у прямокутних координатах, параметр а слід виключити з розглядуваних параметричних рівнянь.

Знайти обвідну сім’ї прямих

(44)

де а — змінний параметр.

^●Диференціюючи (44) за а, дістаємо

(45)

Помноживши (44) на соs a і (45) на sin a та віднявши (45) від (44), знайдемо

Аналогічно, виключаючи х із (44) і (45), записуємо

Параметричні рівняння обвідної набирають вигляду

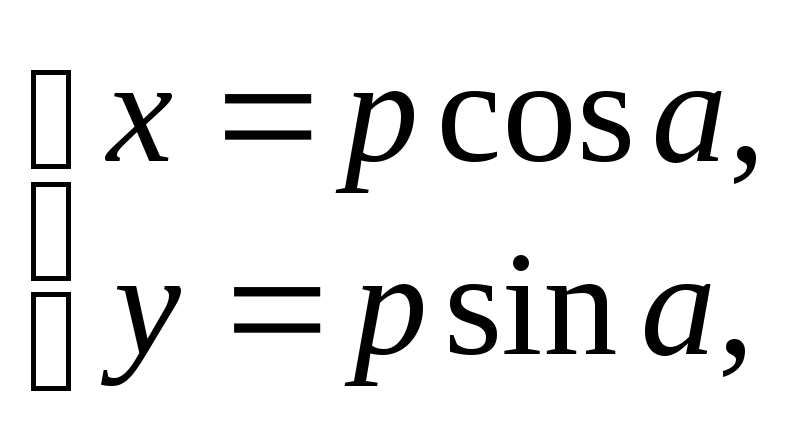(46)

де а — параметр. Піднісши обидві частини рівнянь системи (46) до квадрата і додавши почленно утворені рівності, знайдемо рівняння

, яким подається обвідна у прямокутних координатах. Це є рівняння кола, зображеного на рис. 1.33.

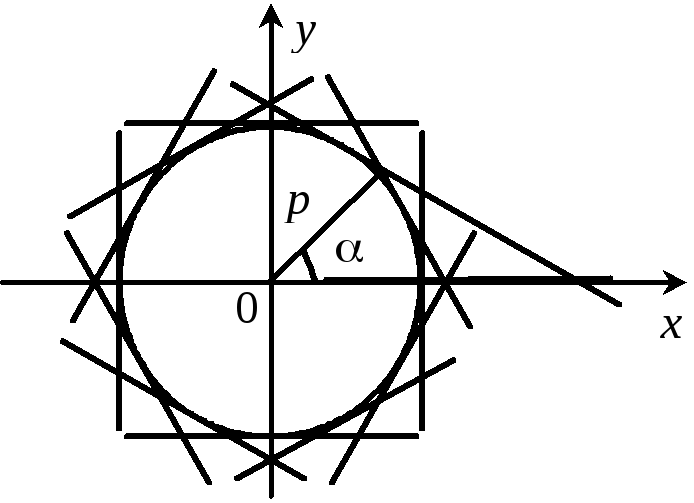
Рис. 1.33

94