1.3.12. Нормаль до поверхні

Означення. Нормаллю до поверхні в даній точці називається пряма, що проходить через цю точку перпендикулярно до дотичної площини до поверхні в цій точці.

Косинуси кутів між осями координат та будь-якою прямою, перпендикулярною до дотичної площини (32), пропорційні до

.

Отже, рівняння нормалі до поверхні в точці (х₁, у₁, z₁) подається у вигляді

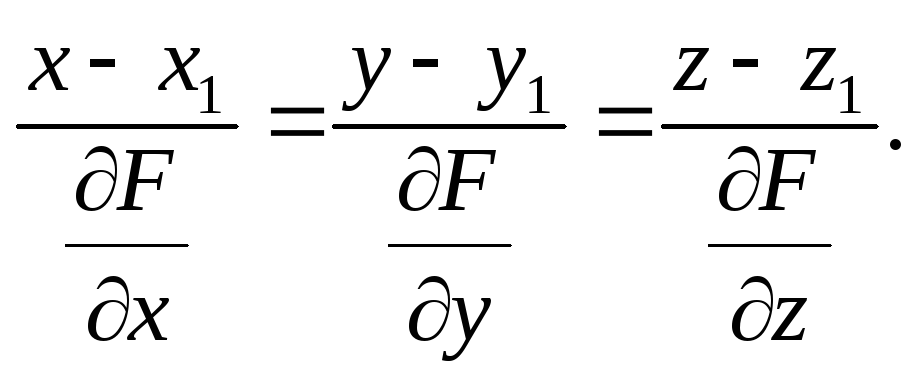(37)

Аналогічно згідно з (33) записуємо рівняння нормалі до поверхні z = f(x, y) у точці (х₁, у₁, z₁):

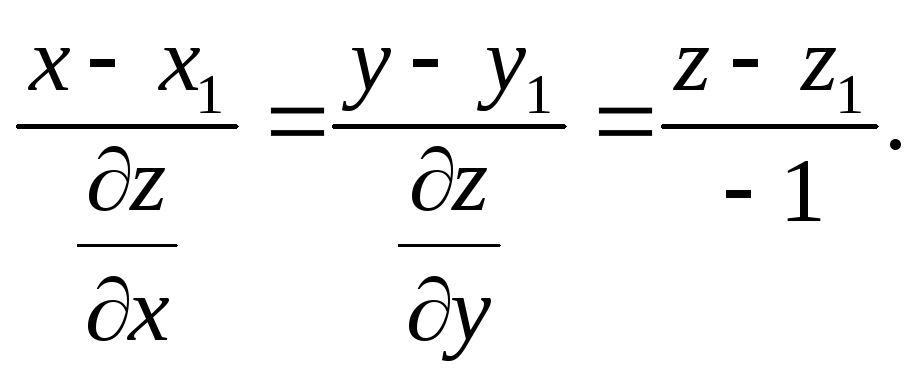
Знайти рівняння дотичної до площини і рівняння нормалі до сфери х² + у² + z² =14 в точці (1, 2, 3).

^●Нехай

,

звідки

;

х₁ = 1, у₁ = 2, z₁ = 3,

а тому

Підставляючи ці значення в (32), знаходимо рівняння дотичної площини:

або

підставляючи їх у (37), дістаємо рівняння нормалі:

,

z = 3x i 2z = 3y.

1.3.13. Обвідні

Рівняння кривої в загальному вигляді, крім змінних х і у, містить деякі сталі, від яких залежать розміри, вигляд і положення цієї кривої. Наприклад, рівнянням

(38)

подається коло, центр якого лежить на осі х на відстані а від початку координат, а розміри залежать від радіуса r.

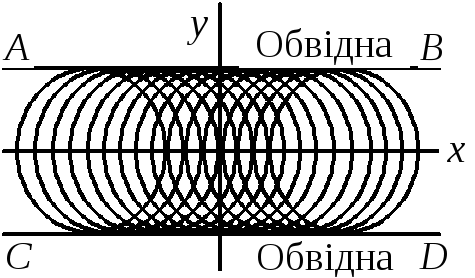
Якщо а набуває послідовно різних значень, то утворюється низка кіл, що різняться своїми відстанями від початку координат (рис. 1.32).

Рис. 1.32

Означення. Утворювану так множину кривих називають сім’єю кривих. Величина а, що є сталою для будь-якої окремої кривої, але змінною в разі переходу від однієї з таких кривих до іншої, називається змінним параметром.

Як буде показано далі, можливі й такі задачі, в яких зазначених параметрів два або більше.

Наведену щойно множину кіл називають сім’єю, що залежить від одного параметра. Коли а входить до рівняння кривої як змінний параметр, його вносять у функціональний символ, записуючи

f(x, y, a) = 0.

Усі криві сім’ї можуть дотикатися до однієї або кількох ліній (рис. 1.32). Таку криву (або кілька кривих) називають обвідною розглядуваної сім’ї. Подамо спосіб знаходження рівняння обвідної сім’ї кривих.

Нехай криву задано рівняннями в параметричній формі:

(39)

причому вона дотикається до кожної з кривих сім’ї:

f(x,y,a) = 0, (40)

а параметр а один і той самий у рівняннях (39) та в рівнянні (40).

Тангенс кута нахилу дотичної до кривої (39) у будь-якій її точці подається у вигляді

;

тангенс кута нахилу дотичної до кожної з кривих (40) визначається відношенням:

.

Отже, якщо криві (39) і (40) дотикаються одна до одної, то швидкості їх зростання в точках дотику (для одного й того самого значення а) мають бути однаковими:

,

або

(41)

За означенням, при будь-якому значенні а крива (39) дотикаєть­ся до відповідних цьому значенню кривих сім’ї (40). Тому для кож­ного значення а координати (х, у), що визначаються рівнянням (39), мають задовольняти рівняння відповідної кривої (40). Звідси випливає, що для всіх значень а справджується рівність:

(42)

утворювана підставлянням значень х і у з рівняння (39) в рівняння (40).

Отже, повна похідна лівої частини (42) за а має дорівнювати нулю для кожного значення а:

де

.

Беручи до уваги співвідношення (41), дістаємо:

(43)

Звідси випливає, що координати точок обвідної задовольняють рівняння (40) і (43):

і

тобто параметричні рівняння обвідної можна знайти, розв’язавши рівняння (38) відносно х і у. Тоді х і у визначаються як функції параметра а.