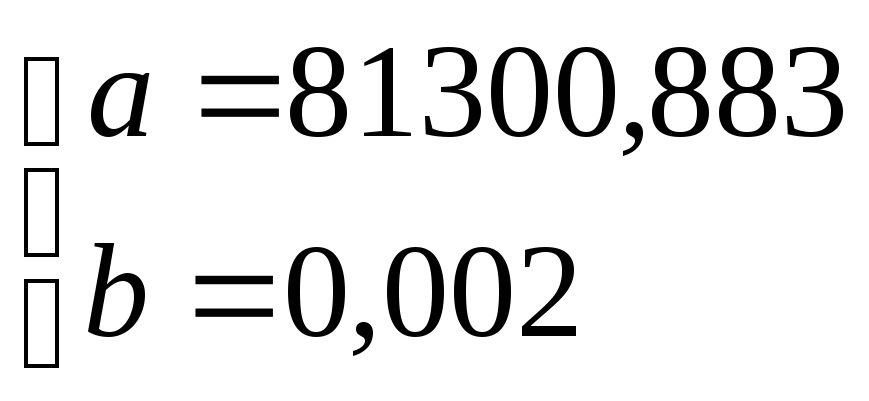8. Групповая таблица.
|
Группы
банков по величине активов, тыс. руб.
|
Число
банков
|
Средняя
балансовая прибыль данной группы
банков
|
|
12001150 –
15220748
|
10
|
229655,8
|
|
15220748
– 18440346
|
9
|
654344,7
|
|
18440346 –
21659944
|
5
|
363068,8
|
|
21659944 –
24879542
|
3
|
599568,7
|
|
24879542 –
28099140
|
3
|
532624,7
|
|
28099140 –
31318738
|
4
|
638410,0
|
|
31318738 - 34538336
|
2
|
688852,0
|
|
Итого:
|
36
|
-
|
Вывод: по таблице видно, что четкая
зависимость между факторным (величина
активов) и результативным (балансовая
прибыль) показателями отсутствует.
Поле корреляции. Эмпирическая линия
регрессии.
X – величина активов
Y – величина прибыли
Вывод: точки корреляционного поля хотя
и расположены слева направо, размещены
хаотично, а эмпирическая линия приближается
к кривой – это значит, что значения
результативного признака изменяются
неравномерно, а значение прочих неучтенных
факторов велико.
10. Построим уравнение регрессии.

Воспользуемся критерием метода наименьших
квадратов:

Частные производные функции S(a,b)=0,
отсюда получим:

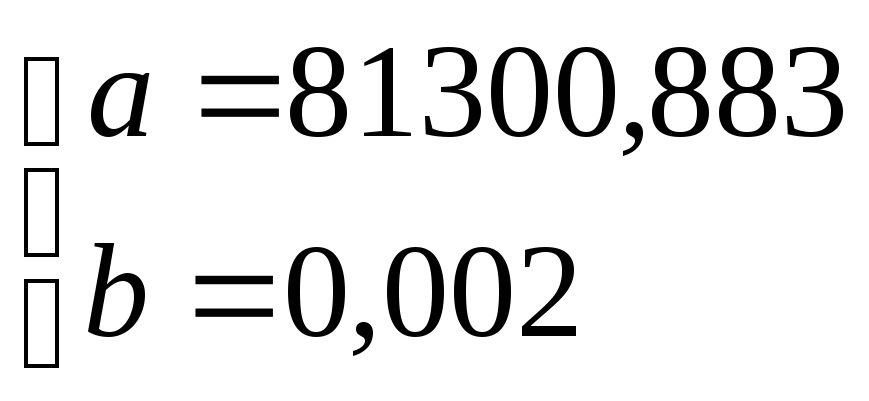
Вывод: коэф-т регрессии b=0,002,
значит имеется прямая корреляционная
зависимость. При изменении активов на
1000 руб величина прибыли меняется на 2
рубля.
Коэффициент эластичности:

Вывод: при росте активов на 1% прибыль
вырастет на 0,083 %
β-коэффициент

Вывод: если величина активов меняется
на величину СКО, то прибыль меняется на
0,018 СКО.
11