elementarna_matematyka / _ндив_дуальн_ завдання / 6 ᥬ

Міністерство освіти і науки, молоді та спорту України Полтавський національний педагогічний університет імені В.Г. Короленка

Фізико-математичний факультет Кафедра математики

ЕЛЕМЕНТАРНА МАТЕМАТИКА Індивідуальні завдання

МОДУЛЬ А (6 семестр)

для студентів ІV курсу

напряму підготовки 6.040201 „Математика”

Полтава – 2011

2

Тема 1. Трикутники

1.У прямокутному трикутнику проведена бісектриса СD прямого кута С.

Відомо, що AD = m і BD = n. Знайти висоту, опущену з вершини кута С.

2.Катети прямокутного трикутника дорівнюють b і c. Знайти довжину бісектриси прямого кута.

3.Знайти третю сторону трикутника, якщо дано дві його сторони a і b і

відомо, що медіани, проведені до цих сторін перетинаються під прямим кутом.

4.Дано два трикутники, площа кожного з яких 50 cм2 . Основа першого з них на 10 см більша основи другого. У яких межах може змінюватися основа першого трикутника, щоб різниця висот трикутників, проведених до цих

основ, була не менша 5см?

6

5.Бісектриси AM і BN трикутника ABC перетинаються в точці O. Відомо, що

AO=3MO, NO= 3 1 BO. Знайти кути трикутника ABC.

6. У рівнобедреному трикутнику ABC кут при основі 45 , а площа S.

Знайти площу трикутника, вершинами якого є основи висот трикутника

ABC.

7.У рівнобедреному трикутнику довжина основи дорівнює а, довжина висоти, опущеної на основу, дорівнює h. Знайти відстань від середини основи до бічної сторони.

8.У прямокутному рівнобедреному трикутнику через вершину прямого кута проведено дві прямі, які розбивають цей кут на три рівних кути. Знайти довжини відрізків, на які ці прямі розіб'ють гіпотенузу, якщо довжина її дорівнює а.

9.Точка М лежить на стороні АВ трикутника АВС і АВ = 3АМ. Точка К лежить на продовженні сторони АС за точку С, АК = 2АС. Знайти, у якому відношенні пряма МК ділить відрізок ВС.

4

10. Точки M і N лежать на бічних сторонах AB і BC рівнобедреного трикутника

ABC, AM 2 ABі CN 1 BC . Знайти, у якому відношенні відрізок MN ділить

3 4

висоту трапеції BD.

11.У прямокутному трикутнику АВС з гіпотенузою АВ медіани СМ і ВК

перпендикулярні. Знайти довжини всіх трьох медіан, якщо АВ = с.

12.У прямокутному трикутнику гіпотенуза рівна 10 см, висота, проведена з вершини прямого кута, дорівнює 3 см. Знайти відрізки, на які бісектриса прямого кута ділить гіпотенузу.

13.У трикутнику АВС проведена висота ВD. Через точку D проведена пряма паралельно стороні АВ до перетину зі стороною ВС у точці К. Знайти

трикутника АВС.

14. У рівнобедреному трикутнику АВС (АВ = ВС) висота AF перетинає висоту

BD у точці O, причому BO n. У якому відношенні бісектриса AE ділить

OD

висоту BD ?

15.З вершини A трикутника ABC проведені бісектриси внутрішнього і зовнішнього кутів, які перетинають пряму BC у точках D і E відповідно.

Визначити відношення AB , якщо BD 3 .

AC BE 5

16.Точка Е лежить на стороні АС правильного трикутника АВС, точка К –

середина відрізка АЕ. Пряма, яка проходить через точку Е перпендикулярно АВ, і пряма, яка проходить через точку С перпендикулярно ВС, перетинаються у точці D. Знайти кути трикутника

ВКD.

17.У трикутнику АВС перпендикуляр, що проходить через середину сторони

АВ, перетинає пряму АС у точці М, а перпендикуляр, який проходить через середину сторони АС, перетинає пряму АВ у точці N. Відомо, що МN=ВС і

пряма МN перпендикулярна до прямої ВС. Визначити кути трикутника

АВС.

5

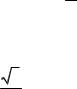
18.Два рівних правильних трикутники АВС і СDЕ зі стороною 1 розміщені на площині так, що мають одну спільну точку С і кут ВСD, менший за .

3

Точка К – середина сторони АС, точка L – середина відрізка СЕ, точка М –

середина відрізка ВD. Площа трикутника КLМ дорівнює 3 .Знайти

5

довжину відрізка ВD.

19.Дано трикутник АВС. З вершини А проведено медіану АМ, а з вершини В –

медіана ВР. Відомо, що АРВ ВМА, cos АСВ 0,8 і ВР = 1 см. Знайти площу трикутника АВС.

20.У рівнобедреному трикутнику АВС (АВ = ВС) медіана АD і бісектриса СЕ

перпендикулярні. Визначити величину кута АDВ.

6

Тема 2. Чотирикутники

21.Довжини основ трапеції дорівнюють a і b. Знайти довжину відрізка прямої,

паралельної основам трапеції, яка ділить її на дві рівновеликі фігури.

22.У прямокутнику ABCD на сторонах AB=6 і BC=8 узято точки M і N так, що відрізок MN паралельний до відрізка AC. Периметр многокутника AMNCD

відноситься до периметра трикутника MBN, як 7:3. Знайти довжину MN.

23.Визначити площу трапеції, якщо відомо, що при послідовному сполученні середин її сторін утворюється квадрат зі стороною а.

24.У трапеції довжина основи дорівнює 2а, довжини решти сторін трапеції дорівнює а. Знайти відстань від середини однієї бічної сторони трапеції до іншої бічної сторони.

25.У трапеції нижня основа у 5 разів перевищує верхню. Відрізок АВ,

паралельний основам трапеції, кінці якого лежать на бічних сторонах, у

чотири рази більше верхньої основи. Знайти, у якому відношенні відрізок

АВ ділить висоту трапеції.

26.У прямокутній трапеції бічна сторона, перпендикулярна до основ, удвічі більша меншої основи трапеції, рівної а. Діагоналі трапеції перпендикулярні. Знайти відстань між серединами діагоналей трапеції.

27.У паралелограмі проведені бісектриси його внутрішніх кутів. Площа одержаного від їх перетину чотирикутника дорівнює 25% площі паралелограма. Знайти відношення довжин сторін паралелограма.

28.Пряма, паралельна до основ трапеції, ділить її на дві частини. Площі яких відносяться, як m:n. Знайти довжину відрізка цієї прямої , що міститься між бічними сторонами трапеції, якщо довжини основ трапеції a і b.

29. На стороні AD ромба ABCD взято точку M, причому MD 3 AD і

10

BM=MC=11 см. Знайти площу трикутника BCM.

30.У паралелограмі ABCD бісектриса кута А перетинає сторону ВС у точці М,

а бісектриса кута С перетинає сторону у точці N. Площа чотирикутника,

7

утвореного перетином бісектрис АМ і СN з відрізками ВN і DМ, дорівнює

1,2 см2 . Знайти кути паралелограма, якщо АВ=3см і AD=5см.

31.Площа трапеції ABCD дорівнює S, а відношення основ AD : ВС = 2.

Відрізок МN розміщений так, що він паралельний діагоналі ВD, перетинає діагональ АС, а відрізок АМ паралельний до відрізка СN. Визначити длощу чотирикутника АМND, якщо СN : АМ=3, ВD: МN=6.

32.Один з кутів трапеції дорівнює 30 , а бічні сторони при продовженні перетинаються під прямим кутом. Знайти меншу бічну сторону трапеції ,

якщо її середня лінія дорівнює 10 см, а менша основа - 8 см.

33.У трапеції більша основа дорівнює 5 см. Одна з бічних сторін дорівнює

3см. Відомо, що одна з діагоналей перпендикулярна заданій бічній стороні,

а інша ділить кут між заданими бічною стороною і основою пополам.

Знайти площу трапеції.

34.Бічна сторона трапеції і відрізок перпендикуляра, проведеного на цю сторону з середини іншої бічної сторони,дорівнюютьa іb. Визначити площу трапеції.

35.Основи рівнобічної трапеції дорівнюють 3см і 12 см. Визначити відстань між точками перетину діагоналей трапеції з відрізками, які сполучають кінці меншої основи з серединою більшої.

36.Площа трапеції дорівнює Q, а відношення її основ дорівнює k . Знайти площі трикутників, утворених основами і відрізками діагоналей трапеції.

37.У паралелограмі діагоналі дорівнюють d1 і d2 d1 d2 , а гострий кут між сторонами дорівнює . Знайти площу.

38.Знайти діагоналі трапеції, якщо її середня лінія дорівнює 7см, висота

дорівнює 15 3 см і кут, під яким видно основи трапеції з точки перетину її

7

діагоналей, становить 120 .

39.Висота рівнобічної трапеції дорівнює h, а кут між її діагоналями,

протилежний бічній стороні, дорівнює . Знайти середню лінію трапеції.

40.Кут при вершині А трапеції ABCD дорівнює . Бічна сторона АВ удвоє більше від меншої основи ВС. Знайти кут BAC.

8

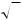
Тема 3. Комбінації многокутників

кутом CBF розташовані так, що точки E і F лежать на продовженні сторони

AD за точку D. Площа чотирикутника DBCE складає 75% площі паралелограма. Знайти гострий кут ромба.

42.Вершини К, Н, Е прямокутника КВНЕ лежать відповідно на сторонах АВ,

СD, АD рівнобічної трапеції ABCD з основами ВС і АD. Знайти кути трапеції, якщо ВН=5ВК, BC 0,6AE .

43.Трапеція AEFG з основами EF і AG розміщена в квадраті ABCD зі стороною 14 см. Точки E, F, G лежать на сторонах AB, BC, CD відповідно.

Діагоналі трапеції перпендикулярні і EG=102 см. Знайти периметр трапеції.

44.У чотирикутнику АВСD гострий кут між діагоналями дорівнює . Через кожну вершину проведено пряму, перпендикулярно до діагоналі, яка не містить цю вершину. Визначити відношення площі чотирикутника,

обмеженого цими прямими, до площі чотирикутника АВСD.

45.У паралелограмі АВСD кут ВАD дорівнює . Нехай О – довільна точка

всередині паралелограма, О1 , О2 , О3 , О4 - точки, симетричні точці О відносно прямих АВ, ВС, СD, АD відповідно. Визначити відношення площі чотирикутника О1О2 О3 О4 до площі паралелограма.

46.У прямокутний рівнобедрений трикутник АВС з прямим кутом при вершині В вписано прямокутник МNКВ так, що дві його сторони МВ і КВ

лежать на катетах, а вершина N – на гіпотенузі АС. В якому відношенні точка N повинна ділити гіпотенузу АС, щоб площа прямокутника складала

18% площі трикутника ?

47.У прямокутний рівнобедрений трикутник АВС з кутом В 90 вписано прямокутний трикутник МNС, так що MNC 90 , точка N лежить на гіпотенузі АС, а точка М – на стороні АВ. В якому відношенні точка N

9

повинна ділити гіпотенузу АС, так що площа трикутника МNС складала

3 від площі трикутника АВС ?

8

48.Знайти відношення площі правильного п'ятикутника до площі трикутника,

утвореного стороною п'ятикутника і двома його діагоналями, які виходять з кінців цієї сторони.

49.Протилежні сторони опуклого шестикутника АВСDEF попарно паралельні і рівні. Яку частину площі шестикутника становить площа трикутника АСE

?

50.Точки М і – середини сторін СD і DА паралелограма АВСD. Прямі АМ і ВN

перетинаються у точці Р. Яку частину площі даного паралелограма становить площа трикутника АNР ?

51.У трикутнику АВС з вершини А проведено пряму, яка перетинає сторону

стороні ВС між точками В і D взято точку Е так, що DЕ=СD, і через неї проведено пряму, паралельну стороні АС, яка перетинає сторону АВ у

точці F. Знайти відношення площ трапеції АСEF і трикутника АDС.

52.Дано паралелограм АВСD, у якого АВ=1, ВС=2, ABC - тупий. Через кожну з точок В і D проведено по дві прямі, з яких одна перпендикулярна до сторони АВ, а друга перпендикулярна до сторони ВС. У перетині цих

чотирьох прямих утворюється паралелограм, подібний до паралелограма

АВСD. Знайти площу паралелограма АВСD.

53.У квадрат зі стороною а вписано прямокутник так, що на кожній стороні квадрата лежить вершина прямокутника. Обчислити діагональ прямокутника, якщо його площа дорівнює S.

54.На сторонах рівнобедреного прямокутного трикутника з катетом b назовні побудовані квадрати. Центри цих квадратів сполучено між собою відрізками. Знайти площу утвореного трикутника.

10