
- •Аналітична геометрія
- •Завдання № 1 Вектори. Дії над векторами
- •Завдання № 2 Скалярний добуток векторів
- •Завдання № 3 Векторний добуток векторів
- •Завдання № 4 Мішаний добуток векторів
- •Завдання № 5 Застосування векторного методу до розв’язування задач
- •Завдання № 6 Афінна та прямокутна декартова системи координат на площині
- •Завдання № 7 Полярна система координат
- •Завдання № 8 Пряма на площині
- •Завдання № 9 Метричні задачі з теорії прямих
- •Завдання № 10 Задачі з теорії прямих
- •Завдання № 11 Коло і пряма
- •Завдання № 12 Застосування координатного методу до розв’язування задач
- •Завдання № 13 Еліпс
- •Завдання № 14 Гіпербола
- •Завдання № 15 Парабола
- •Завдання № 16 Загальне рівняння лінії другого порядку
- •Завдання № 17 Зведення загального рівняння лінії другого порядку до канонічного виду
- •Завдання № 18 Афінні перетворення
- •Завдання № 19 Рухи
- •Завдання № 20 Перетворення подібності
Завдання № 17 Зведення загального рівняння лінії другого порядку до канонічного виду
У задачах 1 – 10 звести рівняння лінії другого порядку до канонічного виду та визначити її тип. Виконати схематичний малюнок лінії.
 .
. .
. .
. .
. .
. .
. .
. .
. .
.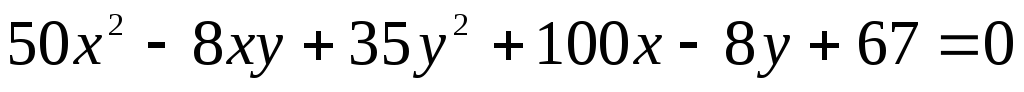 .
.
Завдання № 18 Афінні перетворення
Записати формули косого стиску в координатах у довільному афінному репері.
Записати формули перетворення косої симетрії з віссю 2х+у-2=0 і напрямком, що визначається вектором
 .
.
В ортонормованому репері записати формули зсуву з коефіцієнтом k і віссю х=0.
Записати формули афінного перетворення, яке точки А(2;1), В(-1;3), С(1;-1) переводить відповідно в точки
 .
.
Довести, що будь-які два паралелограми є афінно-еквівалентними.
Довести, що для будь-якої трапеції знайдеться їй афінно-еквівалентна рівнобічна трапеція.
Записати рівняння прямих, які є інваріантними відносно афінного перетворення, заданого формулами:

Показати, що композиція двох косих симетрій з вісями, що перетинаються, є центроафінне перетворення.
Афінне перетворення задано парою відповідних реперів
 та
та .
Для заданої точкиМ
побудувати
її образ (М).
.
Для заданої точкиМ
побудувати
її образ (М).
Афінне перетворення задано парою відповідних реперів
 та
та .
Для заданої прямоїm
побудувати її образ (m).
.
Для заданої прямоїm
побудувати її образ (m).
Завдання № 19 Рухи
Знайти координати образа точки А(2;-1) при сковзній симетрії, заданій віссю
 і вектором
і вектором .
.
Написати рівняння образа прямої
 при сковзній симетрії, заданій віссю
при сковзній симетрії, заданій віссю і вектором
і вектором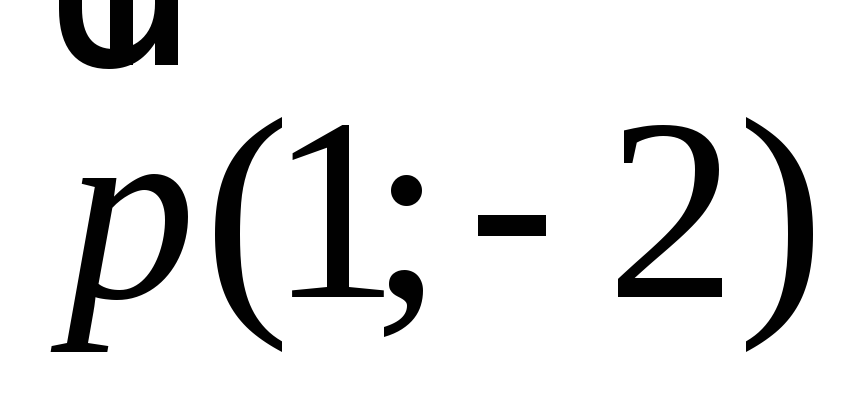 .
.
Написати рівняння образа прямої
 при повороті навколо точкиМ(2;-1)
на кут
при повороті навколо точкиМ(2;-1)
на кут
 .
.
Знайти координати образа точки А(2;2) при сковзній симетрії, заданій віссю
 і вектором
і вектором .
.
Написати рівняння образа прямої
 при сковзній симетрії, заданій віссю
при сковзній симетрії, заданій віссю і вектором
і вектором .
.
Написати рівняння образа прямої
 при сковзній симетрії, заданій віссю
при сковзній симетрії, заданій віссю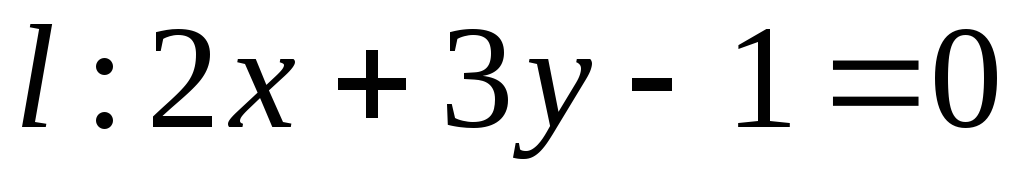 і вектором
і вектором .
.
Написати рівняння образа прямої
 при повороті навколо точкиМ(2;0)
на кут
при повороті навколо точкиМ(2;0)
на кут
 .
.
Написати рівняння образа прямої
 при повороті навколо точкиМ(1;1)
на кут
при повороті навколо точкиМ(1;1)
на кут
 .
.
Знайти образ точки М(1;2) при осьовій симетрії відносно прямої
 .
.
Знайти образ точки М(3;1) при осьовій симетрії відносно прямої
 .
.
Завдання № 20 Перетворення подібності
Довести, що якщо для трикутників АВС і
 виконуються рівності
виконуються рівності ,
то вони подібні.
,
то вони подібні.
Написати формули перетворення подібності другого роду, при якому
 ,
, .
.
Довести, що якщо для трикутників АВС і
 виконуються рівності
виконуються рівності ,
то вони подібні.
,
то вони подібні.
Медіани АК, ВN, CF трикутника АВС перетинаються в точці М. Довести, що гомотетія з центром у точці М і коефіцієнтом
 вершиниА,
В, С трикутника
переводить відповідно в точки K,
N, F.
вершиниА,
В, С трикутника
переводить відповідно в точки K,
N, F.
Використовуючи гомотетію, довести, що медіани трикутника в точці перетину діляться у відношенні 2:1, починаючи від вершини.
Довести, що якщо для трикутників АВС і
 виконуються рівності
виконуються рівності ,
то вони подібні.
,
то вони подібні.
Медіани АК, ВN, CF трикутника АВС перетинаються в точці М. Довести, що гомотетія з центром у точці М і коефіцієнтом
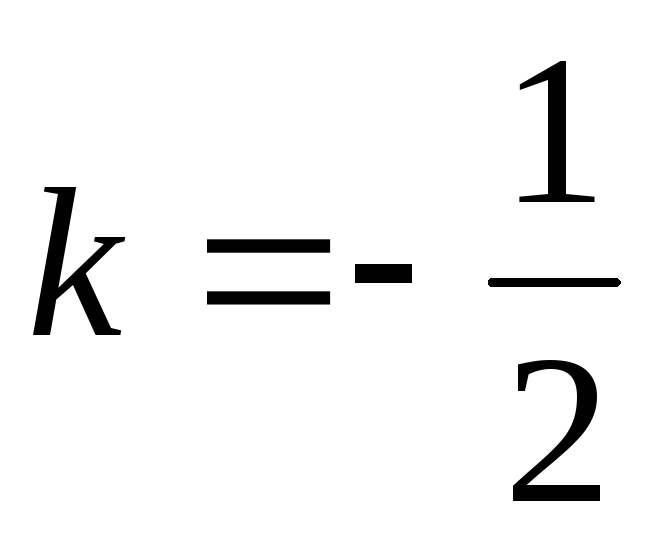 переводить сторониАВ,
ВС і АС
трикутника АВС
в середні лінії KN,
NF,
KF
відповідно.
переводить сторониАВ,
ВС і АС
трикутника АВС
в середні лінії KN,
NF,
KF
відповідно.
Використовуючи гомотетію, довести, що висоти трикутника перетинаються в одній точці.
Використовуючи гомотетію, довести, що точка перетину медіан трикутника лежить між центром описаного кола та точкою перетину висот і ділить цей відрізок у відношенні 1:2.
Написати формули перетворення подібності першого роду, при якому
 ,
, .
.

