
І рівень
-
Знайдіть невідомий член пропорції 0,(7) : х = 2,(3) : 0,(3).
-
Виконайте дії
 .
. -
Знайдіть число на яке треба поділити 3848, щоб частка дорівнювала 160, а остача дорівнювала 8.
-
Знайдіть невідомий член пропорції 3,(3) : 2,25 = 0,(4) : х.
-
Знайдіть суму чисельника і знаменника дробу, який утворюється внаслідок скорочення дробу
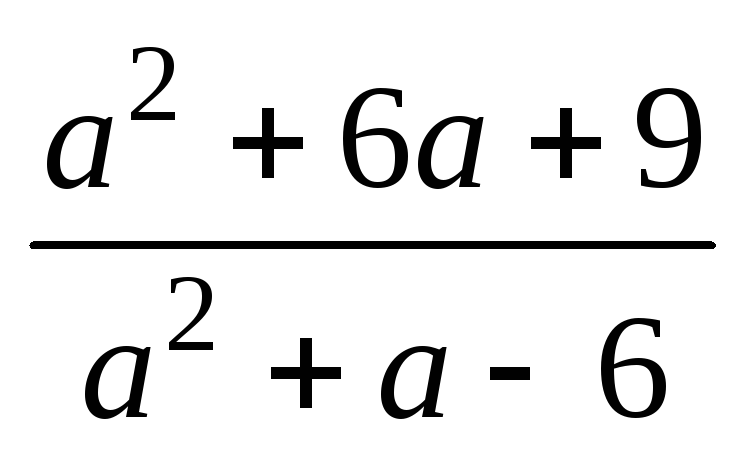 .
. -
Спростіть вираз
 якщо
якщо
 .
. -
Розкладіть многочлен 8a3 + 0,027 на множники і знайдіть їх суму.
-
Знайдіть суму чисельника і знаменника нескоротного дробу, який дорівнює дробу
 .
. -
Винесіть множник з-під знака кореня
 ,
якщо n > m > 0.
,
якщо n > m > 0. -
Розкладіть многочлен m2 – 3m – 4 на множники і знайдіть їх суму.
-
Спростіть вираз
 .
. -
Знайдіть х + у, якщо х і у задовольняють систему рівнянь

-
Пряма
 проходить через точки А
(1; –1) і В
(9; –6). Знайдіть коефіцієнти
проходить через точки А
(1; –1) і В
(9; –6). Знайдіть коефіцієнти
 і
і
 .
. -
Розв’яжіть нерівність
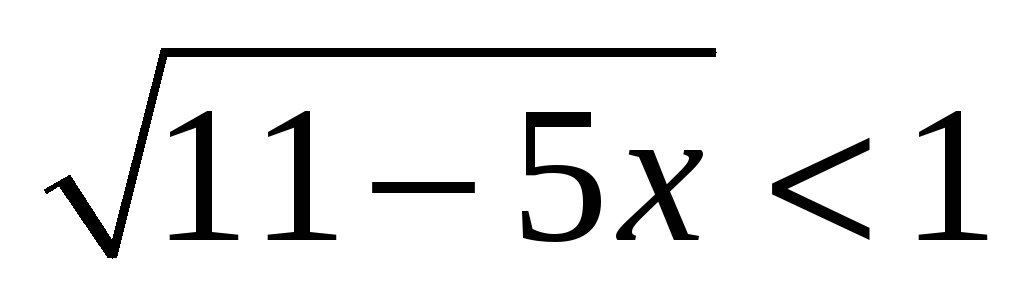 .
. -
Знайдіть модуль різниці найбільшого і найменшого цілочислових розв’язків нерівності | 3х – 2 | < 4.
-
Знайдіть цілочислові розв’язки нерівності
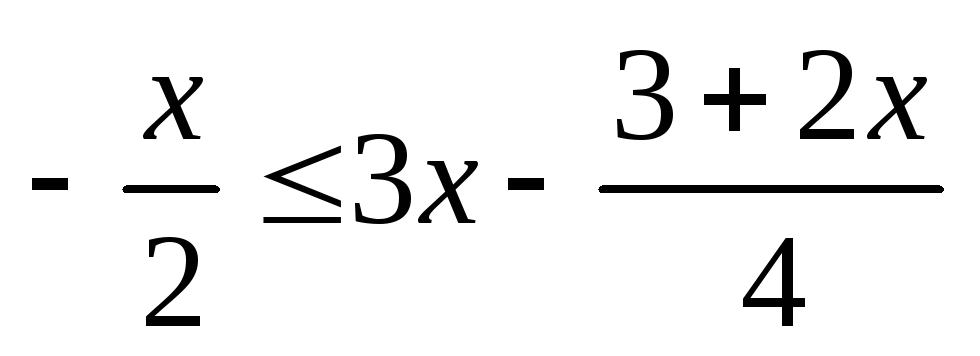 ,
що належать проміжку (–5; 5).
,
що належать проміжку (–5; 5). -
Розв’яжіть нерівність
 .
. -
Знайдіть суму всіх цілочислових розв’язків нерівності
 .
. -
Знайдіть цілочислові розв’язки нерівності
 на проміжку (5; 11).
на проміжку (5; 11). -
Знайдіть суму натуральних чисел, які задовольняють нерівність | 5 – 3х | < 5.
-
Розв’яжіть нерівність
 .
.
-
Розв’яжіть нерівність
 .
. -
Обчисліть середнє арифметичне натуральних чисел, які задовольняють нерівність
 .
.
-
Обчисліть середнє геометричне натуральних чисел, які задовольняють нерівність
 .
. -
Знайдіть кількість цілочислових розв’язків нерівності
 .
. -
Обчисліть значення функції
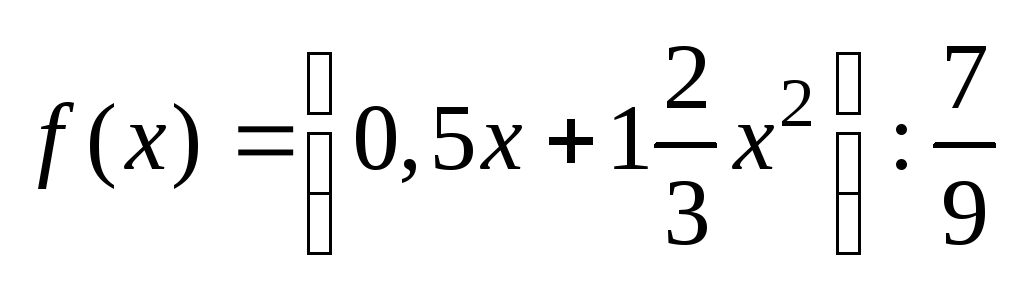 у точці x
= 6.
у точці x
= 6. -
Знайдіть область визначення функції
 .
. -
Знайти нулі функції y = (x2–7)·| x–2 |.
-
Знайдіть область визначення функції
 .
. -
Знайти точку максимуму функції y = |5 – 2x| + 7.
-
Знайдіть вершину параболи y = x2 – 5x + 1?
-
На якому проміжку функція y = |x | – 5 набуває від’ємних значень?
-
Знайдіть точку екстремуму функції y = – 4x2 + 2x –7.
-
Для яких значень x функція
 набуває додатних значень?
набуває додатних значень? -
Знайдіть область значень функції
 .
. -
Обчисліть значення виразу
 .
. -
Упорядкуйте числа a, b, c, якщо
 ,
,
 ,
,
 .
. -
Визначте знаки sin , cos і tg , якщо = 1042º.
-
Обчисліть
 .
. -
Визначте знаки sin , cos і tg , якщо
 .
. -
Скільки спільних розв’язків мають рівняння
 і
і
 на
проміжку (0; 2p) ?
на
проміжку (0; 2p) ? -
Знайдіть усі розв’язки рівняння
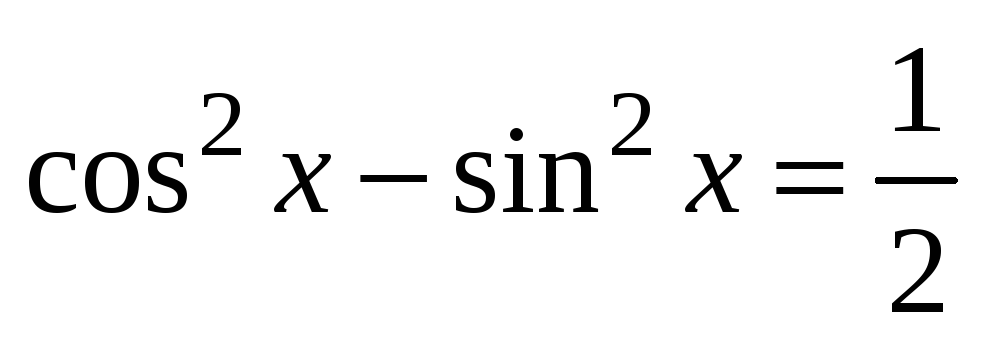 .
. -
Знайдіть розв’язки рівняння
 ,
які належать проміжку (–2p ; 3p)
?
,
які належать проміжку (–2p ; 3p)
? -
Знайдіть усі розв’язки рівняння
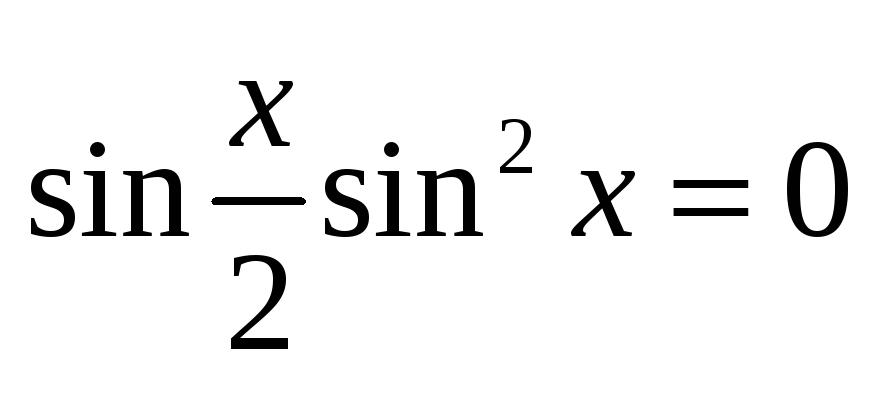 .
. -
Укажіть найбільший розв’язок рівняння
 ,
який належить проміжку (–90º; 90º).
,
який належить проміжку (–90º; 90º). -
Укажіть кількість нулів функції
 ,
які належать проміжку (–p; p).
,
які належать проміжку (–p; p). -
Розв’яжіть нерівність
 .
. -
Знайдіть х, якщо
 .
. -
Розв’яжіть нерівність
 .
. -
Знайдіть область визначення функції
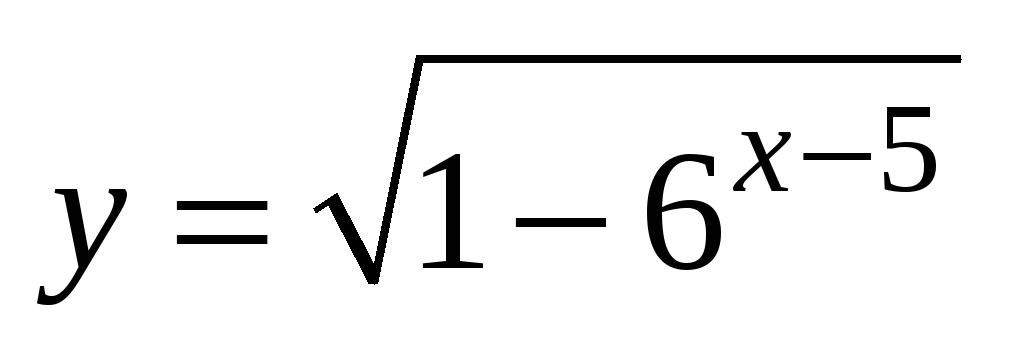 .
. -
Знайдіть, при яких значеннях х функції
 і
і
 набувають рівних значень.
набувають рівних значень. -
Розв’яжіть нерівність
 .
. -
Знайдіть значення виразу
 ,
якщо х = 0,2
і у = 0,01.
,
якщо х = 0,2
і у = 0,01. -
Розв’яжіть нерівність
 .
. -
Знайдіть, при яких значеннях х функції
 і
і
 набувають рівних значень.
набувають рівних значень. -
Знайдіть область визначення функції
 .
. -
Обчисліть перший член геометричної прогресії, якщо її третій член дорівнює 3, а четвертий дорівнює 15.
-
Послідовність задано рекурентно a1 = 2, an+1 = 3an – 1. Чому дорівнює її четвертий член?
-
Знайдіть суму перших десяти членів геометричної прогресії (bn), у якій b1 = 5, b2 =
 .
. -
Обчисліть перший член арифметичної прогресії, якщо її п’ятий член дорівнює 2, а шостий дорівнює –1.
-
Обчисліть суму всіх натуральних чисел, що не перевищують 100 і поділяються на шість.
-
Знайдіть суму нескінченно спадної геометричної прогресії (bn), якщо
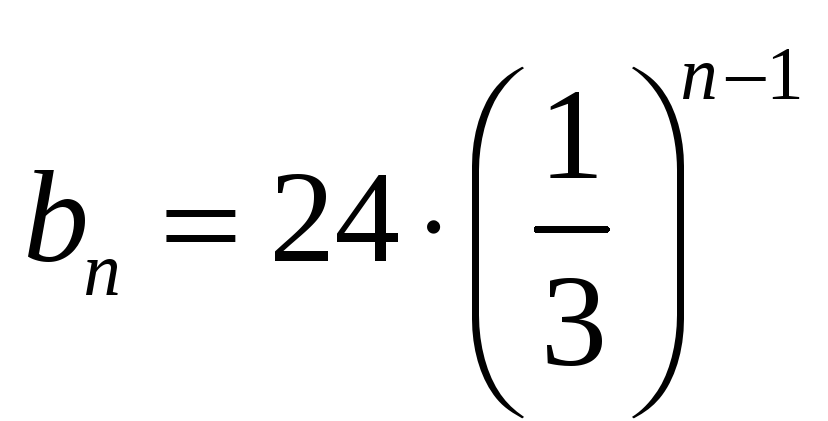 .
. -
Обчисліть перший член геометричної прогресії, якщо її сьомий член дорівнює 80, а п’ятий дорівнює 20.
-
Скільки від’ємних членів має арифметична прогресія –30; –28; –26; ...?
-
Знайдіть суму нескінченно спадної геометричної прогресії (bn), у якій b2 = 24, b3 = 8.
-
Обчисліть перший член арифметичної прогресії (an), якщо a4 = 5, a5 = 3.
-
Знайдіть суму перших десяти членів геометричної прогресії (bn), якщо
 ,
b2 = 3.
,
b2 = 3. -
Обчисліть другий член геометричної прогресії, якщо її четвертий і п’ятий члени дорівнюють 6 і 3 відповідно.
-
Обчисліть суму всіх натуральних чисел, що не перевищують 200 і кратні 13.
-
Знайдіть суму нескінченно спадної геометричної прогресії 24; 12; …
-
Обчисліть перший член геометричної прогресії, якщо її третій член дорівнює 15, а п’ятий дорівнює 3.
-
Скільки додатних членів має арифметична прогресія 20,5; 19,5; 18,5; ...?
-
Довести, що для будь-якого натурального n правильна рівність
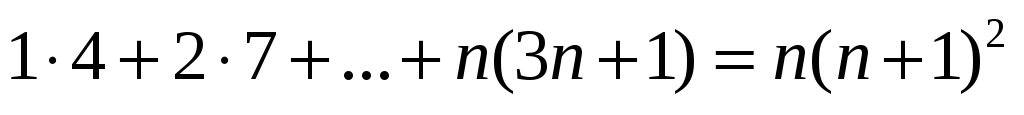 .
. -
Довести, що для будь-якого натурального n правильна рівність
 .
. -
Довести, що для будь-якого натурального n
 .
. -
Доведіть, що для будь-якого натурального n правильна рівність:
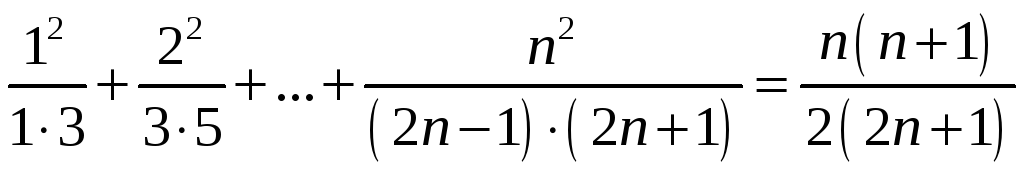 .
. -
Довести, що для будь-якого натурального n
 .
. -
Довести, що при будь-якому натуральному n (
 ) поділяється на 64.
) поділяється на 64. -
Довести, що для будь-якого натурального n
 .
. -
Довести, що для будь-якого натурального n
 .
.
