ЗАДАЧА Д 1

Интегрирование дифференциальных уравнений движения

материальной точки

Груз массой , получив в точке начальную скорость , движется в изогнутой трубе , расположенной в плоскости рисунка; участки трубы или оба наклонные, или один наклонный, а другой горизонтальный (рис. Д1.0-Д1.9, табл. Д1).

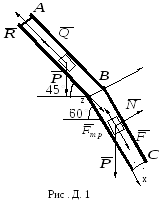
На участке на груз, кроме силы тяжести, действует постоянная сила (ее направление показано на рисунке) и сила сопротивления среды , зависящая от скорости груза (направлена против движения); трением груза о трубу на участке пренебречь.

В точке груз, не изменяя скорости, переходит на участок трубы, где на него, кроме силы тяжести, действует сила трения (коэффициент трения груза о трубу ) и переменная сила , проекция которой на ось задана в таблице.

Считая груз материальной точкой и зная расстояние или время движения груза от точки до точки , найти закон движения груза на участке , т.е. , где .

Указания. Задача Д1 - на интегрирование дифференциальных уравнений движения точки (решение основной задачи динамики). Решение задачи разбивается на две части. Сначала нужно составить и проинтегрировать методом разделения переменных дифференциальное уравнение движения точки (груза) на участке , учтя начальные условия. Затем, зная время движения груза на участке или длину этого участка, определить скорость груза в точке . После этого нужно составить и проинтегрировать дифференциальное уравнение движения груза на участке тоже с учетом начальных условий, ведя отсчет времени от момента, когда груз находится в точке , и, полагая в этот момент . При интегрировании уравнения движения на участке в случае, когда задана длина участка , целесообразно перейти к переменной , учтя, что

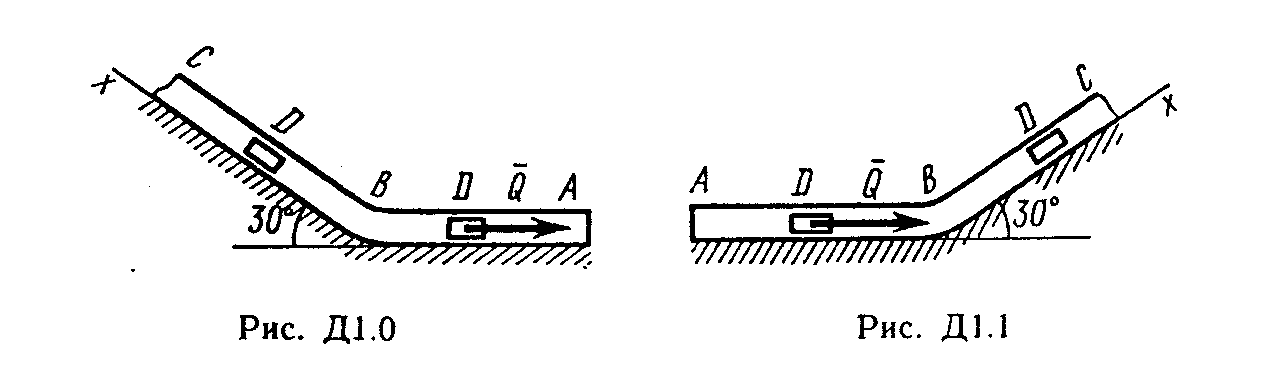
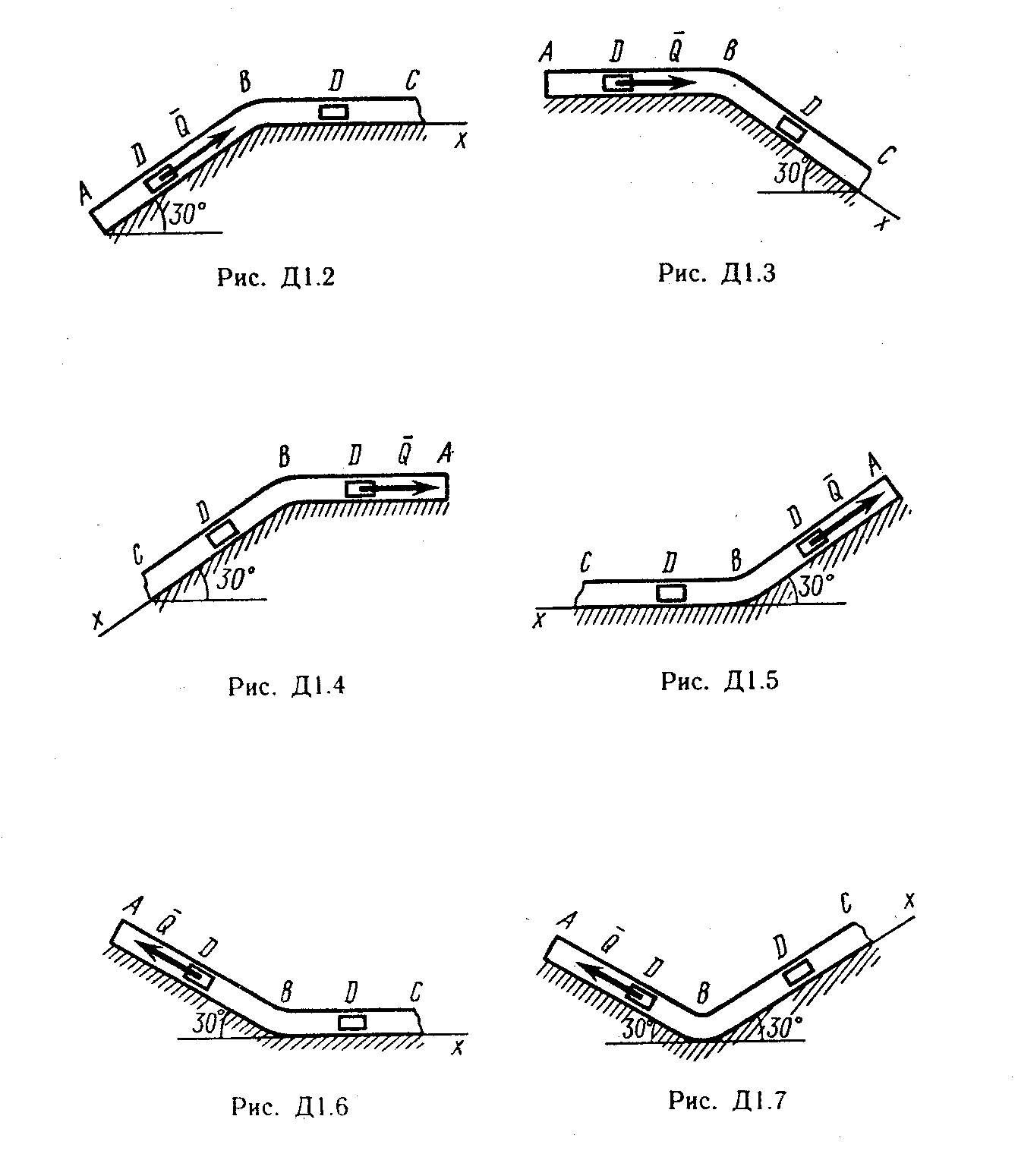
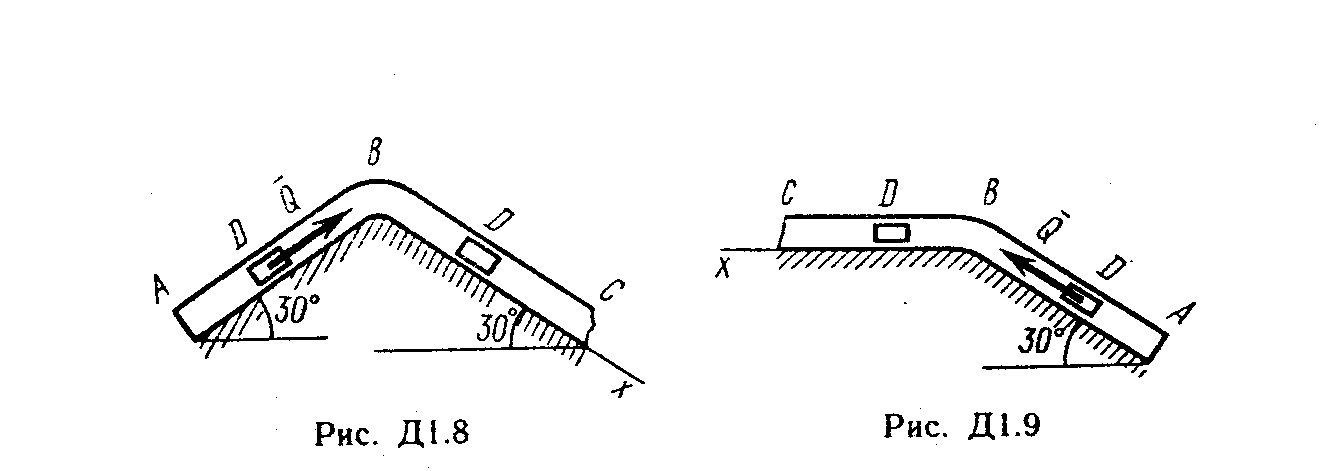
Таблица Д 1

№ усл
0	3	16	5	0.6	-	5
1	2	18	9	0.5	4	-
2	6	28	14	0.3	-	10
3	1.8	12	6	0.9	2	-
4	4.5	20	19	0.5	-	3
5	1.6	10	8	0.2	2	-
6	4,8	15	19	0,4	-	4
7	8	12	21	0,8	2,5	-
8	4	22	7	0,8	-	5
9	5	24	15	0,25	5	-

Пример Д 1. На участке трубы (рис. Д1) на груз массой действуют сила тяжести, постоянная сила и сила сопротивления ; расстояние от точки , где , до точки равно . На участке на груз действуют сила трения груза о трубу (коэффициент трения задан) и переменная сила .

Дано:

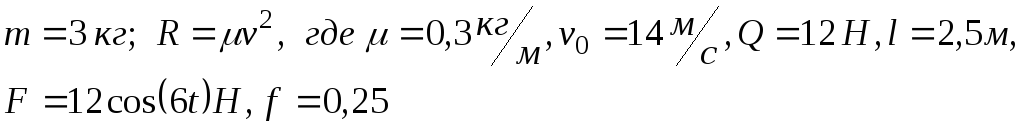
Определить: - закон движения груза на участке .

Решение. Рассмотрим движение груза на участке,считая груз материальной точкой. На него действуют силы: сила тяжести сила сопротивления движению и постоянная сила . Проведем ось в сторону движения груза и составим дифференциальное уравнение движения груза в проекции на эту ось:

Подставим значения и уравнение принимет вид:

Так как сила сопротивления пропорциональна , производим замену переменной:

Разделив обе части на и учитывая, что , получим:

или

Введем обозначения:

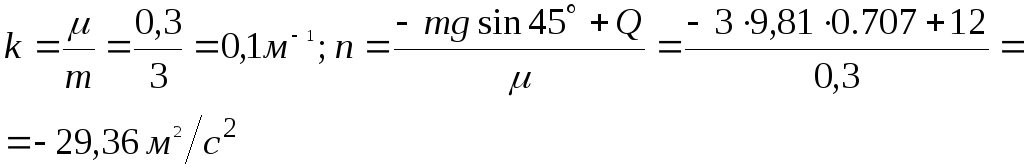
Тогда уравнения (3) можно записать в виде:

Разделим переменные:

и проинтегрируем уравнения:

Примечание. Если сила сопротивления зависит от , то замена переменной не производится и уравнение будет иметь вид:

Введем обозначения:

и ,

получим

Тогда разделим переменные:

и проинтегрируем уравнение:

________________________________________________________________

По начальным условиям при . Это означает:

и из равенства находим:

,

отсюда

Потенцируем:

Отсюда находим:

Полагая в равенстве , число и заменяя и их значениями, находим скорость груза в точке :

Рассмотрим движение груза на участке. Будем отсчитывать время от момента, когда груз находится в точке , считая в этот момент Тогда найденная скорость будет для движения на этом участке начальной скоростью (). На груз действуют силы: сила тяжести ; нормальная реакция трубы ; сила трения и переменная сила . Проведем из точки оси и составим дифференциальное уравнение движения груза в проекции на ось :

где . Для определения составим дифференциальное уравнение в проекции на ось . Так как , получим :

.

Следовательно

.

Уравнение примет вид:

Разделим обе части уравнения на :

или

Разделим переменные и проинтегрируем уравнение:

Найдем значение из начальных условий: при

При найденном значении уравнение примет вид:

Снова разделим переменные и проинтегрируем уравнение:

Постоянную интегрирования находим из начальных условий: при

Окончательно искомый закон движения груза примет вид:

,

где - в метрах, - в секундах.