TZI_RGZ_4

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ,

МОЛОДЕЖИ И СПОРТА УКРАИНЫ

ОДЕССКИЙ НАЦИОНАЛЬНЫЙ МОРСКОЙ УНИВЕРСИТЕТ

Кафедра «Информационные технологии»

Расчётно - графическое задание №4

по предмету «Технологии защиты информации»

«Открытая криптосистема RSA»

Выполнил:

ст. III курса

4 группы 3 курса КСФ

Устич А.В.

Проверила:

Чернышова И.В.

Одесса

2012

Открытая криптография

Проблемы симметричных криптосистем:

1. Передача секретного ключа.

2. Одноразовость приемника ключа.

3. Организация связи «один к одному».

4. Относительная криптостойкость.

5. Ненадежная цифровая подпись.

Создание открытой криптографии позволило решить проблемы симметричных криптосистем. Открытая система RSA строиться на 2-х взаимосопряженных ключах.

Ключ СЕКРЕТНЫЙ (личный) К^С принадлежит лишь владельцу ключа и никому не передается – решена проблема передачи секретного ключа.

Ключ ОТКРЫТЫЙ К^ОТ является общедоступным и публикуется в соответствующих справочниках.

Ключи RSA вычисляются на основе неразрешимой задачи факторинга. Она состоит в том, чтобы по известному произведению (n) вычислить факторы-факторинги p и q.

Эта задача о необратимых функциях (реализован 4-й принцип Шеннона абсолютно стойкого ключа). Факторы p и q являются ВЗАИМНО ПРОСТЫМИ числами, длинной не менее 100 цифр. Ключевое пространство настолько велико, что для взлома ключей К^С и К^ОТ понадобится более 100 лет работы Суперкомпьютера.

Таким образом ключи К^С и К^ОТ становятся ДОЛГОВРЕМЕННЫМИ (ПОСТОЯНЫМИ). Они также являются СВЕРХСТОЙКИМИ. На основе открытой криптографии создается НАДЕЖНАЯ ЭЛЕКТРОННО-ЦИФРОВАЯ ПОДПИСЬ.

Работа открытой криптосистемы

Односторонняя связь.

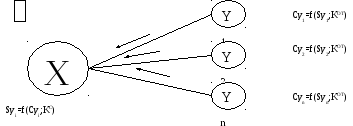
При шифровании исходника Syi открытым ключом настолько сложно, что расшифровать его не может владелец исходника.

Двухсторонняя связь

При двухстороннем обмене зашифрованными сообщениями необходимы 2 пары взаимосопряженных ключей

(;)&(;)

C_x=f(S_x;) C_y=f(S_y; )

Генерация ключей RSA

Из модульной арифметики известно, что любое целое число можно представить в виде:

Целое число а КОНГРУЭНТНО bmodn,

где n - основание модуля

b - остаток от деления а/n.

Ключи Секретный и Открытый вычисляем в несколько шагов:

1. Выбираем два взаимно простых фактора р и q (р  q).

р=5, q=7

2. Вычисляем модуль RSA.

mod RSA =

3. Вычисляем функцию Эйлера.

4. Выбираем фактор d < n – простое число (d = 7).

5. Из модульного уравнения:

вычислим параметр е

6. На основе факторов составляем ключи.

К^С={e, n}={31, 35}

К^OT={d, n}={7, 35}

1.Шифрование в RSA

Исходное сообщение S представляется в форме полинома. После возведения S в степень d отбрасывается целая часть и вычисляется остаток по модулю n. Сообщение-число не должно превышать модуля RSA. Если оно его превышает, то сообщение разбивается на блоки, каждый из которых не превышает модуля RSA и каждый блок шифруется и дешифруется. Шифрование выполняется открытым ключом.

S=ВАЛЕТ==20131875;

20131875 32

20131872 629121 32

В=3 629120 19660 32

А=1 19648 614 32

Л=12 608 19=Т

Е=6

S=20131875>mod RSA

S={S₁=В; S₂=А; S₃=Л; S₄=Е; S₅=Т}

a)

C={17; 1; 33; 6; 19}

Таким образом, исходное сообщение, разбитое на блоки, после шифрования представляет собой шифротекст, состоящий из такого же числа блоков.

2. Дешифрование в RSA

Выполняется секретным ключом.

C={27;14;30;6;6;1}

{3;1;12;6;19}={В;А;Л;Е;Т}

3.Криптостойкость

- Сверхвысокая криптостойкость

- Ключи не взламываются, т.к. их взлом связан с решением неразрешимой математической задачи факторинга.

- Ключи долговременные, постоянные.

-Открытые криптосистемы работают медленно, т.к. необходимо выполнить большой объем вычислительной работы. В системе RSA при шифровании и дешифровании необходимо возводить большие числа в большие степени.