2. Значення 

1) Обчислюємо значення при температурі 150Cза допомогою многочлена першої степені. Використовуєм дві вузлові точки: (120;933), (140;914). Багаточлен першої степені, що приймає у вузлових точках задані значення, має вид:

=деТ задана температура.

Отримаємо значення =904,5 кг/м³

2) Обчислюємо значення при температурі 150Cза допомогою многочлена другої степені. Використовуєм три вузлові точки: (100;952), (120;933), (140;914). Багаточлен другої степені, що приймає у вузлових точках задані значення, має вид:

=

де Т - задана температура.

Отримаємо значення =904,5 кг/м³

Оцінюємо похибку:

= 100% = 0%

Похибка менше 5%, отже нас задовольняє поліном першої степені.

3) Обчислюємо значення при температурі 150Cза допомогою многочлена сьомої степені.Використовуєм всі експериментальні точки:

Отримаємо значення =894,4205кг/м³

3. Значення cp

1) Обчислюємо значення c_pпри температурі 150Cза допомогою многочлена першої степені. Використовуєм. дві вузлові точки: (120;2,5116), (140;2,7837). Багаточлен першої степені, що приймає у вузлових точках задані значення, має вид:

c_p=де Т- задана температура.

Отримаємо значення c_p =2,9197 кДж/(кг)

2) Обчислюємо значення c_pпри температурі 150Cза допомогою многочлена другої степені. Використовуєм три вузлові точки: (100;2,3232), (120;2,5116), (140;2,7837). Багаточлен другої степені , що приймає у вузлових точках задані значення, має вид:

c_p=

де Т - задана температура.

Отримаємо значення c_p=2,9511 кДж/(кг). Оцінюємо похибку:

=100%= 1,075%

Похибка менше 5%, отже нас задовольняє поліном першої степені.

3) Обчислюємо значення c_pпри температурі 150Cза допомогою многочлена сьомої степені.Використовуєм всі експериментальні точки:

Отримаємо значення c_p=2,8743. кДж/(кг)

5.4 Зворотня інтерполяція

Для визначення температури при відомому параметрі ми використовуємо метод зворотньої інтерполяції (по формулі Лагранжа): використовуємо ту ж саму прикладну програму lagrang.exe; вводимо число вузлових точокN= 2 (n=N-1), але, вводячи попарноxтаy, просто міняємо їх місцями.

Отримаємо многочлени для розрахунків з використанням двох найблищих вузлових точок.Отримуемо многочлен першої степені:

T_{ = 0,0022}==

Ввод:

Х1=2,3-е 03 У1=40

Х2=1,5-е 03 У1=60 Шукане Х=2,2-е 03

Розрахункове значення:

T_{ = 0,0022}=45,5000C

Отримаємо многочлени для розрахунків з використанням трьох найблищих вузлових точок Отримуемо многочлен другої степені:

Т_{ =0,0022}=

Ввод:

Х1=2,3-е 03 У1=40 Х3=1,1-е 03 У1=80

Х2=1,5-е 03 У1=60 Шукане Х=2,2-е 03

Розрахункове значення:

Т_{ =0,0022}=41,0417C

Оцінюємо похибку:

=100%=4,8%

Отримаємо многочлени для розрахунків з використанням двох найблищих вузлових точок. Отримуемо многочлен першої степені:

T _{Ср = 2,40}=

Ввод:

Х1=2,3232 У1=100

Х2=2,5116 У1=120 Шукане Х=2,4

Розрахункове значення:

T_{Ср = 2,40}=108,1529C

Отримаємо многочлени для розрахунків з використанням трьох найблищих вузлових точок Отримуемо многочлен другої степені:

Т _{Ср = 2,40}=

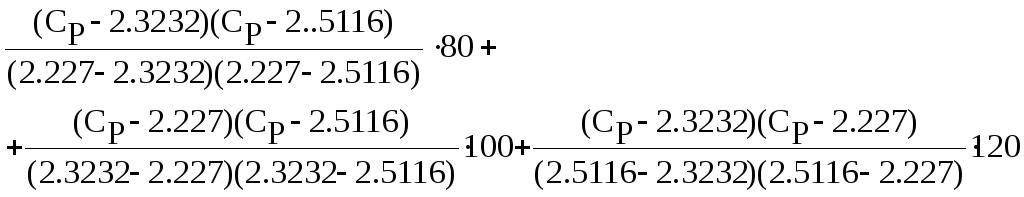
Ввод:

Х2= 2,3232 У2=100 Х1=2,2270 У1=80

Х3=2,5116 У3=120 Шукане Х=2,4

Розрахункове значення:

T_{Ср = 2,40}=111,2169C

=100%=2,8%

Отже і в першому і другому випадках нас задовольняє поліном першої степені, так як похибка менше 5%.

Таблиця 14

Узагальнююча таблиця методів інтерполяції

Температура	Параметри	Параболічна інтерполяція	Метод Лагранжа
		n =1	n =1	n =3
25C		3,5281(n =2)	3,5281(n =2)	3,6622
		1018,25	1018,25	1019,2325
	cp	2,08515	2,0836	2,0833
85C		1,025	1,025	1,0191
		967	967	965,1525
	cp	2,2510	2,2510	2,2456
150C		0,214	0,215	-0,1414
		904,515	904,5	894,4205
	cp	2,919	2,9197	2,8743