3. Найпростіші правила інтегрування

1.За властивістю 3 невизначеного інтеграла отримуємо перше правило інтегрування: постійний множник можна виносити з-під знака інтеграла.

2. З властивостей 3,4 невизначеного інтеграла витікає друге правило: невизначений інтеграл від суми (різниці) функцій , дорівнює сумі (різниці) інтегралів від цих функцій (тут припускається, що первісні для функцій , існують).

3. Не існує загального правила обчислення інтеграла від складної функції. Винятком є лише випадок, коли складна функція містить лише два рівні вкладеності, до того ж внутрішня функція є лінійною, тобто

,

де — зовнішня, а — внутрішня функції. Тоді

,

де .

Дійсно:

.

Таким чином, для обчислення первісної у цьому випадку треба:

а) знайти первісну для зовнішньої функції ;

б) замінити аргумент в первісній на внутрішню лінійну функцію ;

в) домножити отриману функцию на , де — кутовий коефіцієнт внутрішної функції .

Приклад 1. .

Підінтегральний вираз є сумою трьох функцій: , , . Кожна з цих функцій є неперервною скрізь на множині дійсних чисел , а тому, за основною теоремою інтегрального числення, має первісну на будь-якому інтервалі з . Це дає можливість скористуватися правилами 1 і 2 для обчислення інтегралу:

Приклад 2. .

Підінтегральний вираз представимо в вигляді степеневої функції: . Користуючись формулою 3 ТОНІ, отримаємо:

.

Приклад 3. .

.

Приклад 4. .

Підінтегральний вираз представляє дріб. Правила інтегрування дробу, на відміну від диференціювання, не існує. Але якщо розділити почленно чисельник дроба на знаменник, отримаємо під знаком інтеграла суму степеневих функцій, інтегрування яких не визиває труднощів.

.

=

Приклад 5. Проінтегрувати многочлен , де — степень многочлена, в загальному вигляді.

Приклад 6. .

Хоча підінтегральний вираз є складною функцією, яка містить лише два рівні вкладеності, внутрішня функція не є лінійною, тому ми не можемо користуватися правилом 3.

Скористуємося для підінтегральної функції формулою скороченого множення:

.

Отримаємо:

.

Тоді за правилами 1,2 і формулами 2,3 ТОНІ, отримаємо

=

.

Приклад 7. .

Інтеграл не є табличним. Підінтегральну функцію розглянемо як складну функцію .

,

де зовнішня функція , а внутрішня — — лінійна. За правилом 3 спочатку знаходимо первісну для зовнішньої функції, користуючись формулою 4 ТОНІ:

.

Замість в підставляємо :

.

Оскільки кутовий коефіцієнт в лінійній внутрішній функції дорівнює 2, треба домножити отриману функцію на :

.

Взагалі:

(3.1)

Приклад 8. Аналогічно прикладу 7, отримуємо, що

Приклад 9. .

Підінтегральна функція є складною дворівневою функцію, для якої зовнішня функція — , а внутрішня — — є лінійною. Користуємося правилом 3. За допомогою формули 8 ТОНІ знаходимо первісну зовнішньої функції.

Аналогічно за допомогою формули 7 ТОНІ отримаємо, що:

Приклад 10. .

Розкриємо дужки в чисельнику підінтегральної функції і поділимо чисельник на знаменних почленно:

Інтегрування дробу зі складним знаменником часто полегшується розкладанням його на суму дробів з більш простими знаменниками. Наприклад,

.

Користуючись таким розкладанням дуже просто отримати, наприклад, формулу 18 ТОНІ:

Для дробу загального виду має місце рівність:

,

з якої отримаємо

(3.2)

Формула (3.2) дає простий спосіб для обчислення інтегралів від функцій виду , де . Для цього треба розкласти знаменник на множники: , де — це корені рівняння .

Приклад 11. .

Оскільки коефіцієнт при в знаменнику підінтегральної функції дорівнює 1, для рішення рівняння скористуємося теоремою Вієта: сумма коренів дорівнює 5, а добуток 6. Корені — 2,3.

.

Приклад 12. .

.

4.Метод заміни змінної. В основі метода наступне зауваження: якщо відомо, що

,

то .

Всі функції припускаються неперервними.

Нехай потрібно обчислити інтеграл

.

У багатьох випадках вдається в якості нової змінної вибрати таку функцію , щоб підінтегральний вираз можна було представити у вигляді:

,

де — більш зручна для інтегрування функція, ніж .Тоді достатньо знайти інтеграл

,

щоб з нього підстановкою отримати шуканий інтеграл.

Простіше всього заміна проводиться тоді, коли у поданому виді підінтегрального виразу в якості множника вже присутня похідна від нової змінної (хоча так буває далеко не завжди). Наступні 13 прикладів розглядають саме такі випадки.

Приклад 13. .

Підінтегральний вираз поряд з містить у якості множника . Це говорить на користь заміни: .

.

І взагалі для інтегралів виду

, , ,

(3.3)

доцільно використовувати заміни

, , ,

відповідно, оскільки в поданих підінтегральних виразах присутні похідні від нових змінних (можливо, з точністю до знака).

Приклад 14. .

Поданий інтеграл є інтегралом вида (3.3) (другий з наведених), підінтегральний вираз має вигляд , де , тому робимо заміну змінної:

.

Приклад 15. .

Шуканий інтеграл не є табличним і, з першого погляду, не має виглял (3.3), але якщо пригадати, що , то стає очевидним, що підінтегральна функція — це , де , а тому

Отже

Взагалі, якщо шуканий інтеграл має вигляд

,

так що в підінтегральному виразі чисельник є диференціалом знаменника, заміна зразу приводе до цілі:

.

(3.4)

Приклад 16. .

Чисельник у шуканому інтегралі з точністю до постійного множника представляє похідну знаменника:

,

тому для обчислення інтегралу скористуємося формулою (3.4):

.

Приклад 17. .

Обчислення інтегралу проведемо, користуючись формулою (3.4), спочатку перетворивши підінтегральну функцію за допомогою тригонометричних перетворень:

.

Тепер чисельник функції явно представляє собою похідну знаменника, а тому за формулою (3.4):

(3.5)

Приклад 18. .

При перетворенні підінтегрального виразу за допомогою тригонометричної формули приведення:

та відповідної заміни змінної, приходимо до інтегралу, розглянутого в попередньому прикладі:

Отримали формулу, зручну для використання при обчисленні інтегралів:

(3.6)

Якщо інтеграл має вигляд

(3.7)

то він береться за допомогою підстановки

Приклад 19. .

Інтеграл має вигляд (3.7), де , тому

.

Приклад 20. .

Підінтегральний вираз представляє добуток складної функції , для якої внутрішня функція є квадратичною, і лінійної . Пригадаємо, що при обчисленні похідної від степеневої функції показник степені зменьшується на 1, тобто похідна від квадратичної функції буде лінійною: . Таким чином, в підінтегральному виразі, з точністю до сталого множника, вже присутня похідна від — . Не вистачає множника 6. Введемо його в підінтегральний вираз штучно:

.

Тепер корисною буде заміна :

.

Взагалі для інтегралів виду

(3.8)
доцільною є заміна

оскільки множник в підінтегральному виразі відрізняється від лише постійним коефіцієнтом . Таким чином

.

Приклад 21. .

Для того, щоб спростити підінтегральний вираз, зауважимо, що при диференціюванні аргументу функції отримаємо: , що відрізняється лише постійним множником від чисельника. Це робить корисною для спрощення підінтегральної функції заміну: .

.

Приклад 22. .

Для інтегрування треба спростити підінтегральний вираз. Наявність множника у чисельнику наштовхує на думку про доцільність заміни виду: . Для шуканого інтегралу у якості квадратичної функції для заміни змінної має сенс розглянути . Дійсно

.

Приклад 23. .

Порівнюючи показники степені при у чисельнику і знаменнику підінтегральної функції, для спрощення виразу приходимо до доцільності заміни: .

.

Приклад 24. .

.

Цей самий інтеграл можна було обчислити, роблячи іншу заміну, яка приводе до більшого спрощення підінтегральної функції:

.

Приклад 25. .

Для обчислення інтегралів такого типу пропонується спочатку поділити чисельник і знаменник підінтегрального дробу на . Це приведе інтеграл до виду (3.3) ():

.

Тут . Робимо запропоновану вище для такого інтеграла заміну:

Далеко не завжди у поданому виді підінтегрального виразу у якості множника вже є присутньою похідна від нової змінної. У цьому випадку корисна заміна видна не так добре. При проведенні підстановки треба добре пам'ятати, що після заміни в підінтегральному виразі скрізь повинна залишитися тільки нова змінна.

Приклад26 . .

Дуже часто, коли підінтегральний вираз містить радікал

,

доцільною є заміна

,

завдяки чому

.

Приклад 27 . .

Якщо інтеграл містить радікал

,

доцільно зробити заміну змінної

.

Тоді

.

Приклад 28 . .

Якщо інтеграл містить радікал

,

доцільно зробити заміну змінної

.

Тоді

.

;

.

Тоді

.

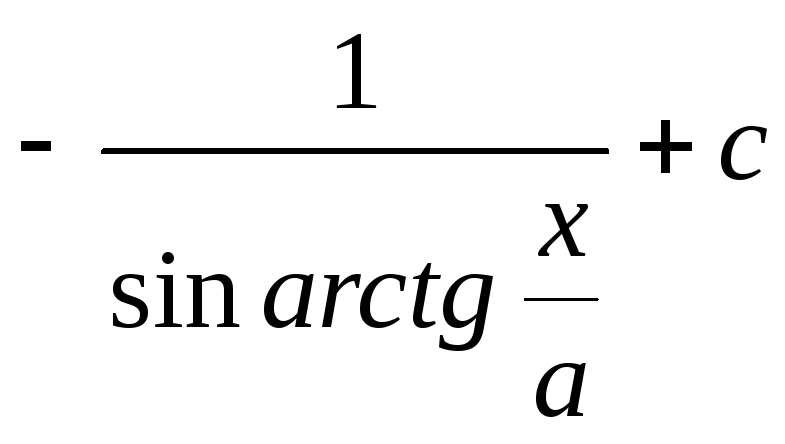Приклад 29 . .

5.Интегрування за частинами. Нехай функції визначені і диференційовані на , — неперервні на , і функція має первісну на цьому інтервалі. Тоді функція також має первісну на і виконується рівність:

, (3.9)

чи, враховуючи, що , а , формулу (3.9) можна записати в еквівалентному вигляді:

. (3.10)

Формули (3.9), (3.10) називаються формулами інтегрування за частинами.

Метод інтегрування за частинами часто використовується у випадках, коли підінтегральний вираз у якості множників одночасно містить: степеневу () і тригонометричну (і т.д.) функції; степеневу і зворотну тригонометричну (і т.д.); показникову () і тригонометричну; логарифмічну і тригонометричну (чи зворотну тригонометричну) і т.д.

Приклад 30. .

Підінтегральний вираз містить три множники: . Як розбити цей вираз на частки і , які фігурують у правій частині (3.10)? Ясно, що множник може опинитися лише в , а для двох інших множників можливі варіанти: , тоді , чи , тоді . Розглянемо обидва варіанти.

. (3.11)

Треба відмітити, що при відновленні функції за допомогою операції , достатньо взяти лише одну первісну. В нашому прикладі ми обираємо в конкретному вигляді: , а не в загальнім виді: . Довільна стала при обчисленні невизначеного інтегралу враховується в остаточному його виразі.

Зроблена розбивка підінтегрального виразу на частки привела до значного його спрощення — табличного інтегралу в правій частині (3.11). Таким чином:

. (3.12)

Подивимось, як вплине на складність обчислень інший варіант розбивки, згаданий вище:

(3.13)

Формула інтегрування за частинами використовується взагалі з метою спрощення підінтегрального виразу, але, як видно з правої частини (3.13), в даному випадку ми не спростили, а ускладнили інтеграл. Зрозуміло, що з двох можливих варіантів розбивки треба обирати перший.

Таким чином, при використанні для обчислення невизначеного інтегралу формули інтегрування за частинами, треба враховувати, що та частина підінтегрального виразу, яка увійде в множник в лівій частині (3.10), під час інтегрування диференціюється, а та частина, що входе до , інтегрується. Отож, треба розділити підінтегральний вираз поданого інтеграла на частки так, щоб виконання згаданих операцій привели до його спрощення в правій частині (3.10), а не до ускладнення.

Правило інтегрування за частинами має більш обмежену область застосування, ніж заміна змінної. Але є цілі класи інтегралів, наприклад,

де — многочлен степені , які обчислюються саме за допомогою інтегрування за частинами, але можливо, що цією формулою треба буде скористуватися декілька разів.

Приклад 31. .

Для розбивки підінтегрального виразу на корисні частки пригадаємо, що для функції похідна і первісна будуть відрізнятися лише постійними множниками, тому, з точки зору простоти і результатів проміжкових обчислень, не має значення, де опиниться : в чи в . Але для степеневої функції інтегрування приведе до зростання показника степені, на відміну від диференціювання, тому недоцільним буде розмістити в . Таким чином,

. (3.14)

Інтеграл в правій частині (3.14) не є табличним, але він простіший за поданий інтеграл: показник степеня при в підінтегральному виразі зменшився на 1. Для отриманого інтеграла ще раз скористуємося формулою інтегрування за частинами:

Нарешті,

.

Приклад 32. .

На перший погляд здається, що функція повинна опинитися в частині , щоб при диференціюванні зменшився на 1 показник степені. Але в такому випадку: , і для відновлення треба буде обчислити , який сам по собі є достатньо складним. Тому спробуємо інший спосіб розбивки:

Двократне застосування формули інтегрування за частинами привело нас до табличного інтегралу .

Для обчислення інтегралів виду

,

де — многочлен степені , формулою інтегрування за частинами треба скористуватися послідовно разів. Розбиваючи підінтегральний вираз на частки і в черговому інтегралі, в розміщуємо послідовно ,, ,...,.

Приклад 33. .

Для функцій похідна відрізняється від первісної лише постійним множником, тому не має значення в яку частину, чи , віднести кожну з цих функцій. Розглянемо один з можливих способів:

. (3.15)

Отриманий в правій частині (3.15) інтеграл за змістом ніяк не відрізняється від поданого. Застосуємо до нього формулу інтегрування за частинами:

(3.16)

Як видно з правої частини (3.16), ми знову повернулися до поданого інтеграла:

. (3.17)

Формула (3.17) дає нам лінійне рівняння відносно шуканого інтеграла, з якого отримаємо:

,

(3.18)

Аналогічно отримуємо, що

(3.19)

Приклад 34.

Виведемо рекурентну формулу для обчислення інтегралів за допомогою методу інтегрування за частинами:

.

Останній інтеграл можна перетворити наступним чином:

.

Підставляючи цей вираз в попередню рівність, отримаємо співвідношення:

.

Розвязуючи останню рівність відносно , отримаємо:

(3.20)

Формула (3.20) є рекурентною формулою для обчислення інтегралів виду . Вона зводить обчислення до обчислення інтегралу з попереднім номером. Так — це табличний інтеграл (беремо одне з значень первісних):

. (3.21)

Користуючись (3.21), обчислимо за допомогою (3.20): , .

.

Для — :

=

,

і т.д. Таким чином можна обчислити інтеграл для будь-якого натурального показника .

Приклад 35. .

Для підінтегрального виразу є лише один спосіб розбиття його на частки і :

.

Часто при обчисленні інтегралу треба користуватися декількома методами, наприклад, методом інтегрування за частинами і методом заміни змінної. Наступні приклади ілюструють такі варіанти.

Приклад 36. .

Застосуємо до цього інтегралу формулу інтегрування за частинами, маючи для підінтегрального виразу лише один можливий спосіб розбиття на частки і :

.

Для обчислення інтегралу в правій частині останньої рівності скористуємося методом заміни змінної:

.

Остаточно отримуємо:

.

Приклад 37. .