
- •Міністерство освіти і науки україни одеський національний політехнічний університет методичні вказівки
- •Невизначений інтеграл і методи його обчислення
- •Первісна і невизначений інтеграл
- •Властивості невизначеного інтеграла
- •Таблиця основних невизначених інтегралів (тоні)
- •3. Найпростіші правила інтегрування
- •4. Інтегрування раціональних функцій
- •Розкладання правильних раціональних функцій на найпростіші
- •Інтеграли, які містять квадратний трьохчлен
- •Інтегрування деяких ірраціональних функцій
- •Інтегрування тригонометричних функцій
- •Різні приклади
Міністерство освіти і науки україни одеський національний політехнічний університет методичні вказівки
ДО ПРАКТИЧНИХ ЗАНЯТЬ
ЗА КУРСОМ «МАТЕМАТИЧНИЙ АНАЛІЗ»
Невизначений інтеграл і методи його обчислення
Одеса ОНПУ 2009
МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
ОДЕСЬКИЙ НАЦІОНАЛЬНИЙ ПОЛІТЕХНІЧНИЙ УНІВЕРСИТЕТ
Затверджено
на засіданні кафедри ІММЗІС
протокол № 3 від 20 жовтня 2009 р.
МЕТОДИЧНІ ВКАЗІВКИ
ДО ПРАКТИЧНИХ ЗАНЯТЬ ЗА КУРСОМ «МАТЕМАТИЧНИЙ АНАЛІЗ»
для студентів спеціальностей 6.040302 — Інформатика, 6.040301 — Прикладна математика
НЕВИЗНАЧЕНИЙ ІНТЕГРАЛ І МЕТОДИ ЙОГО ОБЧИСЛЕННЯ
Одеса ОНПУ 2009
Методичні вказівки до практичних занять за курсом «Математичний аналіз» для студентів спеціальностей 6.040302 — Інформатика, 6.040301 — Прикладна математика. Невизначений інтеграл і методи його обчислення / Укл. А.А. Кобозєва. — Одеса: ОНПУ, 2009. — 85 с.
Укладач: А.А. Кобозєва,
д.т.н.,доцент
Первісна і невизначений інтеграл
У багатьох питаннях науки й техніки виникає необхідність відновлювати функцію по її відомій похідній.
Будемо
говорити, що функція
![]() в
інтервалі
в
інтервалі
![]() називається
первісною
функцією
для функції
називається
первісною
функцією
для функції
![]() ,
якщо
,
якщо
![]() .
(1.1)
.
(1.1)
Нехай
![]() — первісна для
— первісна для
![]() ,
тоді будь-яка
,
тоді будь-яка
![]() ,
де
,
де
![]() ,
також буде первісною для
,
також буде первісною для
![]() .
Дійсно,
.
Дійсно,
![]() .
.
Таким чином, якщо функція має первісну, то вона має безліч первісних, до того ж всі ці первісні відрізняються лише на сталу.
Основна
теорема інтегрального числення.
Нехай функція
![]() визначена і неперервна
на
визначена і неперервна
на
![]() .
Тоді
.
Тоді
![]() має первісну на цьому інтервалі.
має первісну на цьому інтервалі.
Скрізь
далі довільну сталу будемо позначати
![]() .
.
Множина
усіх первісних для функції
![]() називається невизначеним
інтегралом
для
називається невизначеним
інтегралом
для
![]() і позначається
і позначається
![]() :
:
![]() ,
,
де
![]() —
одна з первісних функції
—
одна з первісних функції
![]() ,
,
![]() .
.
Властивості невизначеного інтеграла
Нехай
функції
![]() ,
,
![]() ,
,
![]() визначені на
визначені на
![]() ,
а
,
а
![]() ,
,
![]() ,
,
![]() — їх відповідні первісні на
— їх відповідні первісні на
![]() .
Через
.
Через
![]() будемо
позначати диференціали відповідних
функцій. Тоді
будемо
позначати диференціали відповідних
функцій. Тоді
 ;
;
 ;
;
 ,
де
,
де
 ;
;
 .
.
Таблиця основних невизначених інтегралів (тоні)
 ;
2.
;
2.
 ;
;
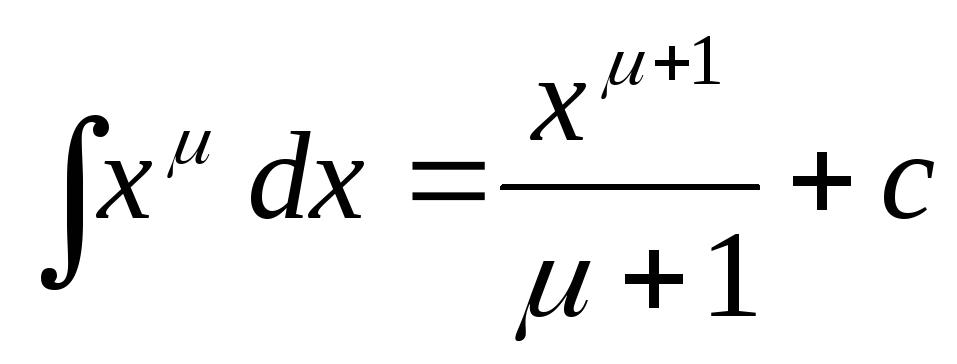 ,
де
,
де
 ;
4.
;
4.
 ;
;
 ;
6.
;
6.
 ;
;
 ;
8.
;
8.
 ;
;
9.![]() ;
10.
;
10.![]() ;
;
 ;
12.
;
12. ,
,
 ;
;
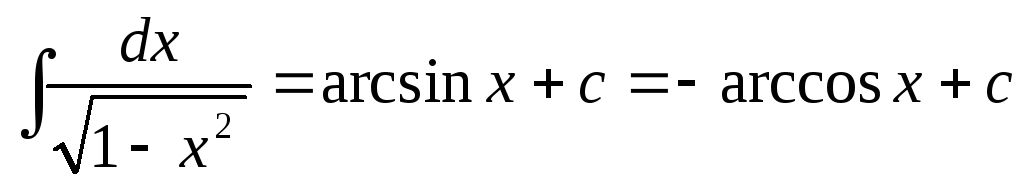 ;
14.
;
14. ,
,
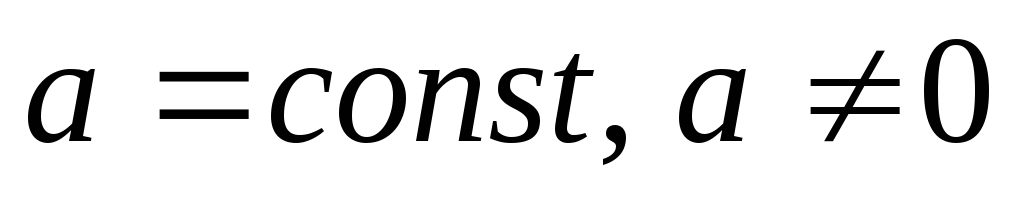 ;
;
 ;
;
 ,
,
 —
довгий логарифм;
—
довгий логарифм;
 ;
;
 —високий
логарифм.
—високий
логарифм.
При
обчисленні невизначеного інтеграла
легко перевіряється правильність
отриманого результата за допомогою
формули (1.1): похідна від знайденої
первісної
![]() повинна співпадати з поданою функцією
повинна співпадати з поданою функцією
![]() .
.
Перевіремо,
наприклад, правильність формули 18 в
ТОНІ. Для цього знайдемо похідну від
правої частини і порівняємо її з
підінтегральною функцією
![]() :
:
![]() .
.
При
користуванні ТОНІ треба бути уважними
при використанні формул 12, 14, 16, 18, де
присутній параметр
![]() .
Наприклад, інтеграл
.
Наприклад, інтеграл
![]() має вигляд 12 в ТОНІ, а стала 3 розглядається
як
має вигляд 12 в ТОНІ, а стала 3 розглядається
як
![]() ,
тому
,
тому
![]() ,
а
,
а
![]() .
.
