
- •Одесский национальный медицинский университет
- •Общие положения
- •Потенциал действия
- •Общие положения
- •Распространение потенциала действия Распространение потенциала действия по немиелинизированным волокнам
- •Распространение потенциала действия по миелинизированным волокнам
- •Активные свойства мембраны
- •Проводимость для калия gKна единицу площади [s/cm²]
- •Проводимость для натрия gNaна единицу площади [s/cm²]
- •Уравнение Нернста
- •Вывод уравнения Нернста
- •Литература
- •Дополнительная литература
Активные свойства мембраны
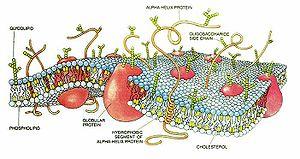
Схема строения мембраны клетки.
Активные свойства мембраны, обеспечивающие возникновение потенциала действия, основываются главным образом на поведении потенциалзависимых натриевых (Na+) и калиевых (K+) каналов. Начальная фаза ПД формируется входящим натриевым током, позже открываются калиевые каналы и выходящий K+-ток возвращает потенциал мембраны к исходному уровню. Исходную концентрацию ионов затем восстанавливаетнатрий-калиевый насос.
По ходу ПД каналы переходят из состояния в состояние: у Na+каналов основных состояний три — закрытое, открытое и инактивированное (в реальности дело сложнее, но этих трёх достаточно для описания), у K+каналов два — закрытое и открытое.
Поведение каналов, участвующих в формировании ПД, описывается через проводимость и высчиляется через коэффициенты переноса(трансфера).
Коэффициенты переноса были выведены Ходжкиными Хаксли.[1][2]
Проводимость для калия gKна единицу площади [s/cm²]
![]()
|
|
|
где: |
|
|
|
|
|
|
|
|
Проводимость для натрия gNaна единицу площади [s/cm²]
рассчитывается сложнее, поскольку, как
уже было сказано, у потенциал-зависимых
Na+ каналов, помимо закрытого/открытого
состояний, переход между которыми
описывается параметром
![]() ,
есть ещё инактивированное/не-инактивированное
состояния, переход между которыми
описывается через параметр
,
есть ещё инактивированное/не-инактивированное
состояния, переход между которыми
описывается через параметр![]()
![]()
|
|
|
|
где: |
где: |
|
|
|
|
|
|
|
|
|
|
|
|
Уравнение Нернста
Уравнение Нернста— уравнение связывающееокислительно-восстановительный потенциалсистемы сактивностямивеществ, входящих вэлектрохимическое уравнение, истандартными потенциаламиокислительно-восстановительных пар.
Вывод уравнения Нернста
![]() ,
,
где
![]() —универсальная
газовая постоянная, равная 8.31
Дж/(моль·K);
—универсальная
газовая постоянная, равная 8.31
Дж/(моль·K);
![]() —
абсолютная температура;
—
абсолютная температура;
![]() —число
Фарадея, равное 96485,35 Кл/моль;
—число
Фарадея, равное 96485,35 Кл/моль;
![]() —
числомолейэлектронов,
участвующих в процессе;
—
числомолейэлектронов,
участвующих в процессе;
![]() и
и![]() —активностисоответственноокисленнойивосстановленнойформ вещества, участвующего в полуреакции.
—активностисоответственноокисленнойивосстановленнойформ вещества, участвующего в полуреакции.
Если в формулу Нернста подставить числовые значения констант RиFи перейти отнатуральных логарифмовкдесятичным, то приT= 298K получим
![]()
Литература
Шахмаев Н.М., Шахмаев С.Н., Шодиев Д.Ш. Курс физики для средней школы. М., Просвещение, 1991.
Ландсберг Г. С. Элементарний учебник физики, М., Высшая школа, 1969.
Ремизов А.Н. Медицинская и биологическая физика, М., Высшая школа, 1982.
Савельев И.В. Курс общей физики. М., Наука, 1982.
Гольдфарб Н.И. Сборник вопросов и задач по физике. М., Высшая школа, 1975.
Тиманюк В.А. Фізіка, Харьков, Основа, 1996.с – 517с.
