
Учебное пособие по изучению модуля № 3 курса “Теор
.pdf
|
|
|
|
|
71 |
|
|
|
|
|
|
|
ε2 (t ) = [sˆ (t ) − s(t )]2 . |
(22.1) |
|||
Иначе говоря, критерием оптимальности фильтра является минимум среднего квадрата ошибки восстановления сигнала. В такой постановке задача была решена А.Н. Колмогоровым (1939 г.) для дискретных случайных последовательностей и Н. Винером (1941 г.) для непрерывных процессов. Поэтому оптимальный (в указанном смысле) линейный фильтр называется фильтром Кол- могорова-Винера.
Действующие на входе фильтра сигнал s(t) и помеха n(t) проходят через фильтр независимо и создают на выходе фильтра соответственно фильтрованные сигнал sвых(t) и помеху nвых(t). С учетом этого ошибка восстановления запишется
ε(t ) = sˆ (t ) − s(t ) = (sвых (t ) − s(t )) + nвых (t ) = s(t ) + nвых (t ). |
(22.2) |
Слагаемое s(t) отражает составляющую ошибки, обусловленную линейными искажениями полезного сигнала фильтром. Средний квадрат ошибки ε2 (t ) запишется
|
|
|
|
|
|
|
|
|
|
|
ε2 (t ) = s2 (t ) + n2 |
(t ). |
(22.3) |
||||||
|
|
|
|
|
вых |
|
|
|
|
|
|
|
|||||||
Величина линейных искажений полезного сигнала фильтром |
s2 (t ) зави- |
||||||||
сит от степени отличия АЧХ фильтра от постоянной величины и степени отли-
чия ФЧХ от линейной зависимости. Средний квадрат шума nвых2 (t ) на выходе фильтра зависит только от АЧХ фильтра. Для того чтобы линейные искажения полезного сигнала были минимальными, ФЧХ фильтра должна быть линейной
ϕ(ω) = – ωt0, |
(22.4) |
где t0 – задержка сигнала в фильтре. Понятно, что с учетом задержки соотно-
шение (22.1) имеет вид ε2 (t ) = [sˆ (t ) − s(t − t0 )]2 . Это уточнение не влияет на критерий оптимальности, поскольку в системах связи и вещания ожидаемая задержка сигнала в фильтре несущественная.
Перейдем к определению АЧХ фильтра. Для этого определим спектральные плотности мощностей левой и правой частей соотношения (22.2)
Gε (ω) = G s (ω) + Gn вых (ω). |
(22.5) |
||
Выразим СПМ помехи на выходе фильтра через СПМ помехи n(t) и ис- |
|||
комую АЧХ фильтра: |
|
|
|
Gn вых (ω) = Gn (ω)H 2 (ω). |
(22.6) |
||
По определению СГП ергодичного процесса |
|
||
G s (ω) = lim |
S 2s (ω) |
|
|
|
, |
(22.7) |
|
|
|||
T →∞ |
T |
|
|
где S s(ω) – амплитудный спектр ошибки за счет линейных искажений |
s(t); |
||
72 |
|
Т – длительность реализации Ds(t). |
|
Поскольку амплитудный спектр сигнала sвых(t) |
определяется как |
S(w)×H(w), где S(w) – амплитудный спектр сигнала s(t), то |
|
S s (ω) = S (ω)[H (ω) −1]. |
(22.8) |
Переходя от амплитудных спектров к СПМ, получим |
|
G s (ω) = Gs (ω)[H (ω) −1]2 . |
(22.9) |
После подстановки соотношений (22.6) и (22.9) в (22.5) получим |
|
Gε (ω) = Gs (ω)[H (ω) −1]2 + Gn (ω)H 2 (ω). |
(22.10) |
Средний квадрат ошибки восстановления (средняя мощность) вычисляется
∞
e2 (t ) = Pε = 1 ∫ Gε (w)dw. (22.11) p 0
Поскольку функция Gε(w) ³ 0 на всех частотах, то,
на всех частотах, достигнем минимума величины e2 (t ). определим из условия экстремума функции Gε(w):
dGε((ω)) = 0 ;
dH w
обеспечив min Gε(w)
Искомую АЧХ H(w)
(22.12)
dGε (w) |
= 2Gs |
(w)[H (w) -1]+ 2Gn (w)H (w) = 0 . |
(22.13) |
||
dH (w) |
|
||||
|
|
|
|||
После решения уравнения (22.13) получим выражение для АЧХ фильтра
Gs (ω) |
|
H (w) = Gs (w) + Gn (w) . |
(22.14) |
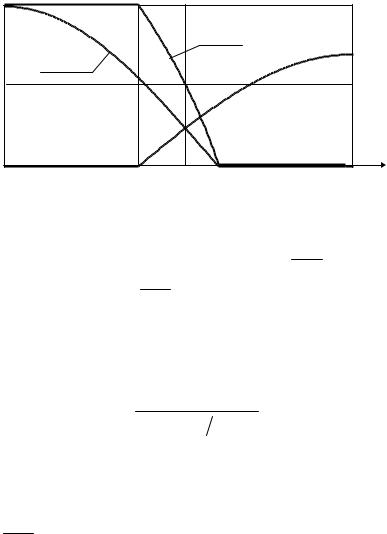
На рис. 22.1 иллюстрируется АЧХ ОЛФ, определенная соотношением
(22.14).
Из рис. 22.1 видно особенности АЧХ ОЛФ:
-на частотах, где Gn(f) = 0, значение АЧХ H(f) = 1 – в этих областях частот фильтр не должен вносить искажений;
-на частотах, где Gs(f) = 0, значение АЧХ H(f) = 0 – в этих областях частот фильтр должен полностью ослаблять составляющие помехи;
-на частотах, на которых Gs(f) = Gn(f), АЧХ H(f) = 0,5;
-на других частотах значения АЧХ определяются вычислениями по формуле (22.14).
Подставим выражение (22.14) в соотношение (22.10) для определения СПМ ошибки:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
73 |
|||
|
|
|
Gs (ω) |
|
|
|
Gs2 |
(ω) |
|
|
|
|
||||||||
|
|
Gε (ω) = Gs (ω) |
|
|
|
|
|
|
−1 |
+ Gn (ω) |
|
|
|
|
|
|
|
= |
|
|
|
|
|
(ω) + Gn (ω) |
[Gs |
(ω) + Gn |
2 |
||||||||||||||
|
|
Gs |
|
|
(ω)] |
|||||||||||||||
= |
Gs |
(ω)Gn2 (ω) + Gn (ω)Gs2 (ω) |
= |
Gs (ω)Gn |
(ω)[Gs (ω) + Gn (ω)] |
= |
Gs (ω)Gn (ω) (22.15) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
. |
|||||||||
|
[Gs (ω)+ Gn (ω)]2 |
|
|
|
|
[Gs |
(ω) + Gn (ω)]2 |
|
|
Gs (ω) + Gn (ω) |
||||||||||
1 |
|
|
H(f) |
Gn(f) |
|
Gs(f) |
||
|
||
0,5 |
|
|
0 |
f |
|
|
||
Рисунок 22.1 – Графическая иллюстрация АЧХ ОЛФ |
||
При подстановке соотношения (22.15) в выражение (22.11) можно вычис-
лить средний квадрат ошибки восстановления сигнала
Из (22.15) видно, что ошибка ε2 (t ) равна нулю только в том случае, когда Gs(f)Gn(f) = 0, т.е. когда спектры сигнала и помехи не перекрываются (хотя бы один с сомножителей равен нулю).
Перепишем соотношение (22.14) в виде
H (ω) = |
1 |
|
1 + Gn (ω) Gs (ω) . |
(22.16) |
Из последнего соотношения видно, что коэффициент передачи оптимального фильтра на каждой из частот тем меньше, чем больше отношение Gn(f)/Gs(f) на этой частоте.
Следует отметить, что оптимальные линейные фильтры, обеспечивающие минимум ошибки ε2 (t ), существенным образом отличаются от согласованных фильтров, рассмотренных ранее. Если основное назначение рассмотренных здесь фильтров состоит в наилучшем воспроизведении формы сигнала, то задача согласованных фильтров состоит в формировании максимального отношения сигнал/шум в момент отсчета.
При использовании ОЛФ в аналоговых системах связи и вещания выявляется такая особенность. Имеет место высокое отношение спектральных плотностей сигнала и шума: Gs(f)/Gn(f) >> 1. Выражение для АЧХ ОЛФ (22.14) в случае полосовых сигналов переходит в следующее
1, |
fmin ≤ |
f ≤ fmax |
, |
|
H ( f ) = |
f < fmin , |
f > |
|
(22.17) |
0, |
fmax, |
|||
где fmin и fmax – граничные частоты спектра сигнала. В случае НЧ сигналов

74
1, |
0 ≤ f ≤ F |
, |
|
|
|
max |
|
H ( f ) = |
0, |
f > F |
(22.18) |
|
|
max, |
|
где Fmax – максимальная частота спектра сигнала.
Таким образом, оптимальные линейные фильтры в системах связи и вещания имеют П-образную АЧХ.
Контрольные вопросы
1.Сформулируйте критерий оптимальности ОЛФ.
2.При каком условии ошибку восстановления сигнала можно свести к
нулю?
3.Объясните отличие ОЛФ и согласованного фильтра с точки зрения ослабления помех.
23.СРАВНЕНИЕ ПОМЕХОУСТОЙЧИВОСТИ ОПТИМАЛЬНЫХ ДЕМОДУЛЯТОРОВ СИГНАЛОВ АНАЛОГОВЫХ ВИДОВ МОДУЛЯЦИИ
Мы выяснили, что в условиях слабых помех демодулятор должен содержать: фильтр додетекторной обработки, детектор, фильтр последетекторной обработки. Для того, чтобы демодулятор был оптимальным, фильтры должны быть оптимальными. В условиях слабой помехи АЧХ фильтров должны быть П-образными:
–фильтр додетекторной обработки – полосовой фильтр, граничные частоты полосы пропускания которого совпадают с граничными частотами спектра модулированного сигнала;
–фильтр последетекторной обработки – ФНЧ, частота среза которого совпадает с максимальной частотой спектра первичного сигнала Fmax.
Помехоустойчивость определим в условиях действия АБГШ. Анализ помехоустойчивости состоит в определении выигрыша демодулятора в отношении сигнал/шум
g = |
Pb Pε |
. |
(23.1) |
|
Ps  Pn
Pn
Для определения выигрыша нужно определить 4 величины: Pb, Pε, Ps, Pn.
Оптимальный демодулятор сигнала балансовой модуляции. Матема-
тически сигнал БМ записывается
sБМ(t) = A0b(t)cos2πf0t. |
(23.2) |
Полосовой фильтр имеет полосу пропускания |
FБМ = 2Fmax. Для детекти- |
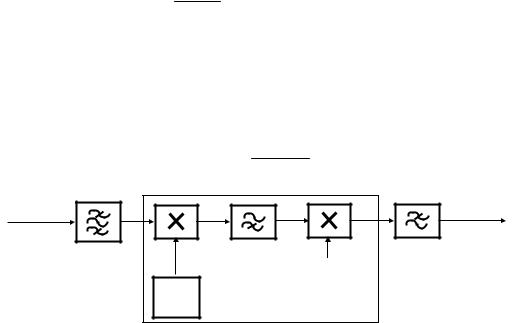
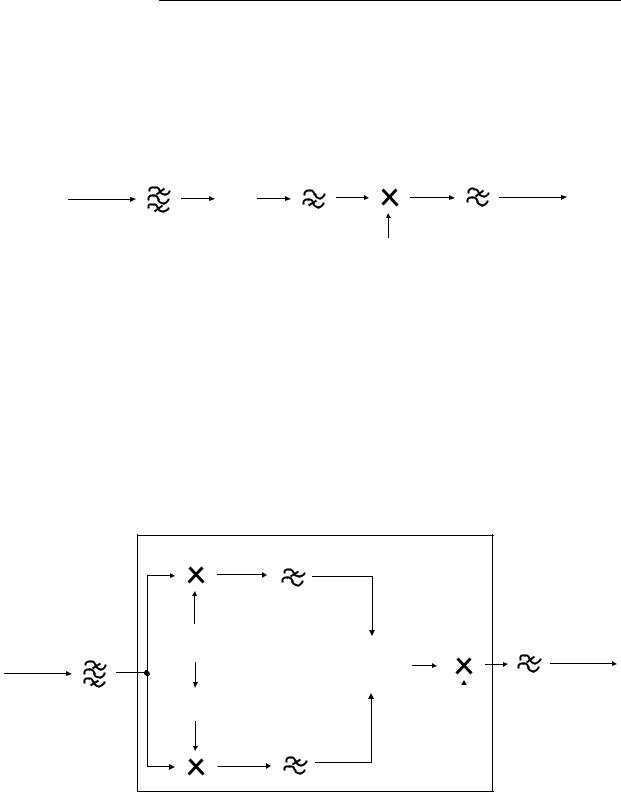
рования БМ сигнала необходимо использовать синхронный детектор (рис. 23.1). ФНЧ, являющийся обязательным элементом схемы синхронного детектора, используется как фильтр последетекторной обработки, т.е. частота среза фильтра равна Fmax, а АЧХ в полосе пропускания постоянная и равна 1.
Средняя мощность модулированного сигнала
P = s |
2 |
(t) = A2b2 |
(t) cos2 |
2πf |
0 |
t |
= 0,5 A2 |
P . |
(23.3) |
s |
БМ |
0 |
|
|
|
0 |
b |
|

75
Средняя мощность помехи на входе демодулятора Pn. На выходе перемножителя за счет сигнала имеем
A0b(t)cos2pf0t×2cos2pf0t = A0b(t) + A0b(t) cos2p2f0t. |
(23.4) |
s(t) + n(t) |
b(t) + e(t) |
2cos2pf0t 1/A0
G
СД
Рисунок 23.1 – Схема оптимального демодулятора сигналов БМ и ОМ
ФНЧ пропускает первый компонент, а второй ослабляет. С учетом умножения на 1/A0 на выходе демодулятора получим b(t). Его средняя мощность равняется Pb.
Помеху на входе синхронного детектора (как полосовой процесс) представим квадратурными составляющими
n(t) = NC(t)cos2pf0t + NS(t)sin2pf0t. |
(23.5) |
Мощность помехи делится поровну между квадратурными составляющими, мощность каждой из них Pn/2. Квадратурная составляющая помехи не проходит через синхронный детектор, и на выходе демодулятора получим
e(t) = NC(t)/A0. |
(23.6) |
Поскольку NC2 (t) cos2 2pf0t = Pn/2, а левая часть равенства равняется
0,5 NC2 (t) , то NC2 (t) = Pn, а
P = P / A2 . |
(23.7) |
||
ε |
n |
0 |
|
Определим выигрыш демодулятора
|
|
P × A2 |
× P |
|
|
|
|||
gБМ = |
|
|
b |
0 |
|
n |
|
= 2. |
(23.8) |
P |
|
× 0,5 |
× A2 |
× |
|
||||
|
|
P |
|
||||||
|
n |
|
|
0 |
|
b |
|
||
Оптимальный демодулятор сигнала однополосной модуляции. Мате-
матически сигнал ОМ записывается
sОМ(t) = A0 b(t)cos2pf0t ± A0 b~(t) sin2pf0t. |
(23.9) |
Оптимальный демодулятор сигнала ОМ выполняется по схеме, приведенной на рис. 23.1. Полосовой фильтр имеет полосу пропускания DFОМ = Fmax.
Средняя мощность модулированного сигнала
P = s |
2 |
(t) = A2 P . |
(23.10) |
s |
ОМ |
0 b |
|
Средняя мощность помехи на входе синхронного детектора Pn.
76
Синхронный детектор не пропускает квадратурную составляющую сигнала ОМ, поэтому на основе анализа демодуляции сигнала БМ на выходе демодулятора сигнала ОМ получим сигнал b(t). Его средняя мощность равняется Pb. Прохождение помехи через синхронный детектор проанализирован выше и получено значение мощности помехи на выходе демодулятора (23.7).
Определим выигрыш демодулятора
|
P × A2 |
× P |
|
||
gОМ = |
b |
0 |
n |
= 1. |
(23.11) |
P × A2 |
|
||||
|
× P |
|
|||
|
n |
0 |
b |
|
|
Оптимальный демодулятор сигнала амплитудной модуляции на базе синхронного детектора. Математически сигнал АМ записывается
sАМ(t) = A0(1 + mАМ×b(t))cos2pf0t. |
(23.12) |
Схема демодулятора сигнала АМ приведена на рис. 11.5. Полосовой фильтр имеет полосу пропускания DFАМ = 2Fmax. Исходя из приведенного выше анализа, очевидно, что на выходе ФНЧ за счет сигнала получим A0 + A0mАМ×b(t). Фильтр верхних частот ослабляет постоянную составляющую A0 и пропускает вторую составляющую A0mАМ×b(t).
Средняя мощность модулированного сигнала
Ps = s |
2 |
(t) = 0,5 A2 |
(1 + mАМ Pb). |
(23.13) |
|
АМ |
0 |
|
|
Для дальнейшего анализа удобно учесть (см. модуль 1), что Pb = 1/ K A2 , где KA – коэффициент амплитуды сигнала b(t).
Прохождение шума через синхронный детектор проанализирован выше. Мощность шума на выходе демодулятора сигнала АМ
Pn |
|
. |
(23.14) |
Pε = |
A2 |
||
m2 |
|
|
|
AМ |
0 |
|
|
s(t) + n(t) |
|
b(t) + e(t) |
|
2cos2πf0t |
1/(mAMA0) |
|
|
|
|
||
G |
|
СД |
|
|
|
|
|
Рисунок 23.2 – Схема оптимального демодулятора сигнала АМ |
|
||
Определим выигрыш демодулятора
|
(СД) = |
|
1/ K |
2 |
× m |
2 |
A2 |
× P |
|
|
|
2m |
2 |
|
|
|
|||
g |
|
|
A |
|
|
АМ |
|
0 |
|
n |
|
= |
|
|
АМ |
|
. |
(23.15) |
|
|
× 0,5A2 |
|
|
|
2 |
|
|
2 ) |
|
|
|
|
|||||||
|
АМ |
P |
(1 |
+ m |
|
/ K |
|
m |
2 |
+ K |
2 |
|
|
||||||
|
|
|
|
|
|
||||||||||||||
|
|
n |
|
|
0 |
|
|
|
АМ |
|
A |
|
АМ |
|
A |
|
|||
Демодулятор сигнала амплитудной модуляции на базе детектора оги-
бающей. Схема такого демодулятора приведена на рис. 23.3. Она отличается от схемы демодулятора на рис. 23.2 типом амплитудного детектора – синхронный детектор заменен детектором огибающей с целью упрощения схемы демодуля-
77
тора. Выходной сигнал детектора огибающей пропорциональный огибающей входного сигнала 
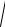 [A0 (1 + mAM b(t ))cos2πf0t + Nc (t )cos2πf0t]2 + [N s (t )sin2πf0t]2 .
[A0 (1 + mAM b(t ))cos2πf0t + Nc (t )cos2πf0t]2 + [N s (t )sin2πf0t]2 .
Поэтому помеху на выходе демодулятора создают как косинусная, так и синусная составляющие. Мощность помехи ε(t) будет вдвое большей, чем в случае синхронного детектора. Выигрыш демодулятора будет вдвое меньшим:
|
|
|
|
(ДО) |
= |
|
mАМ2 |
. |
|
(23.16) |
|||||
|
|
|
gAM |
|
|
|
|
||||||||
|
mАМ2 + KА2 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b(t) + ε(t) |
|
s(t) + n(t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ДО |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1/(mAMA0)
Рисунок 23.3 – Схема демодулятора сигнала АМ на базе детектора огибающей
Оптимальный демодулятор сигнала фазовой модуляции. Математи-
чески сигнал ФМ записывается
sФМ(t) = A0 cos(2πf0t + ∆ϕд·b(t)), |
(23.17) |
где ∆ϕд – девиация фазы сигнала, которую часто называют индексом фазовой модуляции mФМ.
Схема оптимального демодулятора сигнала ФМ приведена на рис. 23.4: ФНЧ1 и ФНЧ2 имеют частоты среза Fmax(mФМ + 1); ФНЧ3 – фильтр последетекторной обработки с частотой среза Fmax; АЧХ фильтров постоянная в полосах пропускания и равна 1; ФД – фазовый детектор.
|
|
|
|
|
|
|
|
|
ФНЧ1 |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
I(t) |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
2cos2πf0t |
|
|
|
|
|
|
|
|
|
|
|
|
ФНЧ3 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
Q(t ) |
|
|
|
|
|
|
b(t) + ε(t) |
|
|||
s(t) + n(t) |
|
|
|
|
|
|
|
|
|
arctg |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
I (t ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
π/2 |
πf0t |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
2sin2 |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
ФНЧ2 |
|
mФМ |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Q(t) |
|
ФД |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Рисунок 23.4 – Схема оптимального демодулятора сигнала ФМ |
||||||||||||||||||||||
Средняя мощность модулированного сигнала |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
= |
s 2 |
(t ) = 0,5A2 . |
(23.18) |
||||||||||||
|
|
|
|
|
|
|
s |
|
|
ФМ |
0 |
|
|
|
|
|
|
|
|
|
|||
Средняя мощность исходного сигнала Pb = 1/ K A2 .
78
Средняя мощность помехи на входе ФД Pn. Прохождение помехи через ФД анализируют при отсутствии модулирующего сигнала, т.е. b(t) ≡ 0, и s(t) = A0 cos2πf0t. Помеху представляют квадратурными составляющими в виде
(23.5). Тогда
I (t ) = (A0 + N c (t ))cos 2πf0t, |
Q(t ) = N s |
(t )sin 2πf0t, |
arctg |
Q(t ) |
= |
N s |
(t ) |
. (23.19) |
||||||
|
|
|
|
|
|
|||||||||
I (t ) |
|
A0 + Nc (t ) |
||||||||||||
|
|
|
|
|
|
|
|
|||||||
В условиях слабой |
помехи |
|Nc(t)| << A0, |
и помеха |
на |
выходе ФД |
|||||||||
Ns(t)/(A0mФМ), а ее мощность равна Pn/(A0mФМ)2. |
|
|
|
|
|
|
|
|
|
|
||||
Полоса пропускания ФНЧ3 в |
|
(mФМ +1)Fmax |
= m |
|
|
+1 раз меньше, чем |
||||||||
|
|
ФМ |
||||||||||||
|
|
|
Fmax |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
полоса пропускания ФНЧ2 и ширина спектра помехи Ns(t).
Поскольку спектр помехи равномерный, то мощность помехи ε(t) в mФМ + 1 раз меньше, чем мощность помехи Ns(t)/(A0mФМ) и определяется
|
|
|
Pε |
= |
|
Pn |
|
|
|
|
. |
|
(23.20) |
|
|
|
|
A2 m2 |
(m |
ФМ |
+1) |
|
|||||||
|
|
|
|
|
|
0 ФМ |
|
|
|
|
|
|
|
|
Определим выигрыш демодулятора |
|
|
|
|
|
|
|
|||||||
g |
|
= |
1/ K A2 × A0 |
2 mФМ2 (mФМ +1)Pn |
= |
mФМ2 |
2(m +1). |
(23.21) |
||||||
ФМ |
|
|
|
|||||||||||
|
|
Pn |
×0,5A0 2 |
|
|
|
|
|
K A2 |
ФМ |
|
|||
|
|
|
|
|
|
|
|
|
|
|||||
Оптимальный демодулятор сигнала частотной модуляции. Матема-
тически сигнал ЧМ записывается
SЧМ (t ) = A0 cos(2πf0t + 2π f д ∫ b(t )dt ), |
(23.22) |
где ∆fд – девиация частоты. Для последующего изложения удобно использовать
индекс ЧМ mЧМ = ∆fд/Fmax.
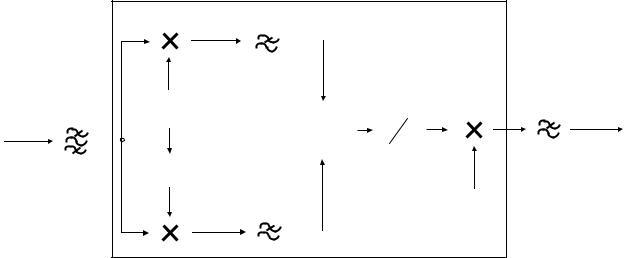
Схема оптимального демодулятора сигнала ЧМ приведена на рис. 23.5. Схема отличается от схемы демодулятора ФМ сигнала (рис. 23.4) наличием дифференциатора; ЧД – частотный детектор.
Средняя мощность модулированного сигнала
P = |
|
|
|
|
s 2 |
(t ) = 0,5A 2 . |
(23.23) |
||
s |
ЧМ |
0 |
|
|
Средняя мощность сигнала на выходе демодулятора Pb =1/ K A2 . Средняя мощность помехи на входе ЧД Pn.
Прохождение помехи через ЧД аналогично прохождению помехи через ФД, следует рассмотреть прохождение помехи Ns(t)/(A02π∆fд) через дифференциатор. Поскольку помеха Ns(t) – квазибелый шум в полосе частот Fmax(mЧМ + 1), то спектральная плотность мощности этой помехи на входе дифференциатора
79
Pn |
, 0 |
£ f £ Fmax (mЧМ |
+ 1). |
|
Fmax (mЧМ + 1) (A0 2pDfд )2 |
||||
|
|
|
Поскольку передаточная функция дифференциатора jω, то спектральная плотность мощности помехи на выходе дифференциатора
|
|
|
|
|
|
|
|
|
|
Pn (2πf )2 |
|
|
|
|
, |
0 ≤ f ≤ Fmax (mЧМ + 1). |
|
|
(23.24) |
||||||||||||||||||||||||||||
|
|
|
|
|
Fmax (mЧМ + 1) (A0 2π |
|
|
fд )2 |
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ФНЧ1 |
I(t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2cos2πf0t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q(t ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b(t)+ε(t) |
|||||||
s(t)+n(t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
arctg I (t ) |
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π/2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
2sin2πf0t |
|
ФНЧ2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2π f д |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q(t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЧД |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
Рисунок 23.5 – Схема оптимального демодулятора сигнала ЧМ |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
Определим мощность помехи e(t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
Fmax |
|
|
|
Pn |
|
f |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Pn |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
Pn |
||||||||||
Pε = |
∫0 |
|
|
|
|
|
|
|
|
|
df = |
|
|
|
|
|
|
|
× Fmax |
|
|
|
|
|
|
= |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
||||||||||||||||
Fmax (mЧМ +1) (A0 Dfд )2 |
3Fmax (mЧМ +1) A0 |
2 Dfд2 |
3А0 |
2 mЧМ2 (mЧМ +1) |
|||||||||||||||||||||||||||||||||||||||||||
|
Определим выигрыш демодулятора |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
gЧМ |
= |
1/ K A2 ×3A0 |
2 mЧМ2 |
(mЧМ +1)Pn |
= |
3mЧМ2 |
2(mЧМ +1). |
(23.25) |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Р ×0,5A 2 |
|
|
|
|
|
|
|
|
K |
A |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
При анализе мы выявили, что спектральная плотность мощности помехи |
||||||||||||||||||||||||||||||||||||||||||||||
e(t) имеет параболическую зависимость – |
формула (23.24): |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
G (f) = kf 2, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(23.26) |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ε |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где k – коэффициент пропорциональности. Эта особенность спектра часто учи-
тывается при разработке систем передачи с ЧМ.
Сравнение аналоговых систем передачи. Основными параметрами, по которым сравниваются системы передачи, является выигрыш демодулятора в отношении сигнал/шум g и коэффициент расширения полосы частот при модуляции a = ∆Fs/Fmax. Для рассмотренных методов модуляции эти параметры сведены в табл. 23.1.
Проведем сравнение числовых значений параметров при некоторых исходных данных: KА = 5; mЧМ = mФМ = 6; mАМ = 1.
80
Вычисления дают: gАМ = 0,038; gБМ = 2; gОМ = 1; gЧМ = 60,5; gФМ = 20,2.
Сравнение числовых значений выигрыша показывает, что самая низкая помехоустойчивость присуща системе передачи с АМ: выигрыш gАМ << 1, что логически назвать проигрышем. Однако АМ используется в системах радиовещания, где этот недостаток компенсируется простотой демодулятора на основе детектора огибающей (огромное количество более простых радиоприемников и один радиопередатчик с большей мощностью, чем при использовании БМ и ОМ).
Наибольшая помехоустойчивость присуща системе передачи с ЧМ. «Платой» за высокую помехоустойчивость является широкая полоса частот сигнала. Так, при Fmax = 3,4 кГц ∆FЧМ = 47,6 кГц, в то время как полоса частот сигнала ОМ ∆FОМ = 3,4 кГц.
Таблица 23.1 – Основные параметры аналоговых систем передачи
Метод модуляции |
|
g |
|
|
|
a |
Примечания |
||||||
|
|
|
|
|
2mАМ2 |
|
|
|
2 |
Синхронный |
|||
|
|
|
mАМ2 + K A2 |
|
детектор |
||||||||
|
|
|
|
|
|||||||||
АМ |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
mАМ2 |
|
|
|
2 |
Детектор |
||||||
|
|
|
|
|
|
|
|
||||||
|
2 |
|
|
|
2 |
|
огибающей |
||||||
|
|
|
|
|
|
||||||||
|
|
mАМ + KA |
|
|
|
||||||||
БМ |
|
2 |
|
|
|
|
|
2 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||
ОМ |
|
1 |
|
|
|
|
|
1 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
3m2 |
×a |
|
|
|
|||||
ЧМ |
|
|
|
ЧМ |
|
|
2(mЧМ + 1) |
rвх > rпр |
|||||
|
K A2 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
m |
2 |
×a |
|
|
|
|||
ФМ |
|
|
ФМ |
|
2(mФМ + 1) |
rвх > rпр |
|||||||
|
|
||||||||||||
|
|
|
|
|
K A2 |
|
|
|
|
|
|||
Порог помехоустойчивости демодулятора сигнала ЧМ. Из соотноше-
ния для выигрыша демодулятора ЧМ (23.25) вытекает, что, чем больше индекс mЧМ, тем больше выигрыш (правда, ценой увеличения полосы частот сигнала). Может показаться, что это дает возможность работать демодулятору со слабым сигналом (низким отношением сигнал/шум). Но, когда отношение сигнал/шум на входе демодулятора ρвх меньше порогового отношения сигнал/шум ρпр, то выигрыш демодулятора резко уменьшается (рис. 23.6). Такое явление резкого уменьшения величины выигрыша называют порогом помехоустойчивости приема сигнала ЧМ.
Пороговое отношение сигнал/шум ρпр несколько зависит от значения mЧМ (рис. 23.6). Считают, что демодулятор по схеме стандартного частотного детектора характеризуется ориентировочным значением ρпр = 10. Область значений ρвх, когда ρвх < ρпр, – это нерабочая область.
Были предложены так называемые порогопонижающие схемы демодуляторов сигналов ЧМ, которые получили названия:
