
Учебное пособие по изучению модуля № 3 курса “Теор
.pdf
31
рис. 10.1, но отличается опорными колебаниями в синхронных детекторах
(рис. 10.3).
|
|
as |
|
as |
s2 |
as |
s0 |
|
|
Обл. s2 |
|
Обл. s0 |
|
|
Обл. s3 |
|
aс |
ac |
ac |
|
Обл. s1 |
|
||
|
|
|
||
|
|
|
|
|
s3 |
|
s1 |
|
|
|
a |
б |
|
в |
Рисунок 10.2 – Разбивка пространства канальных символов на области сигналов:
а – ФМ-4; б – ФМ-8; в – КАМ-16
|
|
|
Перемно- |
|
Фильтр, со- |
|
Дискрети- |
|||||||
|
|
|
|
гласованный |
|
|||||||||
|
|
|
житель |
|
|
затор |
||||||||
|
|
|
|
с А(t) |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
cos (2π( f0 + |
|
2))t |
|
|
||
z(t) |
|
|
|
|
|
2 |
f |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
ТС |
|
|
|
|
ВН |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos (2π( f0 − |
|
2))t |
|
|
|||
|
|
|
|
|
|
2 |
f |
|
|
|||||
|
|
|
Перемно- |
|
Фильтр, со- |
|
Дискрети- |
|||||||
|
|
|
|
гласованный |
|
|||||||||
|
|
|
житель |
|
|
затор |
||||||||
|
|
|
|
с А(t) |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
aˆ1
Схема
решения
aˆ 0
Рисунок 10.3 – Оптимальный демодулятор сигнала ЧМ-2
ˆ (t) b
аˆ 0 Обл. s0
а 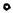
Обл. s1
а аˆ1
Рисунок 10.4 – Разбивка пространства сигналов ЧМ-2 на области сигналов
На рис. 10.4 показанная разбивка пространства канальных символов ЧМ-2 на области сигна-
лов. Граница областей показана жирной линией. Из этого рисунка видно, что для вынесения решения о переданном сигнале достаточно сравнить оценки амплитуд сигналов s0(t) и s1(t): если aˆ1 > aˆ 0 , то выносится решение sˆ1 и наоборот.
Контрольные вопросы
1.Объясните назначение отдельных блоков оптимального демодулятора двумерных сигналов КАМ-M и ФМ-М.
2.Сформулируйте правило вынесения решения на основе разбивки пространства канальных символов на М областей.

32
11. ВЕРОЯТНОСТЬ ОШИБКИ ПРИ ОПТИМАЛЬНОЙ ДЕМОДУЛЯЦИИ ОДНОМЕРНЫХ СИГНАЛОВ ЦИФРОВОЙ МОДУЛЯЦИИ
Как отмечалось в разд. 2, критерием оптимальности демодулятора является минимум полной вероятности ошибки решения относительно канального символа Рош. Но для пользователей количественной мерой помехоустойчивости
цифровой системы передачи является вероятность ошибки бита р. В двоичных системах передачи вероятности Рош и р совпадают. В случае многоуровневых видов модуляции сначала находят Рош, затем рассчитывают р, зная модуляционный код.
В.А. Котельников ввел термин «потенциальная помехоустойчивость приема» – это максимальная помехоустойчивость, которую обеспечивает оптимальный демодулятор. В сущности, это помехоустойчивость используемого модулированного сигнала при заданных характеристиках канала связи.
Анализ вероятности ошибки начнем из рассмотрения одномерных двоичных сигналов. Воспользуемся результатами, полученными в разд. 2. На рис. 2.1, б для одномерного двоичного сигнала показаны сигнальное созвездие и условные плотности вероятности оценки aˆ . Было сформулировано правило выне-
сения решения по результатам сравнения оценки аˆ с граничным значением λ:
если |
ˆ |
ˆ |
|
а > λ, то передавался символ s1(t), а если а< λ, то передавался символ |
|||
s0(t). Оптимальное значение λ находится посредине между а1 и а0: |
|
||
|
λ = 0,5(а1 + а0). |
|
(11.1) |
|
При этом вероятности ошибок при передаче сигналов s0(t) и s1(t) одинако- |
||
вы и определяются выражением |
|
|
|
|
Рош (s0 ) = Рош (s1 ) = ∞∫ p(aˆ s0 )daˆ = p . |
(11.2) |
|
|
λ |
|
|
|
Условная плотность вероятности p(aˆ s0 ) |
имеет нормальное распределе- |
|
ние вероятностей со средним значением, равным a0. С учетом этого (11.2) запишется
|
(s |
|
) = |
∞ |
p(aˆ s |
|
)daˆ |
|
λ − a0 |
|
|
|
|
Р |
0 |
∫ |
0 |
= Q |
|
, |
(11.3) |
||||||
|
|||||||||||||
ош |
|
|
|
|
|
σζ |
|
|
|
||||
|
|
|
|
λ |
|
|
|
|
|
|
|
где σζ – СКО шума на выходе согласованного фильтра, определенное раньше соотношением (5.14).
Примем к рассмотрению расстояние между сигналами
d = (а1 – а0). |
(11.4) |
Из соотношений (11.1) и (11.4) получим |
|
λ = а0 + 0,5d |
(11.5) |
С учетом (5.14) и (11.5) соотношение (11.3) дает вероятность ошибки ка-
нального символа в двоичной системе передачи

|
|
|
|
|
|
|
|
|
33 |
|
|
|
d |
|
|
|
|
|
|||
Р (2) = Q |
|
. |
|
|
|
(11.6) |
||||
|
|
|
|
|
||||||
ош |
|
2N0 |
|
|
|
|
|
|||
|
|
|
|
|
|
|||||
|
|
|
|
|
||||||
Из определения гауссовой Q-функции Q(z) = |
|
1 |
|
∞ |
−t2 2 dt следует, что, |
|||||
|
|
∫ e |
||||||||
|
|
|
||||||||
2π |
||||||||||
|
|
|
|
|
|
|
z |
|
||
|
|
|
|
|
|
|
|
|
||
чем большее значение аргумента, тем меньшее значение функции Q(z). Веро-
ятность ошибки канального символа (11.6) будет уменьшаться при увеличении расстояния между сигналами d и уменьшении удельной мощности шума N0 на входе демодулятора.
Дальше задача заключается в том, чтобы выразить расстояние между сигналами в (11.6) через физические параметры сигнала, действующего на входе демодулятора. Такими параметрами являются: средняя мощность модулированного сигнала Ps и скорость цифрового сигнала R или обратная к ней величи-
на – длительность двоичного символа Тб = 1/R.
Упражнение 11.1. Найдем вероятность ошибки для одномерных двоичных сигналов ФМ-2 и АИМ-2. На рис. 11.1 приведены созвездия сигналов ФМ-2 и АИМ-2. Поскольку базисная функция нормирована, то выполняется
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
равенство (5.12), и Еб = а2. Отсюда d = 2а = 2 Eб . |
||||||||||||
|
|
|
d |
|
|
|
||||||||||||||
|
|
|
|
|
|
|||||||||||||||
– а |
|
|
|
|
|
|
Вероятность ошибки бита определяется |
|
|
|
||||||||||
0 |
|
а |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
pФМ-2 = рАИМ-2 = Q( |
|
|
hб ), |
|
|||||||
Рисунок 11.1 – |
Сигнальное |
|
|
2 |
(11.7) |
|||||||||||||||
созвездие ФМ-2 и АИМ-2 |
где h2 |
= |
Eб |
– отношение сигнал/шум. |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
б |
|
N0 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Упражнение 11.2. Найдем вероятность ошибки для двоичного сигнала |
|||||||||||||||||||
АМ-2. На рис. 11.2 приведено созвездие сигнала АМ-2. |
Поскольку базисная |
|||||||||||||||||||
|
|
|
|
|
|
|
|
функция нормирована, то выполняется равенство |
||||||||||||
|
|
|
d |
|
|
|
||||||||||||||
|
|
|
|
|
|
(5.12), и Е1 = а2, а Е0 = 0. Еб = 0,5(Е1 + Е0) = 0,5а2. |
||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||
0 |
|
|
|
|
а |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
Отсюда d = а = 2Eб . |
|
|
|
|
|
|
||||||||||
Рисунок 11.2 – |
Сигнальное |
|
|
|
|
|
|
|||||||||||||
Вероятность ошибки бита определяется |
||||||||||||||||||||
|
|
созвездие АМ-2 |
||||||||||||||||||
|
|
|
|
|
pAМ-2 = Q(hб ). |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(11.8) |
||||||
Перейдем к многопозиционным системам передачи, т.е. М > 2. Если ка-
нальные символы равновероятны, то вероятность ошибки канального символа определяется
|
|
1 |
M -1 M -1 |
(si , s j |
). |
|
|
Pош |
= |
∑ ∑ Pош |
(11.9) |
||||
|
|||||||
|
|
M i=0 j=0 |
|
|
|
||
|
|
|
j¹i |
|
|
|
|
где Pош(si, sj) – вероятность ошибки в двоичной системе, использующей сигналы si и sj, а ошибка состоит в вынесении решения о передаче sˆ j , если было пе-
редано si. Чтобы упростить расчеты, учитывают переходы лишь в ближайшие сигналы (это допустимо при высоких отношениях сигнал/шум, которые соответствуют вероятности ошибки Рош < 10–2 ). Переход от ошибки канального

34
символа Рош к ошибке двоичного символа р выполняется легко, если используется модуляционный код Грея:
p = Pош n, де n = log2 M . |
(11.10) |
Упражнение 11.3. Найдем вероятность ошибки для многопозиционных одномерных сигналов АМ-М и АИМ-М. На рис. 11.3 приведены созвездия сигналов АМ-4 и АИМ-4. Аналогично стро-
d |
|
d |
|
|
|
d |
|
|
|
|
ятся созвездия при М > 4. Задачу будем |
|||||||
|
|
|
|
|
|
|||||||||||||
–3 а |
– а 0 |
а |
3а |
решать для произвольного М (М – |
целая |
|||||||||||||
Рисунок 11.3 – |
Сигнальное |
|
|
|
степень числа 2). |
|
||||||||||||
созвездие AМ-4 и АИМ-4 |
|
|
|
|
Коэффициенты аі принимают зна- |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
чения ± a, ± 3a,..., ± (M − 1)a . Определим |
|||||||
среднюю энергию канального символа |
|
|
|
|
|
|
|
|
||||||||||
|
|
Eсер = |
a2 + (3a)2 + ... + ((M -1)a)2 |
= |
(M 2 -1)2a2 |
. |
(11.11) |
|||||||||||
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
M 2 |
|
|
|
3 |
|
|
|||
Учтем, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
d = 2a и |
Eб = |
Eсер |
. |
(11.12) |
||||||||
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
log2 M |
|
|||||
На основе (11.11) и (11.12) получим выражение для квадрата расстояния |
||||||||||||||||||
|
|
|
|
|
|
|
|
d 2 = |
6 × Eб × log2 M |
. |
(11.13) |
|||||||
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
M 2 -1 |
|
|
|
|
|
||
При анализе вероятности ошибки достаточно учесть переходы лишь в ближайшие канальные символы, поэтому
|
|
|
|
|
|
|
d |
|
|
|
|
|
|
|
|||
|
|
|
P |
= 2Q |
|
|
|
. |
|
|
|
|
(11.14) |
||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
ош |
|
|
2N0 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
Учитывая (11.10), (11.13) и (11.14) получим выражение вероятности |
|||||||||||||||||
ошибки двоичного символа |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
2 |
|
|
|
|
|
6 × log2 M |
|
|
||||
p |
AМ−M |
= р |
АИМ−M |
= |
|
|
|
Q |
|
|
|
|
|
|
|
× h . |
(11.15) |
|
|
|
|
|
|
|
2 |
|
|||||||||
|
|
|
log2 M |
|
|
|
|
|
M |
-1 |
|
б |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Контрольные вопросы
1.Запишите и объясните формулу вероятности ошибки канального символа в двоичной системе передачи.
2.Объясните, что представляет собой величина hб2 .
3.Объясните, какие упрощения допускают при анализе помехоустойчивости многопозиционных сигналов.

35
12. ВЕРОЯТНОСТЬ ОШИБКИ ПРИ ОПТИМАЛЬНОЙ ДЕМОДУЛЯЦИИ ДВУМЕРНЫХ СИГНАЛОВ ЦИФРОВОЙ МОДУЛЯЦИИ
При анализе помехоустойчивости двумерных сигналов может возникнуть одна из двух ситуаций.
1. Линия, которая соединяет сигналы si и sj, входящие в формулу (11.9), совпадает с одной из осей координат пространства сигналов. В этом случае вероятность ошибки в двоичной системе, использующей сигналы si и sj, определяется формулой (11.6), как и в случае одномерных сигналов.
2. Линия, которая соединяет сигналы si и sj, входящие в формулу (11.9), не совпадает ни с одной из осей координат пространства сигналов (рис. 12.1).
На этом рисунке |
показаны |
шумовые компоненты |
оценок: aˆ c = aci |
+ ζc |
и |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ˆ |
= asi + ζ s , где ζс и |
ζs |
– |
|
|
|
|
|
|
|
|
|
s |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
as |
гауссовские независимые |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
величины с нулевым средним и СКО σ = |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N0 2 |
– |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ζs |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
формула (5.14). На основе рис. 12.1 условие воз- |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
90°– α |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
α |
|
|
|
|
никновения ошибки – вынесение решения о пере- |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ˆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
si |
|
|
|
|
даче s j , если было передано si |
|
|
||||||||||||
|
|
|
|
|
|
|
ζc |
|
|
|
|
|
|
|
Pош(si, sj) = Р {η > d/2}, |
|
|
|||||||||||||||||
Рисунок 12.1 – |
Действие шу- |
|
(12.1) |
|||||||||||||||||||||||||||||||
|
мовых компонент оценок |
где η = ζс cos α +ζs |
cos (90°– α) гауссовская слу- |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
чайная величина. Ее дисперсия |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ση2 = ζc2 cos2 α + ζ 2s sin 2 α = σ2 = N0 2 . |
(12.2) |
||||||||||||
|
|
|
|
Таким образом, и в случае ситуации 2 вероятность ошибки (12.1) опреде- |
||||||||||||||||||||||||||||||
ляется формулой (11.6), как и в случае одномерных сигналов. |
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
Упражнение 12.1. Найдем вероятность ошибки для многопозиционного |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
двумерного сигнала ФМ-4 (рис. 12.2): координаты |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
as |
d |
|
|
|
|
|
|
|
канальных символов ±а, |
а расстояния между бли- |
||||||||||||
|
|
s2 |
|
|
|
|
|
|
|
|
|
|
|
s0 |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
жайшими символами d |
= |
2a. Энергии канальных |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
символов одинаковые |
E = 2a2 = d 2 2 . Энергия сиг- |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
нала на бит |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
a |
|
|
|
|
a |
|
aс |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
Eб = Е 2 = d 2 4; |
d = 2 |
|
. |
(12.3) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Eб |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s1 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
s3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Из рис. 12.2 видно, что достаточно учесть пе- |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
реходы лишь в два ближайших канальных символа, |
|||||||||
Рисунок 12.2 – |
Сигнальное |
|||||||||||||||||||||||||||||||||
поэтому, учитывая формулу (11.6) |
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
созвездие ФМ-4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
d |
|
|
|
|
P = 2Q |
|
|
. |
(12.4) |
||
|
|
|
||||
ош |
|
2N0 |
|
|
|
|
|
|
|
|
|||
|
|
|
||||
Учитывая формулы (11.10) и (12.4), получим выражение для вероятности ошибки двоичного символа при ФМ-4
pФМ−4 = Q( |
|
hб ). |
|
2 |
(12.5) |

36
Упражнение 12.2. Найдем вероятность ошибки для многопозиционного сигнала ФМ-М. Точки сигнального созвездия находятся на окружности радиуса
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sj |
|
|
|
|
|
|
|
|
|
|
|
а с угловым шагом 2p/М. Ясно, что доста- |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
точно учесть переходы лишь в два бли- |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
жайших канальных символа. На рис.12.3 |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а d/2 |
|
|
|
|
|
|
|
|
|
|
|
приведен |
фрагмент |
|
|
|
созвездия сигнала |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
si |
|
|
|
|
|
|
|
ФМ-М. Выразим расстояние между бли- |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
π/М |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
жайшими точками через радиус окружно- |
|||||||||||||||||||||||||||||||||
Рисунок 12.3 – |
Фрагмент сигнального |
сти. |
Поскольку |
|
|
|
|
d/2 = a×sin(p/M), то |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
созвездия ФМ-M |
|
|
|
|
|
d = 2a sin(p/M). |
|
Энергии канальных симво- |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
одинаковые: Е |
= |
|
|
|
а2. |
|
|||||||||||||||||||||||||||||||||||||||||||||||||
лов |
|
|
|
|
Энергия |
|
|
сигнала |
|
|
|
на |
|
бит |
определяется |
|||||||||||||||||||||||||||||||||||||||||||
Eб = |
|
|
E |
|
|
|
= |
|
|
a2 |
|
и расстояние d = 2sin |
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
Eб log2 M . |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
log2 M |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
log2 M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
Используя формулы (11.10) и (12.4), получим выражение для вероятности |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
ошибки двоичного символа при ФМ-М для М ³ 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
ФМ−М |
= |
|
|
|
|
Q sin |
|
|
|
|
2log |
2 |
M h |
. |
|
|
|
|
|
|
(12.5) |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
log2 M |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
|
б |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
Упражнение 12.3. Найдем вероятность ошибки для многопозиционных |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
двумерных сигналов КАМ-16 (рис. 12.4). |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
as |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Возьмем одну из четырех точек, которые раз- |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
3a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
мещены возле начала координат. Для любой |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
из них видно, что достаточно учесть переходы |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
лишь в четыре ближайших канальных симво- |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
–3 a |
|
|
|
|
– a |
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
3a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ac |
ла, поэтому, учитывая формулу (11.6) |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
– a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
|
|
= 4Q |
|
|
|
|
|
|
. |
|
(12.6) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ош |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
–3 a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2N0 |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
Рисунок 12.4 – Сигнальное |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
Найдем |
среднюю |
|
|
энергию |
канального |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
созвездие КАМ-16 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
символа |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Еср = (4×2а2 + 8×10а2 + 4×18а2)/16 = 10а2. |
|
|
|
|
|
|
(12.7) |
|||||||||||||||||||||||||||||||||
|
|
|
Энергия |
|
|
сигнала |
на |
|
бит |
определяется |
|
|
Eб |
= |
|
Eср |
|
= |
|
5a2 |
|
и |
расстояние |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
2 |
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
d = 2a = 
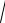 8Eб
8Eб 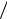 5 .
5 .
Используя формулы (11.10) и (12.6), получим выражение для вероятности ошибки двоичного символа при КАМ-16
pКАМ−16 = Q(0,89hб ). |
(12.8) |
Можно получить общую формулу вероятности ошибки бита для сигналов КАМ-М (М ³ 16) при условии, что log2M является четным числом

37
|
|
4 |
|
|
3log2 M |
|
pКАМ−М |
= |
|
|
|
|
|
|
|
|
||||
log2 M |
Q |
M -1 |
|
|||
|
|
|
|
|||
× hб . (12.9)
|
|
Упражнение 12.4. Найдем вероятность |
||
|
|
ошибки |
для |
двоичного сигнала ЧМ-2 |
|
(рис. 12.5): координаты канальных символов |
|||
а |
|
|||
|
d |
равны |
а, а |
расстояние между символами |
|
||||
d = 
 2 a. Энергии канальных символов одина-
2 a. Энергии канальных символов одина-
аковые E = a2 = d 2 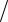 2 = Eб .
2 = Eб .
Рисунок 12.5 – |
Сигнальное |
|
|
По формуле (11.6) получим |
|
|
|
|||
|
|
PЧМ-2 |
= Q(hб ). |
|
(12.10) |
|||||
|
созвездие ЧМ-2 |
|
|
|
||||||
4 |
6 |
8 |
10 |
12 |
14 |
16 |
18 |
20 h2 |
, дБ |
|
|
|
|
|
|
|
|
|
б |
|
|
10– 3
10– 4
10– 5
10– 6
10– 7 |
|
10– 8 |
КАМ-64 |
|
|
р |
ФМ-16 |
|
|
10– 9 |
|
ФМ-2, |
АМ-2, ФМ-8 КАМ-16 КАМ-32 |
ФМ-4 |
ЧМ-2 |
Рисунок 12.6 – Помехоустойчивость оптимальных демодуляторов сигналов цифровой модуляции

38
Полученные в разд. 11 и 12 формулы позволяют определить вероятности ошибки бита р при заданном отношении сигнал/шум hб2 или необходимое отношение сигнал/шум при заданной вероятности ошибки бита. Анализ помехо-
устойчивости удобно проводить, используя графики зависимости р = f ( hб2 ) (рис. 12.6). При построении графика отношение сигнал/шум принято выражать в децибелах и использовать для него линейный масштаб. Для вероятности ошибки используют логарифмический масштаб.
Из приведенных на рис. 12.6 данных вытекает, что наивысшая помехоустойчивость свойственна сигналам ФМ-2 и ФМ-4.
Контрольные вопросы
1.Запишите и поясните формулы вероятности ошибки двоичного символа сигналов ФМ-4, ФМ-8, КАМ-16. Сравните помехоустойчивость.
2.Объясните, почему с ростом числа позиций сигнала ухудшается помехоустойчивость.
13.СИСТЕМЫ ВОССТАНОВЛЕНИЯ НЕСУЩЕГО КОЛЕБАНИЯ
Система восстановления несущего колебания (ВН) демодуляторов полосовых сигналов цифровой модуляции предназначена для формирования опорного гармонического колебания, фаза которого совпадает с фазой несущей, на основе которой сформирован демодулируемый сигнал.
Уже в 30-е годы прошлого столетия стало ясно, что сигналы ФМ-2 имеют наивысшую помехоустойчивость. Для применения этих сигналов в системах передачи необходимо было решить задачу восстановления несущего (опорного) колебания в демодуляторе, которое необходимое для работы синхронного де-
тектора. В те годы была предложена схема восстановления несущего колебания с умножением частоты на 2 (рис. 13.1).
z(t) |
|
R |
СФ |
uоп(t) |
|
|
b(t ) |
|
ˆ |
Дискр. |
CР |
х2 |
ВН
:2 |
ТС |
Рисунок 13.1 – Схема демодулятора сигнала ФМ-2 с восстановлением несущего колебания по методу умножения частоты на 2
В случае ФМ-2 si (t ) = ai A(t )cos2πf0t; i = 0, 1. Коэффициенты ai заданы созвездием сигнала (рис. 11.1). Канальные символы:
s1 (t ) = aA(t )cos2πf0t; s0 (t ) = aA(t )cos(2πf0t + π). |
(13.1) |
Много десятилетий использовались «слабо» фильтрованные импульсы A(t), которые были близки по форме к П-импульсу на интервале длительностью
Т

|
39 |
1, |
0 ≤ t ≤ T , |
A(t ) = |
(13.2) |
|
t < 0, t > T. |
0, |
После умножения частоты на 2, как сигнал s1(t), так и сигнал s0(t) дают a2cos2π2 f0t . Узкополосный фильтр имеет среднюю частоту полосы пропускания 2f0. Он предназначен для ослабления помех. Делитель частоты на 2 может выдать одно из двух возможных опорных колебаний:
−случай 1: uоп1 (t ) = cos2πf0t;
−случай 2: uоп2 (t ) = cos(2πf0t + π).
Оба колебания возможны, так как результат зависит от того, которые начальные условия сложатся в схеме делителя. Говорят, что опорное колебание имеет неопределенность фазы порядка 180°.
Вслучае 1 реализуется алгоритм оптимальной демодуляции сигнала ФМ-2. В случае 2 на выходе перемножителя, а затем и согласованного фильтра,
идискретизатора будут напряжения, противоположные тем, которые имеют место в случае 1. Схема решения будет выносить инверсные решения: вместо 1 выдает 0 и наоборот. Такое явление получило название инверсная (обратная) робота демодулятора. Оказалось, что и в процессе работы демодулятора могут происходить случайные скачкообразные переходы от колебания uоп1(t) к колебанию uоп2(t) и наоборот.
Вдемодуляторе сигнала ФМ-4 необходимо использовать умножитель частоты на 4, фильтр со средней частотой полосы пропускания 4f0 и делитель частоты на 4. После делителя частоты возникает одно из опорных колебаний,
которые отличаются по фазе с шагом 90°. Имеет место неопределенность фазы опорного колебания порядка 90°.
Устранить проявление неопределенности фазы опорного колебания в демодуляторе удается при использовании разностного (относительного) кодирования. Такие методы передачи получили название фазоразностной (относительной фазовой) модуляции.
Выше рассмотрена система ВН с возведением в степень. Однако она хорошо работает, когда амплитуда импульса A(t) близка к прямоугольной форме. Ныне используются импульсы Найквиста – импульсы с существенно сглаженной формой A(t). При такой форме импульса система ВН с возведением в степень работает плохо.
Опорное колебание необходимое для работы синхронного детектора (рис. 13.2). Пусть на вход детектора поступает сигнал ФМ-2. Канальный символ описывается
si (t ) = ai |
|
A(t )cos 2πf0t. |
|
2 |
(13.3) |
Если фаза колебания от генератора
uоп (t ) = |
|
cos(2πf0t + ϕ). |
|
2 |
(13.4) |

40
отличается от фазы несущей входного сигнала на величину Δϕ, то сигнал на выходе синхронного детектора получает множитель cosΔϕ:
uвых (t ) = ai A(t )cos ϕ . |
(13.5) |
Поскольку максимальное значение косинуса равняется единице и достигается лишь в случае Dj = 0, наличие разности фаз приводит к уменьшению уровня сигнала на выходе детектора. Если же Dj = p/2, то сигнал на выходе детектора вообще отсутствует: uвых (t ) ≡ 0 .
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ε |
|||
|
|
|
|
|
|
|
|
|
|
|
(t ) |
s(t) |
|
|
|
|
|||
s(t) |
|
|
|
|
|
|
|
|
|
uвых |
|
Детектор |
|||||||
|
R |
|
|
|
|
ФНЧ |
|
|
ошибки фазы |
|
|
uоп(t) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
uоп(t) |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
Г |
|
|
|
|
|
|
|
|
|
|
ГУН |
|
ФНЧ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 13.2 – Синхронный детектор |
|
Рисунок 13.3 – |
Схема ФАПЧ |
||||||||||||||||
Ныне система ВН – это система фазовой автоматической подстройки частоты (ФАПЧ) (рис. 13.3) со специальным детектором ошибки фазы, которая способна работать в условиях отсутствия несущей в спектре сигнала. Здесь ГУН – генератор, управляемый напряжением. При появлении напряжения ошибки фазы e, этим напряжением подстраивается частота и фаза колебания, производимого ГУНом, так, чтобы уменьшить величину ошибки фазы.
Рассмотрим построение детектора ошибки фазы в случае сигнала ФМ-2. Схема детектора содержит еще один дополнительный синхронный детектор,
опорным колебанием которого является 
 2 sin(2pf0t + Dj). Напомним, что работу синхронного детектора можно рассматривать как вычисление проекции s(t) на uоп(t). Два синхронных детектора отличаются опорными колебаниями, сдвинутыми по фазе на 90°. Поэтому получаемые напряжения с выходов синхронных детекторов являются квадратурными составляющими детектируемого сигнала.
2 sin(2pf0t + Dj). Напомним, что работу синхронного детектора можно рассматривать как вычисление проекции s(t) на uоп(t). Два синхронных детектора отличаются опорными колебаниями, сдвинутыми по фазе на 90°. Поэтому получаемые напряжения с выходов синхронных детекторов являются квадратурными составляющими детектируемого сигнала.
На рис. 13.4 показано созвездие демодулируемого сигнала ФМ-2 и вычисленные квадратурные составляющие в момент отсчета при условии, что демодулируется канальный символ с амплитудой а: I – синфазная составляющая, Q – квадратурная составляющая. На рис. 13.4, а ошибка фазы опорного колебания Dj = 0; при этом синхронные детекторы вычисляют I = а, Q = 0. На рис. 13.4, б ошибка фазы опорного колебания Dj > 0; при этом синхронные детекторы вычисляют I = а×cosDj, Q < 0. На рис. 13.4, в ошибка фазы опорного колебания Dj < 0; при этом синхронные детекторы вычисляют I = а×cosDj, Q > 0.
Видим, что знак значения Q соответствует ошибке фазы: а именно, если Q < 0, то Dj > 0 и необходимо уменьшать частоту и фазу ГУН, если же Q > 0, то Dj < 0 и необходимо увеличивать частоту и фазу ГУН. Таким образом, значение Q можно принять в качестве ошибки фазы e. Но ситуация со знаком Q противоположная при демодуляции канального символа с амплитудой – а.
