
Учебное пособие по изучению модуля № 3 курса “Теор
.pdf
|
11 |
Рош (s0 ) = ∞∫ p(aˆ s0 )daˆ . |
(2.14) |
λ |
|
Безусловная вероятность ошибки сигнала и бита |
|
p = P(s1 )Pош (s1 ) + P(s0 )Pош (s0 ) = 0,5[Pош (s1 ) + Pош (s0 )]. |
(2.15) |
Из рис. 2.1, а видно, что вероятности в квадратных скобках равные площадям заштрихованных областей. Легко видеть, что суммарная площадь будет минимальной, когда граница областей будет посредине между а1 и а0:
λ = 0,5(а1 + а0). |
(2.16) |
Такое значение λ показано на рис. 2.1, б. Видно, что |
при этом |
Рош(s1) = Рош(s0). Там же показана разбивка пространства сигналов (в этом при-
мере числовой |
оси) на области сигналов: |
область значений |
аˆ , |
где |
p(aˆ s1 ) > p(aˆ s0 ), |
является областью символа s1, |
а область значений |
аˆ , |
где |
p(aˆ 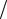 s1 ) < p(aˆ
s1 ) < p(aˆ 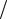 s0 ), является областью символа s0.
s0 ), является областью символа s0.
Примечание. Из рис. 2.1 видно, что вероятность ошибки зависит от значения СКО σ оценки аˆ – чем меньше СКО, тем меньшая вероятность ошибки. Ниже будет показано, что вычисление оценки по алгоритму (2.12) обеспечивает минимум значения СКО оценки.
Контрольные вопросы
1.Сформулируйте критерий оптимальности демодуляторов сигналов цифровой модуляции.
2.Сформулируйте правило решения по максимуму апостериорной вероят-
ности.
3.Сформулируйте правило решения по максимуму правдоподобия.
4.С какой целью проводят разбивку пространства сигналов на области сиг-
налов?
3.АЛГОРИТМ ОПТИМАЛЬНОЙ ДЕМОДУЛЯЦИИ СИГНАЛОВ ЦИФРОВОЙ МОДУЛЯЦИИ (ОБЩИЙ СЛУЧАЙ)
Полученное выше правило максимума правдоподобия отображено в виде
схемы оптимального демодулятора М-ичных сигналов (рис. 3.1). Отдельные блоки схемы выполняют следующие функции:
1.Определение координат сигнала z(t) в пространстве канальных символов на основе соотношения (2.7).
2.Определение квадратов расстояний между z(t) и si(t) в пространстве канальных символов на основе соотношения
d 2 (z, si ) = N∑−1(zk − aik )2 , i = 0, 1, …, M − 1. |
(3.1) |
k=0
3.Сравнение квадратов расстояний (или расстояний), определение номера j, которому отвечает минимальное значение d2(z, sj), выдача решения sˆ j .

12
4. Представление канального символа sj битами согласно модуляционному коду.
На следующем тактовом интервале перечисленные действия повторяют-
ся.
|
|
|
|
|
|
|
|
|
|
|
С х е м а р е ш е н и я |
|
|
|
|
|
|
||||||||
|
|
|
|
z0 |
|
|
|
|
|
|
d2(z, s0) |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Вычисления |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z1 |
|
|
Вычисления |
|
|
d2(z, s1) |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
координат |
|
|
|
|
|
|
|
|
Решение по |
|
|
|
|
Декодер |
|
|
||||||||
|
|
|
|
|
|
квадратов |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sˆ |
|
|
|
|
|||||
|
сигнала z(t) в |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ˆ |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
z(t) |
пространстве |
|
|
|
|
|
расстояний |
|
|
|
|
|
|
|
|
минимальному |
|
|
j |
|
модуляци- |
|
b(t ) |
||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
между |
|
|
|
|
|
|
|
значению |
|
|
|
|
|
онного |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
канальных |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
z(t) и si(t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
кода |
|
|
||
|
символов |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
zN–1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
d2(z, sM–1 ) |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 3.1 – Оптимальный демодулятор М-позиционного сигнала
Схема оптимального демодулятора (рис. 3.1) может использоваться для демодуляции сигнала произвольного заданного вида модуляции – виды модуляции отличаются значениями N и М, формой канальных символов. Ограничение одно – канальные символы равновероятные, но это ограничение на практике обычно выполняется.
В зависимости от вида модуляции, благодаря учету свойств канальных символов, по-разному могут вычисляться координаты сигнала z(t) в пространстве канальных символов. Это разнообразит способы построения демодуляторов, чему будет посвящено значительное место в следующих разделах. Другие блоки демодулятора: вычисление квадратов расстояний между z(t) и si(t), решение по минимальному расстоянию, декодирование решения на основе модуляционного кода являются стандартными для демодулятора, и в дальнейшем будут объединены в один блок, называемый «схема решения».
Вычисление координат сигнала z(t) в пространстве канальных символов на основе соотношения (2.7) может быть выполнено схемами корреляторов (рис. 3.2). Схема коррелятора содержит генератор сигнала ψk(t) – точной копии k-й базисной функции канальных символов, умножитель и интегратор со сбросом – в момент окончания сигнала ψk(t) берется отсчет, а интегратор приводится в нулевое состояние, чтобы быть готовым к обработке следующего сигнала. Название «коррелятор» связано с тем, что схема вычисляет значение функции взаимной корреляции между сигналами z(t) и ψk(t).
|
|
|
|
|
Ts |
|
|
|
|
|
|
|
|
z(t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
∫Ts |
|
|
|
|
|
|
|
zk |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
0 |
y(t) |
|
|
|
|
y(Ts) |
|||
|
|
ψk(t) |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||
G
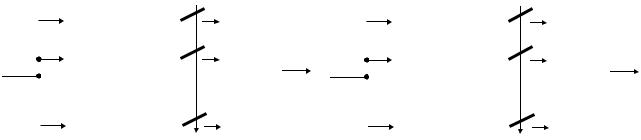
Рисунок 3.2 – Вычисление коэффициента zk коррелятором
Ts
z(t) СФ с  zk
zk
ψk(t)
Рисунок 3.3 – Вычисление коэффициента zk согласованным фильтром
13
Вычисление, которое соответствует соотношению (2.10), может быть выполнено линейной электрической цепью со специально подобранной импульсной реакцией gk(t). В общем случае выходной сигнал y(t) и входной сигнал z(t) линейной электрической цепи связаны соотношением, которое называется интегралом Дюамеля
y(t ) = ∞∫ z(τ)g(t − τ)dτ , |
(3.2) |
−∞ |
|
где g(t) – импульсная реакция цепи. |
|
Пусть |
|
gk(t) = ψk(Ts – t). |
(3.3) |
Поскольку сигнал ψk(t) существует на интервале (0, Ts), то на этом же интервале существует функция ψk(Ts – t). Поэтому границами интегрирования являются 0 и Ts. Будем искать значение уk(Ts)
yk (Ts ) = T∫s z(τ)ψk (Ts − Ts + τ)dτ = T∫s z(t )ψk (t )dt = zk . |
(3.4) |
|
0 |
0 |
|
Линейная электрическая цепь с импульсной реакцией (3.3) называется
фильтром, согласованным с сигналом ψk(t) (импульсная реакция является зер-
кальным отображением сигнала).
Таким образом, вычисление коэффициентов разложения сигнала z(t) может быть выполненное с помощью корреляторов или согласованных фильтров (рис. 3.3). Соответственно схема демодулятора будет содержать N корреляторов или N согласованных фильтров и схему решения (рис. 3.4).
|
|
|
|
|
|
Ts |
|
|
|
|
|
|
|
|
Ts |
|
|
|||
|
|
Коррел. ψ0(t) |
|
|
|
|
|
|
Схема |
|
|
СФ с ψ0(t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ˆ |
|
|
|
|
|
|
Схема |
ˆ |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
z(t) |
|
Коррел. ψ1(t) |
|
|
|
|
|
|
реше- |
b(t ) z(t) |
|
СФ с ψ1(t) |
|
|
|
|
|
реше- |
b(t ) |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
ния |
|
|
|
|
|
|
|
|
ния |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Коррел. ψN–1 (t) |
|
|
|
|
|
|
|
|
|
СФ с ψN–1 (t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
|
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 3.4 – Оптимальные демодуляторы: а – на основе корреляторов; б – на основе согласованных фильтров
Контрольные вопросы
1.Перечислите функции, которые выполняются отдельными блоками схемы оптимального демодулятора.
2.Как вычислить координаты сигнала z(t) в пространстве канальных симво-
лов?
3.По какому правилу работает схема решения оптимального демодулято-
ра?

14
4.СОГЛАСОВАННЫЙ ФИЛЬТР
Вразделе 3 введенное понятие «согласованный фильтр» (СФ) как устройство для вычисления коэффициента представления демодулируемого сигнала в ортонормированном базисе. СФ находит более широкое применение в аппаратуре систем передачи. Поэтому ниже рассматривается СФ из общих позиций.
Есть линейный четырехполюсник (фильтр) с передаточной функцией
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S( jω) = ∞∫ s(t )e− jωt dt – |
(4.1) |
|||||
|
|
|
|
|
|
|
− ∞ |
|
|
спектральная плотность сигнала s(t). Тогда спектральная плотность выходного сигнала ys(t) определяется
Sвых ( jω) = S ( jω)H ( jω). |
(4.2) |
Отсчетное значение сигнала ys(t0) определим как обратное преобразование Фурье от Sвых(jω) для момента времени t0
ys |
(t0 ) = |
1 |
∞ S ( jω)H ( jω)e jωt |
0 dω . |
(4.3) |
|
2π |
||||||
|
|
∫ |
|
|
||
|
|
|
− ∞ |
|
|
Мощность шума на выходе фильтра (средний квадрат отсчета шума yn(t0)) определяются
|
= |
|
|
|
|
|
1 |
∞ |
N0 |
|
H ( jω) |
|
2 dω. |
|
|
P |
y 2 |
(t |
|
) = |
(4.4) |
||||||||||
|
|
|
|
||||||||||||
0 |
2π −∞∫ 2 |
||||||||||||||
n вых |
|
n |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
15
Запишем отношение мгновенной мощности сигнала мощности шума Pn вых в отсчетный момент
|
|
1 |
2 |
∞ |
|
|
|
|
|
jωt |
2 |
|
||
|
|
|
|
|
∫ S( jw)H ( jw)e |
|
0 dw |
|
||||||
|
|
|
|
|||||||||||
r = |
|
2p |
− ∞ |
|
|
|
|
|
|
|
. |
|||
|
|
|
1 |
|
|
∞ |
|
|
||||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
× |
N0 |
∫ |
|
H ( jw) |
|
2 dw |
|
|||
|
|
|
|
|
|
|
||||||||
|
|
|
|
2p |
|
|
||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||
|
|
|
|
− ω |
|
|
|
|||||||
ys2(t0) к средней
(4.5)
Будем искать передаточную функцию H(jw), при которой имеет место максимальное значение числителя в соотношении (4.5). Воспользуемся тем, что
интеграл в |
числителе – скалярное произведение двух функций S*(jw) и |
H ( jw)e jωt0 |
(S*(jw) – функция, комплексно спряженная с функцией S(jw)). Ска- |
лярное произведение функций максимальное, если функции совпадают с точностью до произвольного положительного коэффициента c, т.е.
H ( jw)e jωt0 = с×S*(jw). Значит, максимум числителя (4.5) имеет место при передаточной функции
|
|
H ( jw) = с × S ( jw)e− jωt0 . |
|
|
(4.6) |
||||||||||||||||||||||
После подстановки выражения (4.6) в соотношение (4.5) получим |
|
||||||||||||||||||||||||||
|
|
1 2 |
|
2 ∞ |
|
S ( jw) |
|
|
2 |
|
|
2 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
с |
|
|
∫ |
|
|
|
|
dw |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
r = |
|
2p |
|
|
|
|
−∞ |
|
|
|
|
|
|
|
|
|
|
|
= |
2Es |
. |
(4.7) |
|||||
|
|
с2 |
|
|
N |
|
|
∞ |
S ( jw) |
|
2 |
|
|
|
|
N0 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
× |
0 |
|
∫ |
|
|
|
dw |
|
|
|
||||||||||||||
|
|
|
2p |
2 |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
−ω |
|
|
|
|
|
|
|
|
|
|||||||||||||
Здесь использовано, что энергия сигнала s(t) определяется |
|
||||||||||||||||||||||||||
|
|
|
Es |
= |
|
1 |
|
|
|
∞ |
|
S ( jω) |
|
2 dω. |
|
|
|
(4.8) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
2π |
|
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
− ∞ |
|
|
|
|
|
|
|
|
|
||||||
Видим, что при выполнении соотношения (4.6) обеспечивается не только максимум числителя отношения сигнал/шум (4.5), но и максимум этого отношения (значение ρ не зависит от конкретного вида передаточной функции H(jω), входящей в знаменатель). Таким образом, задача определения передаточной функции СФ H(jω) решена.
2. Соотношение (4.7) определяет максимально возможное отношение сигнал/шум на выходе фильтра в отсчетный момент. Это отношение принято называть пиковым
rпик |
= |
2Es |
. |
(4.9) |
|
||||
|
|
N0 |
|
|
Определим выигрыш в отношении сигнал/шум, показывающий во сколько раз увеличивается отношение сигнал/шум при фильтрации СФ,

16
|
g |
|
= |
ρпик |
= |
2Es |
× Pn |
= |
2PsTs N0 Fш |
= 2F T , |
(4.10) |
|
|
СФ |
|
|
|
|
|||||||
|
|
|
Ps Pn |
|
N0 |
× Ps |
|
|
ш |
s |
|
|
|
|
|
|
|
|
N0 × Ps |
|
|
||||
где Fш – |
шумовая полоса помехи на входе фильтра; |
|
|
|||||||||
Ts – |
длительность сигнала s(t); |
|
|
|
|
|
|
|||||
Ps и Pn – средние мощности сигнала и помехи на входе фильтра.
Из выражения (4.10) видно, что при определенных соотношениях между шумовой полосой помехи и длительностью сигнала выигрыш может принимать большие значения.
3. Найдем амплитудно-частотную и фазочастотную характеристики
СФ. Передаточная функция любой линейной электрической цепи определяет ее АЧХ и ФЧХ:
H(jw) = H(w) eхр(jj(w)), |
(4.11) |
где H(w) – АЧХ цепи, j(w) – ФЧХ цепи.
Представим спектральную плотность сигнала s(t) через модуль и аргу-
мент
S(jw) = S(w) exp(jy(w)), |
(4.12) |
где S(w) – амплитудный спектр сигнала, y(w) – фазовый спектр сигнала. |
|
После подстановки (4.11) и (4.12) в (4.6) получим, что АЧХ СФ |
|
H(w) = сS(w) |
(4.13) |
с точностью до произвольного коэффициента совпадает с амплитудным спектром сигнала, с которым фильтр согласован. Коэффициент передачи CФ больше на тех частотах, на которых больше составляющие сигнала s(t).
Равенство аргументов левой и правой частей (4.6) дает
j(w) = – y(w) – wt0, |
(4.14) |
что трактуется так: ФЧХ СФ с точностью до линейного слагаемого противоположна по знаку фазовому спектру сигнала, с которым фильтр согласован.
Для выяснения физической сущности ФЧХ СФ рассмотрим некоторую составляющую сигнала частоты fi: Aicos(2pfi t+ yi). Эта составляющая на выходе CФ определяется:
Ai(fi)cos(2pfit+ yi + j(fi)) = Ai(fi)cos(2pfit + yi – yi – 2 pfit0).
Полная фаза колебания равняется 2pfi(t – t0). В момент t = t0 полная фаза колебания равна нулю независимо от частоты. В этот момент все составляющие находятся в фазе и при сложении дают максимально возможное значение отклика.
4. Найдем импульсную реакцию СФ как обратное преобразование Фурье от передаточной функции
17
|
1 |
∞ |
c |
∞ |
|
|
g(t ) = |
∫ H ( jw)e jωt dt = |
∫ S (- jw)e |
− jωt0 e jωt dt = |
|||
|
|
|||||
|
2p −∞ |
2p −∞ |
(4.15) |
|||
= c ∞ ( w) jω(t −t ) = ( - ) p ∫ S j e 0 dt cs t0 t .
2 −∞
Видим, что импульсная реакция СФ является зеркальным отображением сигнала, с которым фильтр согласован, относительно точки t0 в масштабе с.
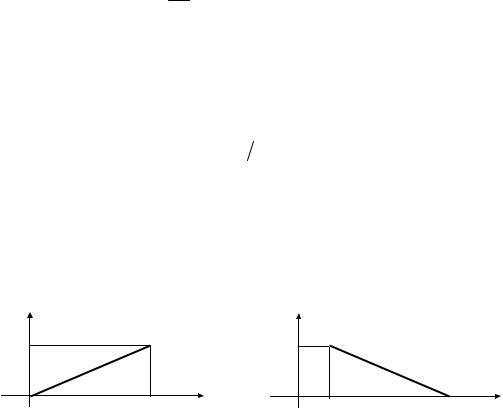
Пример 4.1. Построим график импульсной реакции фильтра, согласованного с сигналом
|
|
|
s |
|
s |
|
1 |
− t T , 0 |
≤ t ≤ T , |
||||
s(t ) = |
0, |
t < 0, |
t > T . |
|||
|
||||||
|
|
|
|
s |
||
Условием физической реализуемости линейной электрической цепи является требование к ее импульсной реакции: g(t) º 0 для значений t < 0. Из рис. 4.2 видно, что для выполнения этого условия необходимо наложить требование на момент отсчета: t0 ³ Ts, где Ts – длительность сигнала s(t).
s(t) |
|
g(t) |
||
|
|
|
|
|
|
1 |
|
|
c |
|
|
|
|
|
|
0 |
Ts |
t |
|
0 t0 – Ts |
t0 |
t |
а |
|
а |
|
|
|
б |
|
|
|
|
|
|
|
||
|
|
Рисунок 4.2 – |
Графики: а – сигнала; |
|
|
||
б– импульсной реакции фильтра, согласованного с сигналом
5.Пусть на входе СФ действует произвольный сигнал z(t). Отклик фильтра определяется интегралом Дюамеля
y(t ) = ∞∫ z(t)g(t - t)dt = c |
∞∫ z(t)s(t0 - t + t)dt = cK zs (t - t0 ), |
(4.16) |
−∞ |
−∞ |
|
где Kzs(t) – функция взаимной корреляции сигналов z(t) и s(t).
Из выражения (4.16) вытекает, что форма сигнала на выходе СФ определяется функцией взаимной корреляции входного сигнала и сигнала, с которым фильтр согласован, а именно, она повторяет функцию взаимной корреляции в масштабе с и смещена вправо на t0.
Если в соотношении (4.16) положить с = 1 и t0 = Ts, то легко убедиться, что y(Ts) дает значение скалярного произведения сигналов z(t) и s(t). Это свойство СФ использовалась выше для определения коэффициентов разложения – соотношение (3.4).
6. Пусть на вход СФ подается сигнал, с которым фильтр согласован. Тогда на основании (4.16) запишем
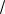
18 |
|
y(t ) = cK s (t − t0 ), |
(4.17) |
где Ks(t) – функция корреляции сигнала s(t).
Таким образом, если на вход СФ подается сигнал, с которым фильтр согласован, то отклик фильтра определяется функцией корреляции сигнала, а
именно, она повторяет функцию корреляции сигнала в масштабе с и смещена вправо на t0.
Упражнение 4.1. Проиллюстрируем рассмотренные свойства СФ на примере фильтра, согласованного с прямоугольным импульсом амплитуды А и длительности Ts. Пусть с = 1/A и t0 = Ts. Импульсная реакция фильтра, согласованного с П-импульсом, имеет П-образную форму, амплитуду 1 и длительность Ts, т.е. импульсная реакция совпадает с сигналом (рис. 4.3, а).
Спектральная плотность П-импульса определяется преобразованием Фу-
рье
Ts |
− jωt dt = |
A |
|
[e |
− jωTs -1]= |
2 A |
sin wTs × e− jωTs 2 . |
|
|
Sп(jw) = ∫ Ae |
(4.18) |
||||||||
- jw |
w |
||||||||
0 |
|
|
|
2 |
|
||||
На основе соотношения (4.6) получим выражение для передаточной функции фильтра, согласованного с П-импульсом, если с = 1/A и t0 = Ts
H(jw) = |
1 |
|
[1 - e− jωTs ] . |
(4.19) |
|
jw |
|||||
|
|
|
|||
Из этого соотношения вытекает, что схема фильтра, согласованного с П-импульсом, состоит из интегратора (с передаточной функцией 1/jw), устройства задержки на время Ts (с передаточной функцией exp(– jwTs)) и вычитателя (рис. 4.3, в). На этом рисунке цифрами обозначены отдельные точки схемы для обсуждения ее работы.
Легко получить выражение для АЧХ фильтра, согласованного с П-импульсом. Окончательное выражение для АЧХ после перехода к сменной f имеет вид функции sin(x)/x
H |
п |
( f ) = T |
|
sin πfTs |
|
. |
(4.20) |
|
|||||||
|
s |
|
|
|
|||
|
|
|
|
πfTs |
|
|
|
АЧХ СФ и амплитудный спектр сигнала показаны на рис 4.3, б.
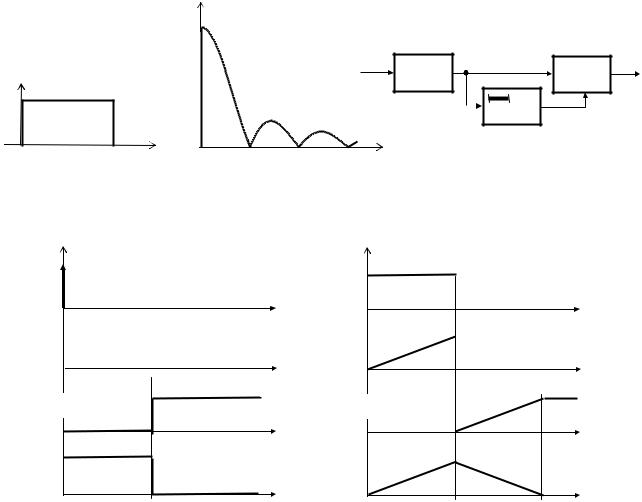
На рис. 4.4, а показаны процессы, имеющие место в СФ при подаче на его вход δ-функции. На выходе схемы наблюдается импульсная реакция. На рис. 4.4, б показаны процессы, имеющие место в СФ при подаче на его вход импульса, с которым фильтр согласован. На выходе схемы наблюдается отклик, совпадающий с корреляционной функцией П-импульса длительностью Тs (см. модуль 1).
19
|
Sп(f), Hп(f) |
|
|
|
|
|
|
1 |
∫ |
2 |
|
– |
4 |
s(t), g(t) |
|
|
||||
|
|
|
|
Ts |
3 |
|
|
|
|
|
|
|
0 |
|
|
|
Тs |
t |
0 |
1/Тs 2/Тs |
|
|
|
|
f |
|
в |
||
|
|
|
|
а |
|
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 4.3 – |
Характеристики фильтра, согласованного с П-импульсом: |
|||||||||||
|
|
|
|
|
а – |
импульсная реакция; б – |
АЧХ; в – |
схема фильтра |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
t |
3 |
|
|
3 |
|
|
|
|
|
t |
|
|
|
t |
4 |
|
|
4 |
|
|
|
0 |
Ts |
t |
0 |
Ts |
2Ts |
t |
|
а |
|
|
б |
|
|
Рисунок 4.4 – Временные диаграммы, иллюстрирующие работу фильтра, согласованного с П-импульсом
Контрольные вопросы
1.Что является критерием оптимальности согласованного фильтра?
2.Пересчитайте свойства согласованного фильтра.
3.Как определяется пиковое отношение сигнал/шум на выходе согласованного фильтра?
5.ПРИМЕНЕНИЕ СОГЛАСОВАННЫХ ФИЛЬТРОВ
ВДЕМОДУЛЯТОРАХ СИГНАЛОВ АИМ-М
Рассмотрим совместно схемы модулятора и демодулятора сигналов АИМ-М (рис. 5.1). Схема модулятора строится на основе описания канальных символов сигналов АИМ-М
si (t) = ai A(t), i = 0, 1, ..., M − 1, |
(5.1) |
где А(t) – импульс с определенными частотными и временными характеристиками;
ai – коэффициент, отображающий переданные биты.

20
На схеме КМК – кодер модуляционного кода, который вырабатывает коэффициенты ai на основе входного цифрового сигнала – на каждом тактовом интервале блока из n = log2M бит ставится в соответствие коэффициент ai. Этот коэффициент подается на вход формирующего фильтра (ФФ) сигналом aid(t). ФФ формирует импульс aiА(t).
Схема демодулятора построена на основе материала предыдущих разделов. На вход согласованного фильтра поступает сумма сигнала и помехи aiА(t) + n(t). Согласованный фильтр ослабляет помеху, и на его выходе имеет место полезный сигнал aiР(t) и помеха z(t). Дискретизатор берет отсчет и выдает оценку aˆ коэффициента ai. Максимальное значение импульса P(t) в момент отсчета равняется 1, поэтому aˆ = ai + z (оценку aˆ можно рассматривать как коэффициент z0 представления сигнала z(t) в одномерном пространстве относительно базисной функции А(t)). Дискретизатор управляется последовательностью импульсов от схемы тактовой синхронизации (ТС), что обеспечивает взятие отсчетов в моменты максимального отношения сигнал/шум. На основе полученной от дискретизатора оценки aˆ схема решения (СР) выносит решение о номере переданного канального символа и выдает решение двоичными символами согласно модуляционному коду.
|
|
|
aiδ(t) |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
aiP(t) + ζ(t) |
|
|
ˆ |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
aˆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
b(t) |
|
|
|
|
|
aiA(t) |
z(t) |
СФ с A(t) |
|
|
Дискр. |
|
|
|
b(t ) |
||||
|
КМК |
|
|
ФФ |
|
|
|
|
СР |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
ТС |
|
|
|
|
|
|||
|
|
|
|
|
|
|
б |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 5.1 – Схемы: а – модулятор сигналов АИМ-М; б – демодулятор сигналов АИМ-М
Поскольку формирующий фильтр возбуждается d-функцией, то амплитудный спектр импульса A(t) равняется АЧХ ФФ
SA(f) = HФФ(f). |
(5.2) |
Амплитудный спектр импульса Р(t) определяется |
|
SP(f) = SA(f)×HСФ(f), |
(5.3) |
где HСФ(f) – АЧХ фильтра, согласованного с импульсом A(t).
Импульс на выходе СФ Р(t) должен удовлетворять условию отсутствия межсимвольной интерференции (МСИ), поэтому потребуем, чтобы спектр SP(f) был спектром Найквиста N(f):
SP(f) = N(f). |
(5.4) |
Воспользуемся свойством СФ: его АЧХ совпадает с амплитудным спек- |
|
тром сигнала, с которым он согласован (при с = 1) |
|
HСФ(f) = SA(f). |
(5.5) |
Учитывая равенства (5.2)...(5.5) приходим к выводу, что |
|
