Контрольные вопросы

1. Что является количественной мерой помехоустойчивости цифровых систем передачи?

2. Что такое поэлементный прием цифровых сигналов?

3. Что является количественной мерой помехоустойчивости аналоговых систем передачи?

2. Критерий оптимальности демодуляторов сигналов цифровой модуляции и правила решения

Можно предложить огромное количество алгоритмов демодуляции сигнала (1.2). Каждый из алгоритмов демодуляции должен учитывать полностью или частично исходные данные: описание канальных символов s_i(t), i = 0, …, М – 1; априорные вероятности канальных символов Р(s_i), i = 0, …, М – 1; статистические характеристики помехи n(t), в частности, плотность вероятности р(n).

Наша задача – найти алгоритмы оптимальной демодуляции, считая, что критерием оптимальности является минимум полной вероятности ошибки решения демодулятора относительно канального символа. Для минимизации вероятности ошибки бита на выходе демодулятора при условии минимума вероятности ошибки решения относительно канального символа оптимизируют модуляционный код.

Очевидно, что минимум полной вероятности ошибки решения демодулятора относительно канального символа будет при вынесении решения по максимуму апостериорной вероятности канального символа . Правиломаксимума апостериорной вероятности формулируется так: демодулятор выносит решение о передаче символа , если выполняется система изМ – 1 неравенств:

. (2.1)

Дальше воспользуемся формулой Байеса

, (2.2)

где p(z) – безусловная плотность вероятности сигнала z(t);

p(z/s_i) – условная плотность вероятности сигнала z(t) при условии, что .

Здесь предполагается, что априорные вероятности канальных символов Р(s_i), i = 0, …, М – 1 и плотность вероятности помехи р(n) позволяют рассчитать условные плотности вероятности p(z/s_i). Обычно в системах передачи канальные символы равновероятные, т.е.

Р(s_i) = 1/М, i = 0, …, М – 1. (2.3)

С учетом этого перепишем систему неравенств (2.1), исключив из записи безусловную плотность вероятности p(z), входящую в правую и левую части и не зависящую от индекса:

. (2.4)

Система неравенств (2.4) выражает правило максимума правдоподобия, которое формулируется так: демодулятор выносит решение о передаче символа , если максимальна условная плотность вероятности сигналаz(t) при условии, что . Условные плотности вероятности называют такжефункциями правдоподобия.

Отметим, что правило максимума правдоподобия применяют для построения демодуляторов, если канальные символы равновероятные (в этом случае реализуется правило максимума апостериорной вероятности) или априорные вероятности канальных символов неизвестные.

Для перехода от правила решения (2.4) к алгоритму демодуляции следует воспользоваться представлением сигналов и помех в многомерном пространстве. Полным описанием множества канальных символов s_i(t), i = 0, …, М – 1 есть их представление в N-мерном пространстве (см. модуль 1). Там рассмотрены одномерные (N = 1) и двумерные (N = 2) сигналы, которые чаще всего используются. Для наглядности описания использовались сигнальные созвездия.

Реализация суммы сигнала и помехи z(t), которая подается на вход демодулятора, – соотношение (1.2) – также может быть представлена в многомерном пространстве, образованному базисными ортонормированными функциями _k(t), которые используются для описания и формирования канальных символов s_i(t):

(2.5)

, (2.6)

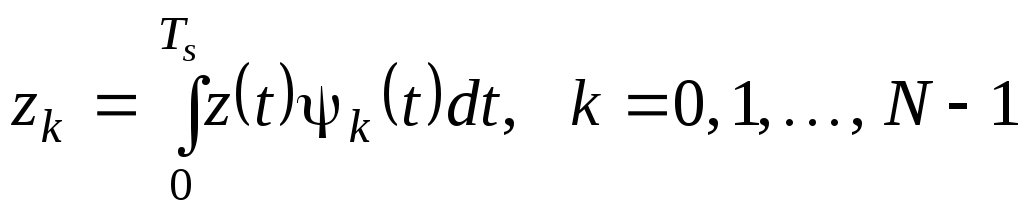, (2.7)

где z_k – коэффициенты разложения демодулируемого сигнала;

T_s – длительность канальных символов;

(0, T_s) – интервал ортогональности.

Коэффициенты z_k являются случайными гауссовскими некоррелированными величинами. Поэтому условные плотности вероятности p(z/s_i), i = 0, …, М – 1 имеют N-мерные распределения, которые определяются произведениями N одномерных распределений. Правая и левая части неровностей (2.4) перепишутся

(2.8)

где  – среднее квадратическое отклонение (СКО) коэффициентов z_k.

Проверке неравенств (2.8) эквивалентна проверка неравенств

. (2.9)

Суммы в соотношении (2.9) есть не что иное, как квадраты расстояний между демодулируемым сигналом и канальными символами в N-мерном пространстве. Последнее соотношение выражает правило максимума правдоподобия для оптимальной демодуляции: решение о номере канального символа выносится в пользу того сигнала, расстояние между которым и демодулируемым сигналом минимальное. Укажем, что нет необходимости извлечения корня квадратного из левой и правой частей неравенств (2.9), можно сравнивать и квадраты расстояний.

Правило работы демодулятораможно трактовать так:

• пространство сигналов разбивается на М непересекающихся областей с именами s_i, i = 0, …, М – 1; каждая область s_i – это совокупность точек, которые ближе к символу s_i(t), чем к другим символам;

• демодулятор выносит решение о передаче символа s_i(t), если точка z(t) в N-мерном пространстве попадает в область s_i.

Примечания. 1. Критерий минимума полной вероятности ошибки решения демодулятора в русскоязычной литературе называется также критерием идеального наблюдателя (термин введен В.А. Котельниковым).

2. Если ошибки решений демодулятора по-разному нежелательные для разных канальных символов, то используется критерий минимума среднего риска (критерий минимума полной вероятности ошибки решения демодулятора предполагает, что все ошибки одинаково нежелательны).

3. Если демодулятор решает задачу выявления сигнала известной формы (типичная задача в радиолокации), то используется критерий Неймана-Пирсона.

Пример 2.1. Найдем правило решения оптимальной демодуляции одномерного (N = 1) сигнала АИМ-2, у которого канальные символы описываются

, (2.10)

где А(t) – импульс с определенными временными и спектральными характеристиками, максимальное значение которого и энергия равны 1;

а_і – коэффициенты, которые отображают переданный бит: а₁ = а, а₀ = –а; число а определяет энергии канальных символов.

Функция А(t) играет роль базисной функции ₀(t) при представлении сигнала s_i(t) в одномерном пространстве.

На вход демодулятора на конкретном тактовом интервале (например, k = 0) поступает

. (2.11)

Найдем коэффициент представления сигнала z(t) в базисе А(t)

. (2.12)

где  – случайная величина с гауссовским распределением вероятностей, так как она является результатом линейного преобразования помехи с гауссовским распределением.

Согласно выражению (2.9) для восстановления двоичного символа, переданного на данном тактовом интервале, необходимо сравнить расстояния иz₀ ‑ a₀ и вынести решение в пользу меньшего из них: если , то, а еслиz₀ – a₁ > z₀ – a₀, то .

Из соотношения (2.12) видно, что z₀ есть не чем иным, как оценкой коэффициентаа_і. Обсудим правило вынесения решения на основе сравнения условных плотностей вероятностей (2.4) (правило максимального правдоподобия): демодулятор выносит решение о передаче канального символа , если>, и решение, если<.

На рис. 2.1 показано сигнальное созвездие АИМ-2 и условные плотности вероятности оценки коэффициента, описывающего демодулируемый сигнал. Из этого рисунка видно, что вместо сравнения условных плотностей вероятностей решение можно выносить по результату сравнения оценки с граничным значением по правилу: если >, то передавался символ s₁(t), а если <, то передавался символ s₀(t).

Вероятность ошибки при передаче s₁(t)

. (2.13)

Аналогично определяется вероятность ошибки при передаче s₀(t)

. (2.14)

Безусловная вероятность ошибки сигнала и бита

. (2.15)

Из рис. 2.1, а видно, что вероятности в квадратных скобках равныт площадям заштрихованных областей. Легко видеть, что суммарная площадь будет минимальной, когда граница областей будет посредине между а₁ и а₀:

 = 0,5(а₁ + а₀). (2.16)

Такое значение  показано на рис. 2.1, б. Видно, что при этом Р_ош(s₁) = Р_ош(s₀). Там же показана разбивка пространства сигналов (в этом примере числовой оси) на области сигналов: область значений , где>, является областью символаs₁, а область значений , где<, является областью символаs₀.

Примечание. Из рис. 2.1 видно, что вероятность ошибки зависит от значения СКО  оценки – чем меньше СКО, тем меньшая вероятность ошибки. Ниже будет показано, что вычисление оценки по алгоритму (2.12) обеспечивает минимум значения СКО оценки.