itirg_lr1

Міністерство освіти і науки, молоді та спорту України

ОДЕСЬКА НАЦІОНАЛЬНА АКАДЕМІЯ ХАРЧОВИХ ТЕХНОЛОГІЙ

Кафедра процесів, апаратів та енергетичного менеджменту

М Е Т О Д И Ч Н І В К А З І В К И

до лабораторних робіт з курсу

"Інформаційні технології в інженерних розрахунках галузі"

для студентів напряму підготовки 6.051701 денної та заочної форм навчання

Затверджено радою напряму підготовки бакалаврів

6.051701

Протокол № __ від ______________р.

Одеса ОНАХТ 2012

2

Методичні вказівки до лабораторних робіт з курсу "Інформаційні технології в інженерних розрахунках галузі" для студентів напряму підготовки 6.051701 денної та заочної форм навчання / Укладач О.В. Зиков, за ред. О.Г. Бурдо - Одеса:

ОНАХТ, 2012 - 30 с.

Укладач О.В. Зиков, канд.техн.наук.

За редакцією О.Г.Бурдо, д-ра техн.наук, професора.

Відповідальний за випуск зав. кафедрою процесів, апаратів та енергетичного менеджменту О.Г. Бурдо, д-р техн. наук, професор.

3

Зміст

1.Мета проведення лабораторних робіт

2.Лабораторна робота №1 Ознайомлення з пакетом «mathcad» та іншими прикладними програмами

a.Основні теоретичні положення

b.Визначення одиниць вимірювань

c.Проведення простих розрахунків на прикладі визначення середньої швидкості та еквівалентного діаметра.

i. Оформлення параметричної схеми і таблиці ідентифікації параметрів.

d.Представлення отриманих результатів у вигляді графічних залежностей.

e.Використання функцій та методів програмування в «mathcad» на прикладі розрахунку середньої різниці температур між рідкими теплоносіями.

f.Порядок проведення роботи.

g.Контрольні запитання.

3.Лабораторна робота № 2. Складання моделей теплофізичних властивостей харчових продуктів та теплоносіїв за експериментальними даними. Лінійна регрессія

a.Методи апроксимації табличних даних

b.Лінійна інтерполяція

c.Лінійна регресія.

d.Порядок проведення роботи.

e.Контрольні запитання.

4.Лабораторна робота № 3 Складання моделей теплофізичних властивостей харчових продуктів та теплоносіїв за експериментальними даними. Нелінійна регрессія

a.Сплайн-інтерполяція

b.Нелінійна регресія

c.Порядок проведення роботи.

d.Контрольні запитання.

5.Лабораторна робота № 4 Інженерний розрахунок рекуперативного теплообмінника (випарного апарата)

a.Основні теоретичні положення.

b.Порядок проведення роботи

c.Контрольні запитання

6.Лабораторна робота № 5 Розрахунок гідравлічного опору теплообмінника

a.Основні теоретичні положення.

b.Порядок проведення роботи.

c.Контрольні запитання.

7.Лабораторна робота № 6 Оптимізація конструктивних параметрів теплообмінника

a.Основні теоретичні положення.

b.Порядок проведення роботи.

c.Контрольні запитання.

8.Література

9.Додатки

a.Таблиці варіантів початкових даних

b.Таблиці теплофізичних властивостей

4

МЕТА проведення лабораторних робіт: закріпити теоретичний матеріал за відповідними темами курсу, що вивчається; ознайомити студентів з основами використання сучасних прикладних програм для інженерних розрахунків; набути навичок наукових досліджень і обробки даних з використанням ЕОМ; навчити студентів формулюванню робити логічних висновків за результатами отриманих даних.

В результаті проведення лабораторних занять студенти повинні:

ЗНАТИ: основні теоретичні положення дисципліни; принципи складання алгоритмів розрахунку інженерних задач; методи інженерних розрахунків на ЕОМ, основи рішення задач оптимізації з використанням ЕОМ.

ВМІТИ: реалізовувати алгоритми рішення інженерних задач на ЕОМ, проводити обробку експериментальних даних з використанням ЕОМ, виконувати за допомогою ЕОМ проектні та перевірочні розрахунки, а також проводити оптимізацію технологічних процесів і обладнання галузі.

5

Лабораторна робота №1

Ознайомлення з пакетом «mathcad» та іншими прикладними програмами

Мета роботи: ознайомитися з основними принципами виконання розрахунків в системі Матнсаd, визначити основні розмірності величин у вигляді, прийнятому в Україні, розробити математичну модель для розрахунку середньої швидкості потоку в трубах та еквівалентного діаметра міжтрубного простору кожухотрубного теплообмінника, провести розрахунки на моделі згідно заданому варіанту, результати представити у вигляді графіків.

Основні теоретичні положення

Математичний пакет Матнсаd призначений для роботи з документами. З погляду користувача, документ - це чистий лист паперу, на якому можна розміщувати блоки трьох основних типів: математичні вирази, текстові фрагменти і графічні області.

Розташування нетекстових блоків у документі має принципове значення - зліва направо і зверху вниз.

Математичні вирази.

До основних елементів математичних виразів Матнсаd відносяться типи даних,

оператори, функції і управляючі структури.

Оператори - елементи Матнсаd, за допомогою яких можна створювати математичні вирази. До них відносяться символи арифметичних операцій, знаки обчислення сум, добутків, похідної і інтеграла і так далі.

Оператор визначає:

-дія, яка повинна виконуватися за наявності тих або інших значень операндів;

-скільки, де і які операнди повинні бути введені в оператори.

Операнд - це число або вираз, на який діє оператор. Наприклад, у виразі 5! + 3 число 3 і вираз 5! - операнди оператора + (плюс), а число 5 операнд оператора факторіал (!). Після зазначення операндів оператори стають блоками, які виконуються по документу.

До типів даних відносяться числові константи, звичайні і системні змінні, масиви (вектори і матриці) і дані файлового типу.

Константами називають іменовані об'єкти, що мають деякі значення, які не можуть бути змінені. Змінні є іменованими об'єктами, що мають деяке значення, яке може змінюватися по ходу виконання програми. Тип змінної визначається її значенням; змінні можуть бути числовими, рядковими, символьними і так далі. Імена констант, змінних і інших об'єктів називають ідентифікаторами. Ідентифікатори в Матнсаd є набором латинських або грецьких букв і цифр.

У Матнсаd міститься невелика група особливих об'єктів, які не можна віднести ні до класу констант, ні до класу змінних, значення яких визначені відразу після запуску програми. Їх правильніше вважати системними змінними, що мають зумовлені системою початкові значення. Зміну значень системних змінних проводять у вкладці вбудованих змінних діалогового вікна Математика => Опції.

Звичайні змінні відрізняються від системних тим, що вони повинні бути заздалегідь визначені користувачем, тобто їм необхідно хоч б одного разу присвоїти значення. Як оператор присвоєння використовується знак :=, тоді як знак = відведений для виведення значення константи або змінної. Якщо змінній присвоюється початкове значення за допомогою оператора :=, яке викликається натисненням клавіші : (двокрапка) на клавіатурі, то таке присвоєння називається локальним. До цього присвоєння змінна не визначена і її не можна

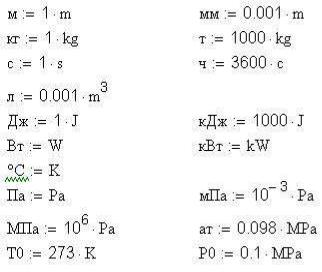
6

використовувати. Проте за допомогою знака. ≡ . (клавіша ~ на клавіатурі) можна забезпечити

глобальне присвоєння

Матнсаd прочитує весь документ двічі зліва направо і зверху вниз. При першому

проході виконуються всі дії, наказані глобальним оператором присвоєння ( . ≡ .), а при другому - проводяться дії, наказані локальним оператором присвоєння (:=). Всі необхідні результати обчислень відображаються за допомогою знака (=).

Існують також жирний знак рівності = (комбінація клавіш Ctrl + =), який використовується, наприклад, як оператор наближеної рівності при вирішенні систем рівнянь, і символьний знак рівності —> ( комбінація клавіш Сtr1 +.).

Дискретні аргументи - це особливий клас змінних, який в пакеті Матнсаd часто замінює структури, що управляють циклами (проте повноцінною така заміна не є). Ці змінні мають ряд фіксованих значень: цілочисельних (перший спосіб) або у вигляді чисел з певним кроком, змінних від початкового значення до кінцевого (другий спосіб).

оглавление

Порядок проведення роботи

а) визначення одиниць вимірювань

В MathCad вбудовано велику кількість одиниць виміру, за допомогою которих створюються розмірні змінні. При цьому можливо використовувати різні системи одиниць. Незручність для російськомовного користувача полягає в тому, в MathCad відсутні звичні позначення розмірностей, записані кирилицею, тому визначимо основні розмірності величин у вигляді, прийнятому в Україні, і збережемо їх у файлі DM.MCD. Текст цього документа наведено на рис. 1. Надалі будем використовувати ці дані, вставляючи в робочий документ посилання на файл DM.MCD.

Для того, щоб задати розмірність деякої змінної, досить значення цієї змінної помножити на позначення відповідної одиниці вимірювання.

Наприклад,

x := 1 × м

Позначення ° С найпростіше ввести, набравши на додатковому (цифровий) клавіатурі код 248, утримуючи клавішу Alt. Літера С в наших прикладах вводиться в латинскому регістрі.

Рисунок 1 - Визначення одиниць виміру

При обчисленнях MathCad виводить результат, використовуючи вбудовані одиниці вимірювання. Визначену користувачем одиницю виміру доводиться вводити вручну.

7

На початок

б) визначення середньої швидкості та еквівалентного діаметра

Для розробки математичної моделі необхідно визначити її вхідні і вихідні параметри. З мети роботи визничаємо, що вихідними параметрами моделі будуть середня швидкість потоку в трубах w, та еквівалентній діаметр міжтрубного простору de. Вхідними будуть усі параметри, що впливають на вихідні, а саме: об’ємна продуктивність G, діаметр труб d, діаметр кожуха D та кількість труб n. В результаті отримаємо параметричну схему, представлену на рис. 2.

Усі параметри, що використовуються в розрахунках, заносять до таблиці ідентифікації параметрів. При цьому потрібно пам’ятати, що позначення параметрів у формулах та в програмі не завжди збігаються.

Таблиця 1 - Таблиця ідентифікації параметрів

9

На початок

Використання функцій та методів програмування в маткаді на прикладі

розрахунку середньої різниці температур між рідкими теплоносіями

Напишемо функцію визначення середньої різниці температур між рідкими теплоносіями в залежності від їх початкових і кінцевих температур. При цьому потрібно враховувати, що якщо співвідношення між найбільшою і найменшою різницею температур між теплоносіями менше ніж 2, то середню різницю температур розраховуємо як середнє арифметичне між найбільшою і найменшою різницею температур, інакше як середнє логарифмічне. Якщо для розрахунку функції необхідно виконувати декілька дій, використовується оператор Add Line, який створює і при необхідності розширює жирну вертикальну лінію, праворуч від якої в шаблонах задається запис програмного блоку. Для розрахунків проміжних величин в середині програмного блоку (наприклад, більшої і меншої різниці температур) використовується оператор внутрішнього присвоювання ←. Щоб задати умови, при яких будуть проводитися розрахунки за заданою формулою, використовується оператор if. Якщо існує формула, за якою потрібно проводити розрахунки, коли не виконується ні одна умова із тих, що були задані після операторів if, то використовується оператор otherwise. Усі ці оператори знаходяться на панелі інструментів Programming.

Протокол роботи повинен містити в собі:

-Титульний аркуш.

-Мету роботи.

-Параметричну схему об’єкта.

-Таблицю ідентифікації параметрів.

-Графіки залежностей w=f(d), de=f(d).

Контрольні запитання:

1.Для чого призначений пакет MathCad?

2.Що таке оператори, операнди, функції?

3.Які типи даних використовуються в пакеті MathCad?

4.У якому порядку проводяться розрахунки в пакеті MathCad?

5.Як задати розмірність в пакеті MathCad?

6.Як записати послідовність чисел в пакеті MathCad?

На початок

10

Лабораторна робота № 2 Складання моделей теплофізичних властивостей харчових продуктів та

теплоносіїв за експериментальними даними. Лінійна регрессія

Мета роботи: ознайомитися з методами апроксимації табличних даних. Провести лінійну інтерполяцію теплофізичних властивостей продукту та теплоносія. Отримати регресійні рівняння залежностей теплофізичних властивостей від температури та знайти похибку отриманих залежностей.

Основні теоретичні положення

Методи апроксимації табличних даних

Нехай є таблична залежність однієї фізичної величини від іншої; наприклад, густини від температури. Позначимо табличні значення цих величин через Xi Yi. За цими даними потрібно побудувати деяку функцію y = f(x), що визначає безперервну залежність між цими величинами.

Один з методів побудови таких залежностей - інтерполяція, при якій функція f(x) будується таким чином, щоб в точках Xi виконувалася умова: Yi = f(Xi), а в проміжних точках функцію f(x) апроксимують поліномами. В MathCad реалізована: лінійна інтерполяція, при якій сусідні точки з'єднуються прямими линями (функція linterp); сплайн-інтерполяція, при якій сусідні точки з'єднуються відрізками кубічного полінома (функції cspline, pspline, lspline).

Другий метод апроксимації табличних даних - побудова функції регрессії, під якою розуміється функція відомого виду (наприклад, поліном) з коефіцієнтами підібраними таким чином, щоб f(x) наближала табличні дані найкращим чином. На відміну від функцій інтерполяції, ці функції не вимагають, щоб апроксимуюча крива проходила через точки даних.

Не існує однозначної відповіді на питання, який з методів апроксимації, інтерполяція або регресія, кращий. Кожен з методів має свої переваги і недоліки. Інтерполяція дуже чутлива до помилок даних, але не вимагає ніякої попередньої інформації про характер функціональної залежності. Функція регресії добре згладжує помилки табличних даних, однак вигляд цієї функції повинен бути заздалегідь відомий. При виборі способу апроксимації дуже допомагає аналіз графіків, на яких побудований графік функції f(x) і нанесені табличні точки (Xi, Yi).

На початок

Лінійна інтерполяція

Застосування лінійної інтерполяції дає хороші результати в наступних випадках:

1.Залежність між інтерпольованими даними близька до лінійної. Таку властивість має, наприклад, теплоємність газів.

2.Табличні дані представлені досить докладно.

3.Не потрібна висока точність наближення.

4.Отримана в результаті інтерполяції функція в подальшому не буде диференціюватися.

Наприклад, в розрахунках масообмінних процесів використовується похідна функції рівноваги. Рівноважні дані, як правило, отримані експериментально, причому з не дуже високою точністю. Процедура інтерполяції сама по собі чутлива до експериментальних похибок, а диференціювання інтерполяційної функції особливо відчутне. Але лінійна інтерполяція при диференренціюванні призводить до менших похибок.

Лінійна інтерполяція виконується функцією linterp, що має наступний формат: linterp(vx,vy,x), де vx, vy - вектори даних (однакової довжини), причому вектор vx повинен містити речові значення, розташовані в порядку зростання; x -аргумент, для якого функція interp повертає інтерпольовані значення.

Розглянемо застосування лінійної інтерполяції для залежності густини продукту від температури. Вектор Tabt містить значення температур, ° С; вектор Tabρ - значення густини, кг/м3 (рис. 4). Зауважимо, що обидва ці вектори повинні бути стовпцями, проте для компактності запису вони введені як рядки, до яких застосована операція транспонування. Оператор транспонування вводиться одночасним натисканням клавіш Ctrl+1.