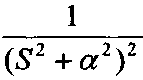- •2 Години| Лекція №4
- •Лекція №1
- •1. Підприємство сільськогосподарського машинобудування як об'єкт
- •2. Технологічний процес як основа автоматизації виробництва
- •Продуктивність автоматизованого| виробництва|. Надійність елементів| та автоматичних| систем.
- •1. Продуктивність автоматизованого виробництва.
- •2. Надійність елементів та автоматичних систем.
- •4 Години| Лекція 3
- •Основи класифікації ланок.
- •Основні поняття та визначення.
- •Лекція 3 Типові елементи (ланки) систем автоматичного керування.
- •2 Години Лекція 6 Регульовані об'єкти й автоматичні регулятори. Типи автоматичних систем. Вимоги, що ставляться до системи автоматичного регулювання.
- •3. Вимоги, що ставляться до системи автоматичного регулювання.
- •4 Години
- •6 Годин
- •Стійкість лінійних систем автоматичного регулювання.
- •1. Умови стійкості систем автоматичного регулювання.
- •3. Критерій стійкості Михайлова.
- •6. Визначення стійкості систем автоматичного регулювання.
- •4 Години
- •Функціональні, принципової і структурні схеми систем автоматики. Складання рівнянь динаміки систем.
- •1. Функціональні, принципової і структурні схеми систем автоматики
- •2. Система статичного регулювання.
- •3. Система астатичного регулювання.
- •Лекція 9 Отримання лінійних систем із заданими характеристиками
- •1. Показники якості систем автоматичного регулювання.
- •2. Коректуючі врмстроі
- •4 Години
- •3. Загальні відомості про циклове керування процесами.
- •4. Функції алгебри логіки та їх мінімізація.
2 Години| Лекція №4
Теорія|вживання| перетворення по Лапласу для аналітичного визначення рівнянь систем автоматичного керування.
Застосування|вживання| перетворення по Лапласу для вирішення диференціальних рівнянь руху систем автоматичного регулювання істотно|суттєвий| спрощує це завдання|задачу|, виключаючи необхідність визначення постійних інтеграцій. Це засновано на особливих властивостях Лапласовського зображення проведених|виробляти| функцій за різних початкових умов.
Процес автоматичного регулювання описується системою рівняння окремих ланок і рівняннями зв'язків між ними. Зазвичай|звично| систему розкладають на найбільш прості, елементарні ланки, порядок|лад| диференціальних рівнянь яких не перевищує два.
Хай|нехай| рівняння ланки буде:
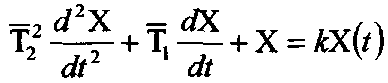
Введемо|запроваджуватимемо|
заміну![]() тоді
рівняння запишеться|занотовуватиме|
у вигляді|виді|;
тоді
рівняння запишеться|занотовуватиме|
у вигляді|виді|;
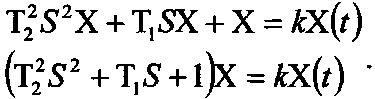
Якщо оригінал Х(t) є функцією змінної t, то зображення X(S) буде пов'язано з оригіналом залежністю;
![]()
![]()
На підставі прямого і зворотного перетворення Лапласа можна побудувати таблиці по перекладу оригіналів в зображення. Приведемо приклад для деяких функцій.
|
|
ОРИГІНАЛ
|
ЗОБРАЖЕННЯ
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При розрахунках систем автоматичного регулювання досить часто потрібно знати зображення функції для дії, що управляє або обурюючого|бентежити|.
Приклад|зразок| №1.
Виконати пряме перетворення Лапласа, для диференціального рівняння користуючись таблицею:
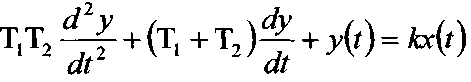
Використовуючи дані таблиці отримаємо|одержуватимемо|:
![]()
Приклад|зразок| №2.
Виконати зворотне перетворення по Лапласу для отримання|здобуття| рівняння з|із| оригіналами.
![]()
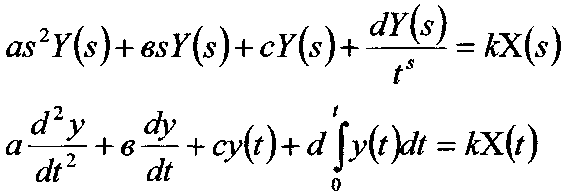
Приклад|зразок| №3.
Виконати пряме перетворення Лапласа для диференціального рівняння:

використовуючи таблицю отримаємо|одержуватимемо|:
![]()
У теорії автоматичного регулювання користуються не рівняннями об'єктів і пристроїв|устроїв| систем, записані через зображення функції, а їх передавальними функціями. Під передавальною функцією розуміють відношення|ставлення| зображення вихідний
величини для об'єкту або пристрою|устрою| системи до зображення функцій вхідної величини, отриманих|одержувати| за нульових початкових умов.
Використовуючи це визначення, знайдемо передавальні функції для прикладів|зразків| №1 і №2:
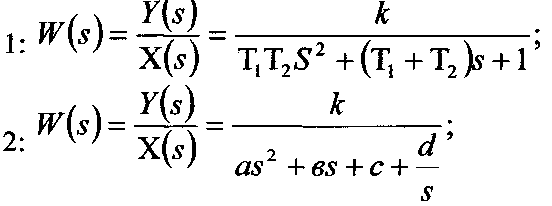
Визначити передавальну функцію сильфонного| датчика рідинного тиску|тиснення|; Рівняння роботи датчика
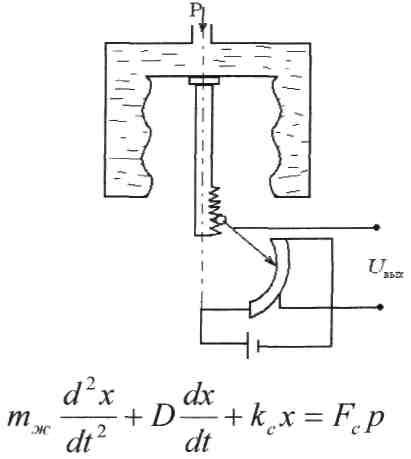
х-| переміщення рейки сильфона|; D-| коефіцієнт в'язкого тертя;
![]() коефіцієнт
пружності сильфона;
Fc-
площа сильфона.
Перетворимо рівняння;
коефіцієнт
пружності сильфона;
Fc-
площа сильфона.
Перетворимо рівняння;
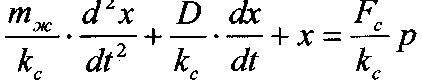
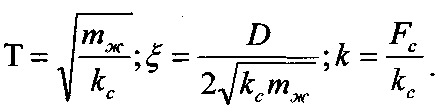
Отримаємо|одержуватимемо| рівняння після|потім| підстановки;

з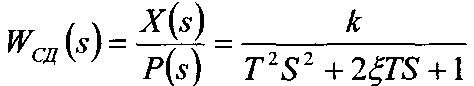 найдемо
передавальну функцію пристрою|устрою|
відношенням|ставленням|
вихідної величини до вхідної
найдемо
передавальну функцію пристрою|устрою|
відношенням|ставленням|
вихідної величини до вхідної
типовими, або стандартними. Найчастіше використовують ступінчасте, лінійне, синусоїдальне діяння.
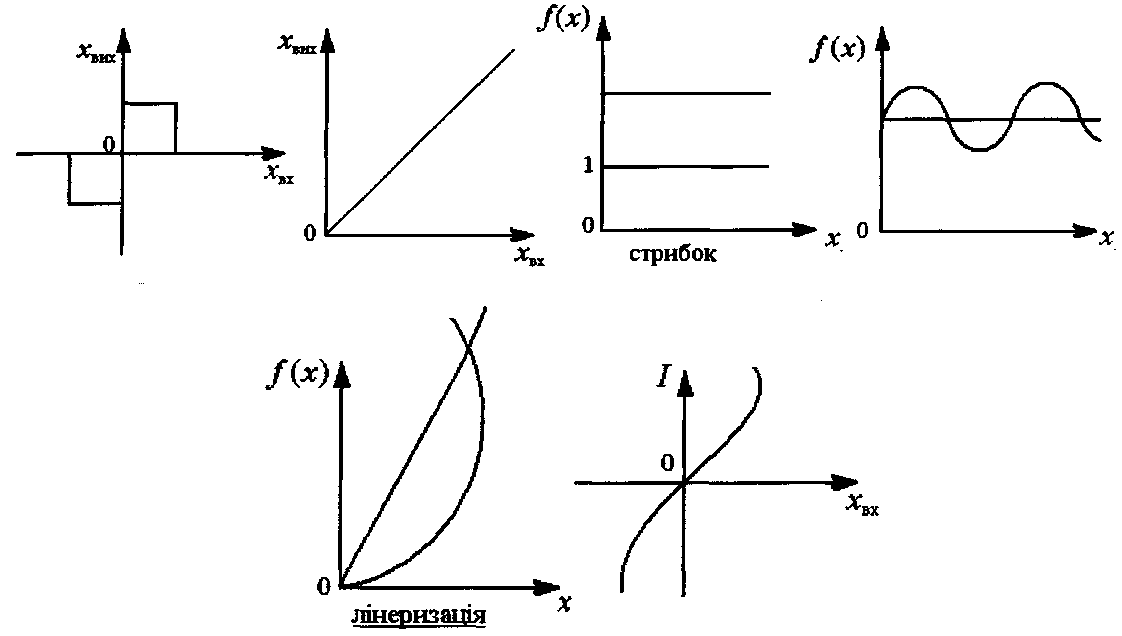
![]()
![]()
S ~ коефіцієнт кута нахилу прямої
3). Синусоїдальне діяння характеризує залежність
Найважливішими для автоматичних систем є ступінчасте діяння й одиничний стрибок.
2 години|