2. Изоэнтропийное течете газа в каналах турбомашин

Истечение газа при изоэнтропийном процессе его расширения подробно рассматривается в курсе термодинамики, поэтому здесь приведены лишь основные выводы.

Из уравнения энергии применительно к энергоизолированному расширению в турбинной решетке от давления Ро* до Р₁ без потерь

, (4.1)

где индекс t - указывает на то, что соответствующе параметры являются теоретическими, относящимися к расширению газа без потерь;

L_o1 - работа адиабатного расширения газа в решетке;

iо* - энтальпия, определенная по параметрам торможения (), то есть с учетом скорости на входе в сопло.

Параметры адиабатно заторможенного потока связаны со статическими параметрами известными формулами

, .

Учитывая выражение (2.34) и (2.37) получим

, (4.2)

, (4.3)

где - число Маха;

- приведенная скорость потока.

Рис. 4.1 Изоэнтропийный процесс расширения газа в соплах.

5. Действительный процесс течения рабочей среди.

Вследствие наличия вязкости действительный процесс истечения газа через сопло сопровождается трением частиц друг о друга, о стенки канала и вихреобразованием, что снижает скорость газа и уменьшает его кинетическую энергию. Вместе с тем, в энергоизолированном процессе по закону сохранения энергии потерянная кинетическая энергия превращается в тепло, вследствие чего температура и энтальпия протекающего газа повышаются.

Рис. 5.1 Процесс расширения газа в сопловом аппарате.

Действительный процесс расширения газа в сопле происходит по некоторой условной политропе Aо*A₁ (рис.5.1), причем в конечной точке процесса i₁ > i_1t. Действительная скорость на выходе из сопла С₁, очевидно, станет меньше теоретической С_1t. В действительном процессе скорость истечения определяется по выражению

.

Потеря кинетической энергии в сопле составит

или . (5.1)

Следует заметить, что потеря кинетической энергии оказывается меньше работы трения в соплах. Объясняется это тем, что часть работы трения в процессе расширения после превращения в тепловую энергию вновь превращается в кинетическую энергию. Эта часть работы трения называется возвращенным теплом.

Действительную скорость истечения из сопел можно определить по формуле

(5.2)

где φ - коэффициент скорости в соплах, который определяется опытным путем.

С использованием коэффициента φ потери энергии в соплах можно определить

, (5.3)

где - коэффициент потери энергии в сопле.

Очевидно, в действительном процессе расширения газа претерпят изменение, по сравнению со случаем истечения без потерь, и другие параметры газа, такие как температура, плотность, а также расход рабочего тела.

При заданном перепаде давлений в сопловом аппарате (от Ро* до P₁) и известным потерям температура газа за соплами

, (5.4)

где T_1t - теоретическая температура газа в конце адиабатического расширения (см.рис.5.1).

Плотность газа и его удельный объем находим из уравнения состояния газа

. (5.5)

Процесс истечения газа из соплового аппарата можно рассчитать по законам политропного расширения газа, если известен показатель n условной политропы расширения (процесс Aо*A₁ на рис.5.1).

Связь между скоростным коэффициентом сопел φ и показателем политропы n приближенно может быть выражено следующим образам. В политропном процессе

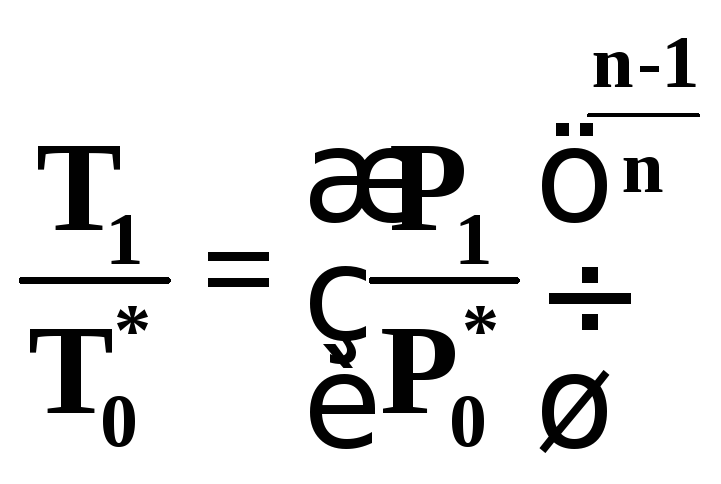. (5.6)

Предположим, что текущие параметры р и Т в процессе адиабатного расширения получили элементарное приращение. Тогда, из уравнения адиабатного процесса

. (5.7)

Разлагая левую часть равенства (5.7) в ряд Маклорена и ограничиваясь двумя членами разложения, получим

.

Если считать коэффициент величиной постоянной для всего процесса расширения, то из уравнения энергииследует, чтои тогда

После интегрирования получим

.

Сопоставляя выражение (5.8) и (5.6) можем записать

, (5.9)

или . (5.10)

Формулы (5.9) и (5.10) тем точнее, чем выше значение φ. Заметим, что при расширении газа всегда n < k.

Температуру в конце политропного расширения в соплах найдем из выражения (5.6)

.

Полезная работа расширения газа, которая может быть превращена в кинетическую энергию

. (5.11)

Скорость газа найдем из выражения, аналогичного (2.26)

, (5.12)

а расход газа - по формуле подобной (2.30)

. (5.13)

Изменится, очевидно, и критическое отношение давлений, которое на основе формулы (2.32) для течения с потерями примет вид

. (5.14)

В действительном процессе скорость звука в каждом из сечений станет больше (в связи с увеличением средней температуры от трения), а скорость потока меньше. Поэтому в минимальном сечении сопла Лаваля скорость потока уже не будет равна местной скорости звука. Равенство это наступит где-то за узким сечением сопла.

Расчетную формулу для определения величины минимального сечения сопла в действительном процессе можно получить, используя выражение (5.13) и (5.14)

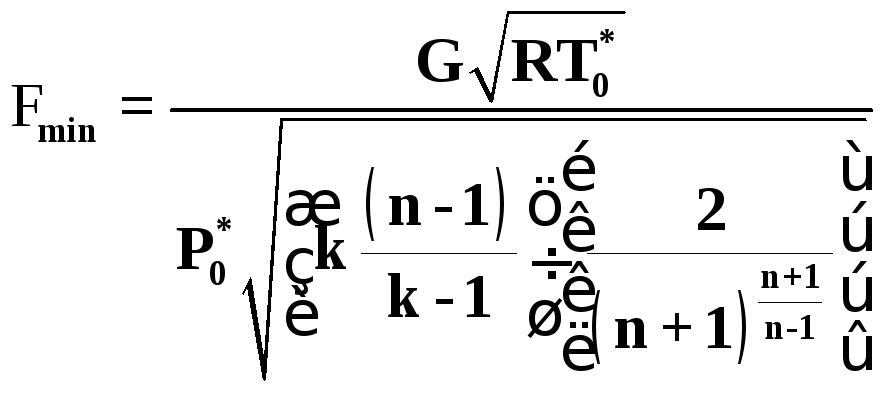(5.15)