
- •1. Определение первообразной.
- •2. Основные свойства неопределенного интеграла
- •6. Понятия о рациональных функциях
- •8. Интегрирование простейших дробей.
- •9. Интегрирование простейших дробей четвертого типа
- •10. Интегрирование тригонометрических функций.
- •12. Интегрирование иррациональных функций.
- •13. Дробно-линейная подстановка
- •14. Тригонометрическая подстановка
- •15. Определенный интеграл
- •18. Формула Ньютона-Лейбница.
- •19. Несобственные интегралы первого рода
- •20. Несобственные интегралы второго рода
- •22. Вычисление длины дуги плоской кривой
- •23. Вычисление объема тела, образованного вращением плоской фигуры вокруг оси
- •24. Определение двойного интеграла
22. Вычисление длины дуги плоской кривой
1
случай. Пусть в прямоугольных координатах
на плоскости дана кривая ![]() .
Вычислим длину дуги кривой, заключенной
между точками
.
Вычислим длину дуги кривой, заключенной
между точками![]() и
и![]() (рис.
12).
(рис.
12).

Возьмем
на дуге ![]() точки
точки![]() с
абсциссами
с
абсциссами![]() и
проведем хорды
и
проведем хорды![]() ,
длины которых обозначим соответственно
,
длины которых обозначим соответственно![]() .
Тогда получим ломанную
.
Тогда получим ломанную![]() ,
вписанную в дугу
,
вписанную в дугу![]() .
Длина ломанной равна
.
Длина ломанной равна
![]() .
.
Определение.
Длиной ![]() дуги
дуги![]() называется
тот предел, к которому стремится длина
вписанной ломанной, когда длина ее
наибольшего звена стремится к нулю:
называется
тот предел, к которому стремится длина
вписанной ломанной, когда длина ее
наибольшего звена стремится к нулю:
![]() .
.
Длина
всей дуги ![]() ,
заключенной между точками
,
заключенной между точками![]() и
и![]() ,
вычисляется по формуле
,
вычисляется по формуле
 .
.
Пример
16. Найти длину окружности ![]() .
.
Решение. Вычислим сначала длину четверти окружности, расположенной в 1 четверти.
Из
уравнения окрежности ![]() ,
,![]() .
.
Тогда ![]() .
.
Длина всей окрежности

Ответ: ![]() (лин.ед).
(лин.ед).
23. Вычисление объема тела, образованного вращением плоской фигуры вокруг оси
Пример 1
Вычислить
объем тела, полученного вращением
фигуры, ограниченной линиями ![]() ,
,![]() вокруг
оси
вокруг
оси![]() .
.
Решение:
Как и в задаче на нахождение площади, решение
начинается с чертежа плоской фигуры.
То есть, на плоскости ![]() необходимо
построить фигуру, ограниченную
линиями
необходимо
построить фигуру, ограниченную
линиями![]() ,
,![]() ,
при этом не забываем, что уравнение
,
при этом не забываем, что уравнение![]() задаёт
ось
задаёт
ось![]() .
Как рациональнее и быстрее выполнить
чертёж, можно узнать на страницахГрафики
и свойства Элементарных функцийи Определенный
интеграл. Как вычислить площадь фигуры.
Это китайское напоминание, и на данном
моменте я больше не останавливаюсь.
.
Как рациональнее и быстрее выполнить
чертёж, можно узнать на страницахГрафики
и свойства Элементарных функцийи Определенный
интеграл. Как вычислить площадь фигуры.
Это китайское напоминание, и на данном
моменте я больше не останавливаюсь.
Чертёж здесь довольно прост:
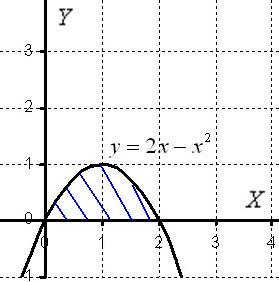
Искомая
плоская фигура заштрихована синим
цветом, именно она и вращается вокруг
оси ![]() В
результате вращения получается такая
немного яйцевидная летающая тарелка,
которая симметрична относительно оси
В
результате вращения получается такая
немного яйцевидная летающая тарелка,
которая симметрична относительно оси![]() .
На самом деле у тела есть математическое
название, но по справочнику что-то лень
уточнять, поэтому едем дальше.
.
На самом деле у тела есть математическое
название, но по справочнику что-то лень
уточнять, поэтому едем дальше.
Как вычислить объем тела вращения?
Объем тела вращения можно вычислить по формуле:

В
формуле перед интегралом обязательно
присутствует число ![]() .
Так повелось – всё, что в жизни крутится,
связано с этой константой.
.
Так повелось – всё, что в жизни крутится,
связано с этой константой.
Как расставить пределы интегрирования «а» и «бэ», думаю, легко догадаться из выполненного чертежа.
Функция ![]() …
что это за функция? Давайте посмотрим
на чертеж. Плоская фигура ограничена
графиком параболы
…
что это за функция? Давайте посмотрим
на чертеж. Плоская фигура ограничена
графиком параболы![]() сверху.
Это и есть та функция, которая
подразумевается в формуле.
сверху.
Это и есть та функция, которая
подразумевается в формуле.
В
практических заданиях плоская фигура
иногда может располагаться и ниже оси ![]() .
Это ничего не меняет – подынтегральная
функция в формуле возводится в квадрат:
.
Это ничего не меняет – подынтегральная
функция в формуле возводится в квадрат:![]() ,
таким образоминтеграл
всегда неотрицателен,
что весьма логично.
,
таким образоминтеграл
всегда неотрицателен,
что весьма логично.
Вычислим
объем тела вращения, используя данную
формулу:

Как я уже отмечал, интеграл почти всегда получается простой, главное, быть внимательным.
Ответ: ![]()
В
ответе нужно обязательно указать
размерность – кубические единицы ![]() .
То есть, в нашем теле вращения примерно
3,35 «кубиков». Почему именно
кубическиеединицы?
Потому что наиболее универсальная
формулировка. Могут быть кубические
сантиметры, могут быть кубические метры,
могут быть кубические километры и т.д.,
это уж, сколько зеленых человечков ваше
воображение поместит в летающую тарелку.
.
То есть, в нашем теле вращения примерно
3,35 «кубиков». Почему именно
кубическиеединицы?
Потому что наиболее универсальная
формулировка. Могут быть кубические
сантиметры, могут быть кубические метры,
могут быть кубические километры и т.д.,
это уж, сколько зеленых человечков ваше
воображение поместит в летающую тарелку.
24. Определение двойного интеграла
Понятие интеграла может быть расширено на функции двух и большего числа переменных. Рассмотрим, например, функцию двух переменных z = f (x,y). Двойной интеграл от функции f (x,y) обозначается как
![]()
где R -
область интегрирования в плоскости
Oxy.
Если определенный интеграл ![]() от
функции одной переменной
от
функции одной переменной![]() выражает
площадь под кривойf (x) в
интервале от x
= a до x
= b,
то двойной интеграл выражает объем под
поверхностью z
= f (x,y) выше
плоскости Oxy в
области интегрирования R (рисунок
1).
выражает
площадь под кривойf (x) в
интервале от x
= a до x
= b,
то двойной интеграл выражает объем под
поверхностью z
= f (x,y) выше
плоскости Oxy в
области интегрирования R (рисунок
1).
|
|
|
|
|
Рис.1 |
|
|
25. Геометрический смысл двойного интеграла. Если f(x,y) ?0 в области D, то двойной интеграл (1) равен объему “цилиндрического” тела, изображенного на рис.1:
V =  (2)
(2)
Пояснение. Цилиндрическое тело ограничено снизу областью D, сверху - частью поверхности z=f(x,y), с боков - вертикальными отрезками прямых, соединяющих границы этой поверхности и области D.
26. Основные свойства двойного интеграла:
1. Постоянный множитель выносится за знак интегр.
2. Интеграл от суммы равен сумме интегралов
3.
Если область D
разбить на 2 части, то

27. Вычисление двойного интеграла в декартовых координатах
Пусть требуется вычислить двойной интегр. Где ф-ция f(x;y) непрерывна в области D
Пусть
область D
представляет собой криволин. Трапецию
ограниченную кривыми и прямыми D:
 ;x=a;
x=b
;x=a;
x=b
Такая область правильная в направлении оси OY, то есть любая прямая параллельная OY пересекает границу области на более чем в 2-х точках
Если область правильная, тогда вычисление 2-го интегр. сводится к вычислению двукратного (повторного) интеграла.

28. Замена переменной в двойном интеграле. Вычисление двойного интеграла в полярных координатах
Заменим
независимые переменные х и у через
функцию
 ;
; ,
если эти функции имеют в некоторой
области
,
если эти функции имеют в некоторой
области непрерывные частные производные и
отличный от нуля определитель
непрерывные частные производные и
отличный от нуля определитель

А f(x;y) интегрируема в области D, тогда имеет место замена переменных
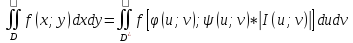
I(u;v) – определитель Якоби (якобиан)
Пусть в полярных координатах
x=rcosφ
y=rsinφ
I(φ;r)=-r
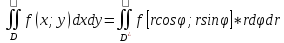
Пусть
область
 ограничена
лучами
ограничена
лучами ,
, и кривыми
и кривыми

29. Физические приложения двойного интеграла
Физический смысл двойного интеграла заключен в нахождении массы плоской пластины

30. Определение криволинейного интеграла 1 рода
Если существует предел интегральной суммы, который не зависит ни от способа разбиения кривой на части, ни от выбора в них точек, то он называется криволинейный интеграл от ф-ции f(x;y) по длине кривой AB
31. Основные свойства криволинейного интеграла 1 рода
1. Постоянный множитель выносится за знак интегр.
2. Интеграл от суммы равен сумме интегралов
3. Если кривую АВ разбить на части такие, что их объединение = АВ и они имеют только 1 общую точку разделяющую их, тогда

4. Криволинейный интеграл 1-го порядка не зависит от направления пути направления кривой
32. Вычисление криволинейного интеграла 1 рода
а. Параметрическое представление кривой



б. Явно заданная функция
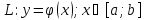
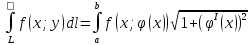
33. Приложения криволинейного интеграла 1 рода
1. Длина кривой

2. Площадь цилиндрической поверхности
Если
направляющей цилиндрической поверхности
служит кривая АВ, а образующая параллельна
оси OZ,
то площадь такой поверхности z=f(x;y)
вычисляется по формуле

3. Масса плоской кривой (провод)

4. Статические моменты

5. Координаты центра тяжести

6. Момент инерции

34. Определение криволинейного интеграла 2 рода
Предположим,
что кривая C задана векторной
функцией  ,
где переменная s − длина дуги
кривой. Тогда производная векторной
функции
,
где переменная s − длина дуги
кривой. Тогда производная векторной
функции

представляет собой единичный вектор, направленный вдоль касательной к данной кривой. В приведенной выше формуле α, β и γ − углы между касательной и положительными направлениями осей Ox, Oy и Oz, соответственно.
Введем векторную функцию F(P;Q;R), определенную на кривой C, так, чтобы для скалярной функции

существовал
криволинейный интеграл  .
Такой интеграл называетсякриволинейным
интегралом второго
рода от
векторной функции
.
Такой интеграл называетсякриволинейным
интегралом второго
рода от
векторной функции ![]() вдоль
кривойC и
обозначается как
вдоль
кривойC и
обозначается как

35. Основные свойства криволинейного интеграла 2 рода
1. Если в КИ2 изменить направление интегрирования, то он поменяет знак на противоположный
2. Если кривая АВ разбита точкой С на части, то

3. Если кривая лежит в плоскости перпендикулярной ОХ, то

Аналогично для OY
4. Криволинейный интеграл по замкнутой кривой не зависит от выбора начальной точки, а зависит только от направления обхода прямой
36. Вычисление криволинейного интеграла 2 рода
а. Параметрическое представление кривой




б. Явно заданная функция





37. Приложения криволинейного интеграла 2 рода
C помощью криволинейных интегралов вычисляются:
- Масса кривой
- Центр масс и моменты инерции кривой
- Работа при перемещении тела в силовом поле
- Магнитное поле вокруг проводника с током (Закон Ампера)
- Электромагнитная индукция в замкнутом контуре при изменении магнитного потока (Закон Фарадея)
38. Формула Остроградского-Грина
Пусть на плоскости OXY задана область D, ограниченная кривой пересекающейся с прямыми параллельными координатным осям не более чем в 2-х точках то есть, область D правильная.
Если ф-ции P(x;y) и Q(x;y) непрерывны вместе со своими частными производными в области D, то имеет место формула:

39. Основные понятия о дифференциальных уравнениях (определение, решение, порядок, обыкновенные ДУ, ДУ в общих производных, вид, общее решение, частные решения, начальные условия, задача Коши)
40. ДУ с разделяющимися переменными
Среди
обыкновенных дифференциальных уравнений
первого порядка существуют такие, в
которых возможно переменные x и y разнести
по разные стороны знака равенства. В
уравнениях вида  переменные
уже разделены, а в ОДУ
переменные
уже разделены, а в ОДУ переменные
разделяются посредством преобразований.
Кроме того, некоторые дифференциальные
уравнения сводятся к уравнениям с
разделяющимися переменными после
введения новых переменных.
переменные
разделяются посредством преобразований.
Кроме того, некоторые дифференциальные
уравнения сводятся к уравнениям с
разделяющимися переменными после
введения новых переменных.
41. Однородные ДУ 1-го порядка
ДУ
вида
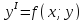 – однородныеn-го
порядка, если при умножении каждого
элемента функции на множитель t
вся функция умножится на
– однородныеn-го
порядка, если при умножении каждого
элемента функции на множитель t
вся функция умножится на


42. Линейные ДУ 1-го порядка. Метод вариации произвольной постоянной
Линейные ДУ 1-го порядка имеют такой вид

Характерная особенность – функция и ее производные входят в уравнение в 1 степени и между собой не перемножаются
Метод Лагранжа (Метод вариаций произвольной постоянной)
Метод вариации произвольной постоянной состоит в том, что постоянную С в полученном решении заменяем С=с(x), тогда решение исходного уравнения будем искать в виде

После
находим производную
 и подставляем в исходное уравнение
и подставляем в исходное уравнение
43. Линейные ДУ 1-го порядка. Метод Бернулли
Линейные ДУ 1-го порядка имеют такой вид

Характерная особенность – функция и ее производные входят в уравнение в 1 степени и между собой не перемножаются
Метод Бернулли
Решение данного уравнения ищется в виде производной 2-х функция то, есть с помощью подстановки
y=U*V, где U=u(x) и V=v(x)
Подставим
выражение для y
и
 в исходное уравнение
в исходное уравнение

Сгруппируем 1 и 3 слогаемые, или 2 и 3 и вынесем общий множитель за скобки
 (*)
(*)
Функцию v подберём таким образом, чтобы выражение в скобках было равно нулю
 –уравнение
с разд. переменными, получаем:
–уравнение
с разд. переменными, получаем:

Подставляем полученное в уравнение (*), учитывая, что выражение в скобках равно нулю



Ответ:

44.
ДУ высших порядков, допускающие понижения
порядка. ДУ вида

Рассмотрим
дифференциальное уравнение вида ![]() ,
где
,
где![]() –
производная «энного» порядка, а правая
часть
–
производная «энного» порядка, а правая
часть![]() зависиттолько
от «икс».
В простейшем случае
зависиттолько
от «икс».
В простейшем случае ![]() может
быть константой.
может
быть константой.
Данное
дифференциальное уравнение решается
последовательным интегрированием
правой части. Причём интегрировать
придется ровно ![]() раз.
раз.
На
практике наиболее популярной разновидность
является уравнение второго порядка: ![]() .
Дважды интегрируем правую часть и
получаем общее решение. Уравнение
третьего порядка
.
Дважды интегрируем правую часть и
получаем общее решение. Уравнение
третьего порядка![]() необходимо
проинтегрировать трижды, и т.д.
необходимо
проинтегрировать трижды, и т.д.
45.
ДУ высших порядков, допускающие понижения
порядка. ДУ вида

Порядок
такого уравнения можно понизить
на ![]() единиц
заменой
единиц
заменой![]() .
Тогда уравнение примет вид
.
Тогда уравнение примет вид
![]()
Из
последнего уравнения, если это возможно,
определяем ![]() ,
а затем находим
,
а затем находим![]() из
уравнения
из
уравнения![]() k-кратным
интегрированием.
k-кратным
интегрированием.
46.
ДУ высших порядков, допускающие понижения
порядка. ДУ вида

Отличительная особенность данного диффура состоит в том, что в нём в явном виде отсутствует независимая переменная «икс». То есть, в исходном дифференциальном уравнении нет «икса».
Подстановка ![]() позволяет
понизить порядок уравнения на единицу.
При этом
позволяет
понизить порядок уравнения на единицу.
При этом![]() рассматривается
как новая неизвестная функция от
рассматривается
как новая неизвестная функция от![]() .
Все производные
.
Все производные![]() выражаются
через производные от новой неизвестной
функции
выражаются
через производные от новой неизвестной
функции![]() по
по![]()


Подставив
эти выражения вместо ![]() в
уравнение, получим дифференциальное
уравнение (n–1)-го порядка
в
уравнение, получим дифференциальное
уравнение (n–1)-го порядка
47. Линейные однородные ДУ второго порядка. Определитель Вронского. Структура общего решения
Рассмотрим линейное дифференциальное уравнение вида
![]()
где p, q − постоянные коэффициенты. Для каждого такого дифференциального уравнения можно записать так называемое характеристическое уравнение:
![]()
Общее решение однородного дифференциального уравнения зависит от корней характеристического уравнения, которое в данном случае будет являться квадратным уравнением. Возможны следующие случаи:
Дискриминант характеристического квадратного уравнения положителен: D > 0. Тогда корни характеристического уравнения k1 и k2 действительны и различны. В этом случае общее решение описывается функцией
![]()
где C1 и C2 − произвольные действительные числа.
Дискриминант характеристического квадратного уравнения равен нулю: D = 0. Тогда корни действительны и равны. В этом случае говорят, что существует один корень k1 второго порядка. Общее решение однородного дифференциального уравнения имеет вид:
![]()
Дискриминант характеристического квадратного уравнения отрицателен: D < 0. Такое уравнение имеет комплексно-сопряженные корни k1 = α + βi, k1 = α − βi. Общее решение записывается в виде
![]()
48. Интегрирование ЛОДУ второго порядка с постоянными коэффициентами

Эйлер предложил искать частные решения в виде:
 k
– некоторое число
k
– некоторое число

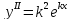

 –характеристическое
уравнение
–характеристическое
уравнение
Случ.1
D>0
=>

Общее
решение записываем в виде

Случ.2
D=0
=>


Случ.3
D<0
=>

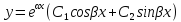
49.
Интегрирование ЛНДУ второго порядка с
постоянными коэффициентами. Случай

Общее решение ЛНДУ выглядит так:

Для ЛНДУ с правой частью специального вида частное решение можно найти пользуясь методом неопределённых коэффициентов. Суть метода: по виду правой части уравнения запишем ожидаемую форму частного решения с неопределённым коэффициентом, затем дважды её продифференцируем и полученные выражения подставим в исходное уравнение после чего найдём неопределённые коэффициенты
Частное для такого уравнения будет находиться в виде

r – число равное кратности α, как корня характеристического уравнения
а.
Если


б.
Если


в.
Если


50.
Интегрирование ЛНДУ второго порядка с
постоянными коэффициентами. Случай

Общее решение ЛНДУ выглядит так:
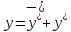
Для ЛНДУ с правой частью специального вида частное решение можно найти пользуясь методом неопределённых коэффициентов. Суть метода: по виду правой части уравнения запишем ожидаемую форму частного решения с неопределённым коэффициентом, затем дважды её продифференцируем и полученные выражения подставим в исходное уравнение после чего найдём неопределённые коэффициенты


l = max (n;m)
r
– число равное кратности
 как корень характеристического уравнения
как корень характеристического уравнения


