8. Интегрирование простейших дробей.

Задача нахождения неопределенного интеграла дробно рациональной функции сводится к интегрированию простейших дробей. Поэтому рекомендуем для начала ознакомиться с разделом теории разложение дроби на простейшие.

Пример.

Найти неопределенный интеграл .

Решение.

Так как степень числителя подынтегральной функции равна степени знаменателя, то для начала выделяем целую часть, проводя деление столбиком многочлена на многочлен:

Поэтому, .

Разложение полученной правильной рациональной дроби на простейшие дроби имеет вид. Следовательно,

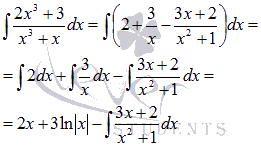
Полученный интеграл представляет собой интеграл простейшей дроби третьего типа. Забегая немного вперед, отметим, что взять его можно методом подведения под знак дифференциала.

Так как , то. Поэтому

Следовательно, 

Теперь перейдем к описанию методов интегрирования простейших дробей каждого из четырех типов.

Интегрирование простейших дробей первого типа 

Для решения этой задачи идеально подходит метод непосредственного интегрирования:

Пример.

Найти множество первообразных функции 

Решение.

Найдем неопределенный интеграл , используя свойства первообразной, таблицу первообразных и правило интегрирования.

К началу страницы

Интегрирование простейших дробей второго типа 

Для решения этой задачи также подходит метод непосредственного интегрирования:

Пример.

Найдите неопределенный интеграл .

Решение.

К началу страницы

Интегрирование простейших дробей третьего типа 

Для начала представляем неопределенный интеграл 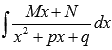в виде суммы:

Первый интеграл берем методом подведения под знак дифференциала: 

Поэтому, 

У полученного интеграла преобразуем знаменатель:

Следовательно, 

Формула интегрирования простейших дробей третьего типа принимает вид: 

Пример.

Найдите неопределенный интеграл .

Решение.

Используем полученную формулу: 

Если бы у нас не было этой формулы, то как бы мы поступили: 

9. Интегрирование простейших дробей четвертого типа

Первый шаг – подводим под знак дифференциала: 

Второй шаг – нахождение интеграла вида . Интегралы подобного вида находятся с использованием рекуррентных формул. (Смотрите разделинтегрирование с использованием рекуррентных формул). Для нашего случая подходит следующая рекуррентная формула:

Пример.

Найдите неопределенный интеграл 

Решение.

Для данного вида подынтегральной функции используем метод подстановки. Введем новую переменную (смотрите раздел интегрирование иррациональных функций):

После подстановки имеем: 

Пришли к нахождению интеграла дроби четвертого типа. В нашем случае имеем коэффициенты М = 0, р = 0, q = 1, N = 1 и n = 3. Применяем рекуррентную формулу: 

После обратной замены получаем результат:

10. Интегрирование тригонометрических функций.

Множество задач сводится к нахождению интегралов трансцендентных функций, содержащих тригонометрические функции. В данной статье сгруппируем наиболее часто встречающиеся виды подынтегральных функций и на примерах рассмотрим методы их интегрирования.

• Начнем с интегрирования синуса, косинуса, тангенса и котангенса.

Из таблицы первообразных сразу заметим, что и.

Метод подведения под знак дифференциалапозволяет вычислить неопределенные интегралы функций тангенса и котангенса:

К началу страницы

• Поясним, как были найдены формулы и, находящиеся в таблице первообразных.

Разберем первый случай, второй абсолютно аналогичен.

Воспользуемся методом подстановки:

Пришли к задаче интегрирования иррациональной функции. Здесь нам также поможет метод подстановки:

Осталось провести обратную замену иt = sinx: 

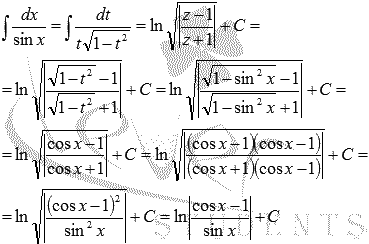
К началу страницы

• Отдельно хочется остановиться на интегралах, содержащих степени тригонометрических функций, вида .

Подробно о принципах их нахождении можете ознакомиться в разделеинтегрирование с использованием рекуррентных формул. Если изучите вывод этих формул, то без особого труда сможете брать интегралы вида, гдеm и n – натуральные числа.

К началу страницы

• Когда тригонометрические функции идут в комбинациях с многочленами или показательными функциями, то применяется метод интегрирования по частям. В этом разделе даны рекомендации для нахождения интегралов,.

К началу страницы

• Максимум творчества приходится вкладывать, когда подынтегральная функция содержит тригонометрические функции с различными аргументами.

Здесь на помощь приходят основные формулы тригонометрии. Так что выписывайте их на отдельный листочек и держите перед глазами.

Пример.

Найти множество первообразных функции .

Решение.

Формулы понижения степени дают и.

Поэтому 

Знаменатель представляет собой формулу синуса суммы, следовательно, 

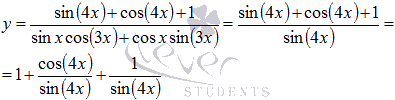
Приходим к сумме трех интегралов. 

К началу страницы

• Подынтегральные выражения, содержащие тригонометрические функции, иногда можно свести к дробно рациональным выражениям, используя стандартную тригонометрическую подстановку.

Выпишем тригонометрические формулы, выражающие синус, косинус, тангенс через тангенс половинного аргумента: 

При интегрировании нам также понадобится выражение дифференциала dx через тангенс половинного угла.

Так как , то

То есть, , где.

Пример.

Найти неопределенный интеграл .

Решение.

Применим стандартную тригонометрическую подстановку: 

Таким образом, .

Разложение на простейшие дробиподынтегральной функции приводит нас к сумме двух интегралов:

Осталось провести обратную замену :

11. Рекуррентные формулы – это формулы, выражающие n-ый член последовательности через предыдущие члены. При нахождении интегралов они не редко используются.

Мы не ставим целью перечислить все рекуррентные формулы, а хотим дать принцип их получения. Вывод этих формул основан на преобразовании подынтегральной функции и применении метода интегрирования по частям.

К примеру, неопределенный интеграл можно взять, используя рекуррентную формулу.

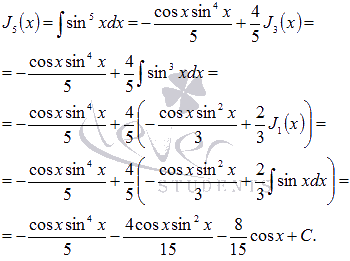
Вывод формулы :

Используя формулы тригонометрии, можно записать:

Полученный интеграл найдем методом интегрирования по частям. В качестве функции u(x)возьмем cosx, следовательно, .

Поэтому,

Возвращаемся к исходному интегралу:

То есть, 

Что и требовалось показать.

Аналогично выводятся следующие рекуррентные формулы:

1. Для нахождения интегралов вида используется рекуррентная формула,n – натуральное число.

2. Для нахождения интегралов вида используется рекуррентная формула.

3. Для нахождения интегралов вида используется рекуррентная формула.

4. Для нахождения интегралов вида используется рекуррентная формула.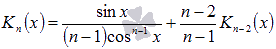

Пример.

Найти неопределенный интеграл .

Решение.

Используем рекуррентную формулу из четвертого пункта (в нашем примере n = 3):

Так как из таблицы первообразных имеем , то