Lab_02

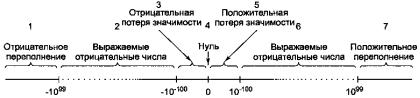
Числа с плавающей точкой можно использовать для моделирования системы действительных чисел в математике, хотя здесь есть несколько существенных различий. На рис. 1 представлена ось действительных чисел. Она разбита на 7 областей:

1.Отрицательные числа меньше -0,999 × 1099.

2.Отрицательные числа от -0,999 × 1099 до -0,100 × 10-99.

3.Отрицательные числа от -0,100 × 10-99 до нуля.

4.Нуль.

5.Положительные числа от 0 до 0,100 × 10-99.

6.Положительные числа от 0,100 × 10-99 до 0,999 × 1099.

7.Положительные числа больше 0,999 × 1099.

Рисунок 1 - Ось действительных чисел разбита на 7 областей

Первое отличие действительных чисел от чисел с плавающей точкой, которые записываются тремя разрядами в мантиссе и двумя разрядами в экспоненте, состоит в том, что последние нельзя использовать для записи чисел из областей 1, 3, 5 и 7. Если в результате арифметической операции получится число из области 1 или 7 (например, 1060 × 1060 = 10120), то произойдет ошибка переполнения и результат будет неверным. Причина – ограничение области значений чисел в данном представлении. Точно так же нельзя выразить результат из области 3 или 5. Такая ситуация называется ошибкой потери значимости. Эта ошибка менее серьезна, чем ошибка переполнения, поскольку часто нуль является вполне удовлетворительным приближением для чисел из областей 3 или 5. Остаток счета в банке на 10-102 не сильно отличается от нулевого остатка счета.

Второе важное отличие чисел с плавающей точкой от действительных чисел – их плотность. Между любыми двумя действительными числами x и y существует другое действительное число независимо от того, насколько близко к y расположено число x. Это свойство вытекает из того, что для любых отличных действительных чисел x и y между ними существует действительное число z = (x + y) / 2. Действительные числа формируют континуум.

Числа с плавающей точкой континуума не формируют. В двухзнаковой пятиразрядной системе можно выразить ровно 179 100 положительных чисел, 179 100 отрицательных чисел и 0 (который можно выразить разными способами), то есть всего 358 201 чисел. Из бесконечного числа действительных чисел в диапазоне от -10+100 до +0,999 × 1099 в этой системе можно выразить только 358 201 число. На рис. 1 эти числа показаны точками. Результат

2

вычислений может быть и другим числом, даже если он находится в области 2 или 6. Например, результат деления числа +0,100 × 103 на 3 нельзя выразить точно в нашем представлении. Если полученное число нельзя выразить с помощью используемого представления, нужно брать ближайшее представимое число. Такой процесс называется округлением.

Промежутки между смежными числами, которые можно выразить в представлении с плавающей точкой, в областях 2 и 6. не постоянны. Промежуток между числами +0,998 × 1099 и +0,999 × 1099 гораздо больше промежутка между числами +0,998 × 100 и +0,999 × 100. Однако если промежутки между числом и его соседом выразить как процентное отношение от этого числа, большой разницы в промежутках не будет. Другими словами, относительная погрешность, полученная при округлении, приблизительно равна и для малых, и для больших чисел.

Выводы, сделанные для системы представления с трехразрядной мантиссой и двухразрядной экспонентой, справедливы и для других представлений чисел. При изменении числа разрядов в мантиссе или экспоненте просто сдвигаются границы областей 2 и 6, и меняется число представляемых единиц в этих областях. С увеличением числа разрядов в мантиссе увеличивается плотность элементов и, следовательно, точность приближения. С увеличением количества разрядов в экспоненте области 2 и 6 увеличиваются за счет уменьшения областей 1, 3, 5 и 7. В табл. 1 показаны приблизительные границы области 6 для десятичных чисел с плавающей точкой и различным количеством разрядов в мантиссе и экспоненте.

Таблица 1. Приблизительные верхняя и нижняя границы чисел с плавающей точкой

Вариант такого представления применяется в компьютерах. Основа возведения в степень – 2, 4, 8 или 16, но не 10. В этом случае мантисса состоит из цепочки двоичных, четверичных, восьмеричных и шестнадцатеричных

3

разрядов. Если крайний левый разряд равен 0, то все разряды можно сместить на один влево, а экспоненту уменьшить на 1, не меняя при этом значения числа (исключение составляет ситуация потери значимости). Мантисса с ненулевым крайним левым разрядом называется нормализованной.

Нормализованные числа обычно предпочитаются ненормализованным, поскольку существует только одна нормализованная форма, а ненормализованных форм может быть много. Примеры нормализованных чисел с плавающей точкой даны на рис. 2 для двух оснований степени. В этих примерах показана 16-разрядная мантисса (включая знаковый бит) и 7-разрядная экспонента. Точка находится слева от крайнего левого бита мантиссы и справа от экспоненты.

Рисунок 2 - Примеры нормализованных чисел с плавающей точкой

4

2.1. Стандарт IEEE 754

До 80-х годов каждый производитель поддерживал собственный формат чисел с плавающей точкой. Все они отличались друг от друга. Более того, в некоторых из них арифметические действия выполнялись неправильно, поскольку арифметика с плавающей точкой имеет некоторые тонкости, которые не очевидны для среднестатистического разработчика аппаратного обеспечения.

Чтобы изменить эту ситуацию, в конце 70-х годов институт IEEE учредил комиссию по стандартизации арифметики с плавающей точкой. Целью было не только дать возможность переносить данные с одного компьютера на другой, но и обеспечить разработчиков аппаратного обеспечения заведомо правильной моделью. В результате в 1985 г. вышел стандарт IEEE 754. В настоящее время большинство процессоров (в том числе Intel, SPARC и JVM) содержат команды с плавающей точкой, которые соответствуют этому стандарту.

Стандарт IEEE 754 определяет четыре формата: с одинарной точностью

(single-precision) 32 бита, с удвоенной точностью (double-precision) 64 бита, с

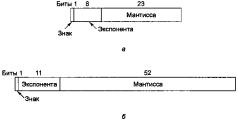
одинарной расширенной точностью (single-extended precision) ≥ 43 бит (редко используемый) и с двойной расширенной точностью (double-extended precision) ≥ 79 бит (обычно используют 80 бит). Формат с повышенной точностью предназначен для уменьшения ошибки округления. Он применяется главным образом в арифметических устройствах с плавающей точкой, поэтому мы не будем о нем говорить. Основное применение в технике и программировании получили форматы 32 и 64 бита. Например, в основных логических языках VB и C используют типы данных single и double. Тип double является просто увеличенной копией single. В форматах с одинарной и удвоенной точностью используются основание степени 2 для мантисс и смещенная экспонента. Форматы представлены на рис. 3.

Рисунок 3 - Форматы стандарта IEEE с плавающей точкой: одинарная точность (а); удвоенная точность (б)

Оба формата начинаются со знакового бита для всего числа; 0 указывает на положительное число, 1 – на отрицательное. Затем следует смещенная экспонента. Для формата одинарной точности смещение равно 127, а для формата удвоенной точности – 1023. Минимальная (0) и максимальная (255 и 2047) экспоненты не используются для нормализованных чисел. У них есть

5

специальное предназначение, о котором мы поговорим позже. В конце идут мантиссы по 23 и 52 бита соответственно.

Нормализованная мантисса начинается с двоичной точки, за которой следует 1 бит, а затем – остаток мантиссы. Следуя практике, начатой с компьютера PDP-11, компьютерщики осознали, что 1 бит перед мантиссой сохранять не нужно, а нужно просто считать, что он там есть. Следовательно, стандарт определяет мантиссу следующим образом. Она состоит из неявного бита, который всегда равен 1, и неявной двоичной точки, за которыми идут 23 или 52 произвольных бита. Если все 23 или 52 бита мантиссы равны 0, то мантисса имеет значение 1,0. Если все биты мантиссы равны 1, то числовое значение мантиссы немного меньше, чем 2,0. Во избежание путаницы в английском языке для обозначения комбинации из неявного бита, неявной двоичной точки и 23 или 52 явных битов вместо термина мантисса (mantissa) используется термин значащая часть числа (significant). Значащая часть числа (s) всех нормализованных чисел лежит в диапазоне 1 ≤ s < 2.

Числовые характеристики стандарта IEEE для чисел с плавающей точкой даны в табл. 2.

Таблица 2. Характеристики чисел с плавающей точкой стандарта IEEE

Пример 1. Преобразовать десятичное число 155,62510 в 32 битный формат стандарта IEEE 754.

Наша задача сводится к представлению десятичного числа с плавающей точкой в двоичное с плавающей точкой в экспоненциальном нормализованном виде.

155.625 = 1×27 + 0×26 + 0×25 + 1×24 + 1×23 + 0×22 + 1×21 + 1×20 + 1×2-1 + 0×2-2 + 1×2-3. 155.625 = 128 + 0 + 0 + 16 + 8 + 0 + 2 + 1 + 0,5 + 0 + 0.125.

155.62510 = 10011011.1012.

1.55625e+210 = 1.0011011101e+1112.

В результате мы получим число в двоичном коде: ma = 1.0011011101 (мантисса),

pa = 111 (порядок по основанию 2).

Далее преобразуем полученное двоичное число с плавающей точкой в 32 битный формат стандарта IEEE 754. Однако существуют следующие тонкости:

6

1.Число может быть ±. Поэтому отведем 1 бит для обозначения знака числа: 0-положительное, 1-отрицательное (этот бит будет самый старший в 32 битной последовательности).

2.Далее пойдут биты экспоненты, для этого выделим 1 байт (8 бит), но экспонента тоже может быть ±. Для определения знака экспоненты, чтобы не вводить ещё один бит знака, добавим смещение к экспоненте +127 (0111 1111 – это половина пространства отведенного под экспоненту). Это означает, что если наша экспоната = +7 (+111 в двоичной), то смещенная экспонента = 127 + 7 = 134. А если бы наша экспонента была -7, то смещенная экспонента = 127 - 7 = 120. Смещенную экспоненту мы и будем записывать в отведенные 8 бит. Тогда когда нам будет нужно получить экспоненту, мы просто отнимем 127 от этого байта.

3.Оставшиеся 23 бита мы отводим для мантиссы. Но, у нормализованной двоичной мантиссы первый бит всегда равен 1, т. к. число лежит в

Из этого 32 битного числа мы сможем восстановить десятичное число с плавающей точкой, так как мы знаем все параметры представленного числа.

Приведем формулу для восстановления числа из стандарта IEEE754 для одинарной точности (single):

где S- бит знака (31 бит), pa- смещенная экспонента (23-30 биты), ma- остаток от мантиссы (0-22 биты), F- десятичное число с плавающей точкой.

Выполним проверку:

F = (-1)0 × 2(134 - 127) × (1 + 1 810 432 / 8 388 608) = 27 × (1 + 0.2158203125) = 155.625.

Поясним, что (1+ ma / 223) – это мантисса, единица в этой формуле – это та единица, которую мы выбросили из 23 бит, а остаток мантиссы в десятичном виде находим отношением двух целых чисел – остатка мантиссы к целому).

Общая формула для вычисления нормализованных десятичных чисел с плавающей точкой из чисел представленных в стандарте IEEE 754:

7

где S- бит знака, pa- смещенная экспонента, b- количество разрядов отводимых для представления экспоненты, ma- остаток от мантиссы, n- количество разрядов отводимых для представления остатка от мантиссы, F- десятичное число с плавающей точкой.

Исключения чисел формата IEEE 754 из алгоритма вычисления по формуле 1.

Если применить формулу 1 для вычисления минимального и максимального числа представленного в IEEE 754, то получим следующие результаты:

00 00 00 00 hex = 5,87747175411144e-39 (минимальное положительное число);

80 00 00 00 hex = -5,87747175411144e-39 (минимальное отрицательное число);

3. числа IEEE 754 = FF (1xxx)X XX XX hex не считаются числами (NAN),

кроме случая п. 2

числа IEEE 754 = 7F (1xxx)X XX XX hex не считаются числами (NAN),

кроме случая п. 2

31 22 15 7 0

x 1 1 1 1 1 1 1 1 x x x x x x x x x x x x x x x x x x x x x x x

Число представленное в битах 0..22 может быть любым числом, кроме 0. 4. числа IEEE 754 = (x000) (0000) (0xxx)X XX XX hex считаются

денормализованными числами, за исключением чисел п. 1, т. е. -0 и +0

8

Общая формула для вычисления денормализованных десятичных чисел с плавающей точкой из чисел представленных в стандарте IEEE 754:

где S- бит знака, pa- смещенная экспонента, b- количество разрядов отводимых для представления экспоненты, ma- остаток от мантиссы, n- количество разрядов отводимых для представления остатка от мантиссы, F- десятичное число с плавающей точкой.

Полный диапазон чисел представленных в формате 32 бит по стандарту

IEEE 754:

- нулевые числа - денормализованные числа (рассчитываются по формуле 2)

- нормализованные числа (рассчитываются по формуле 1) - бесконечность

- не числа (NANs)

Если бесконечность разделить на бесконечность, то результат не определен. В этом случае существует другой специальный формат – не число (Not a Number, NaN). Его тоже можно использовать в качестве операнда.

3. Третья форма представления двоичных чисел – двоично-десятичная. Ее появление объясняется следующим. При обработке больших массивов десятичных чисел (например, больших экономических документов) приходится тратить много времени на перевод этих чисел из десятичной системы счисления в двоичную для последующей обработки и обратно – для вывода результатов. Каждый такой перевод требует выполнения двух – четырех десятков машинных команд. С включением в состав отдельных ЭВМ специальных функциональных блоков или спецпроцессоров десятичной арифметики появляется возможность обрабатывать десятичные числа напрямую, без их преобразования, что сокращает время вычислений. При этом каждая цифра десятичного числа

9

представляется двоичной тетрадой. Например, A10 = 3759, A2-10 = 0011 0111 0101 1001. Положение десятичной точки (запятой), отделяющей целую часть от дробной, обычно заранее фиксируется. Значение знака числа отмечается кодом, отличным от кодов цифр. Например, знак «+» имеет значение тетрады «1100», а

знак «-» – «1101».

Содержание отчета

1.Краткие теоретические сведения, необходимые для выполнения заданий и ответа на контрольные вопросы.

2.Полные ответы на контрольные вопросы и решения при выполнении заданий.

3.Выводы по работе.

Контрольные вопросы и задания

1. Преобразуйте следующие числа в формат стандарта IEEE 754 с одинарной точностью. Результаты представьте в восьми шестнадцатеричных разрядах.

IBM/370 состоят из 7-разрядной смещенной экспоненты (смещение равно 64), 24-разрядной мантиссы и знакового бита. Двоичная точка находится слева от мантиссы. Основание степени – 16. Порядок полей – знаковый бит, экспонента, мантисса. Выразите число 7/64 в виде нормализованного шестнадцатеричного числа в этой системе.

4. Следующие двоичные числа с плавающей точкой состоят из знакового бита, смещенной экспоненты (смещение равно 64) с основанием 2 и 16-разрядной мантиссы. Нормализуйте их:

10