[ООП] / Лекции / Lecture_10

Умножая слева и справа это уравнение на D−1

D−1Dx = D−1(D − A)x + D−1 f

ивведя новые обозначения : H = D−1(D − A) , d = D−1 f , окончательно получим:

x= Hx +d .

Сучетом полученной матричной формы метод Якоби можно записать как

Матрицу H называют переходной матрицей. Из полученных уравнений видно, что организовать решение линейной системы (1) можно путем циклического вычисления правой части уравнения (3) или (5). Причем, в последнем случае – это многократное умножение матрицы на вектор. Параллельные и векторные методы умножения матрицы на вектор мы рассматривали ранее.

Решение уравнения Пуассона методом Якоби

Итерационный метод Якоби применяется для решения краевых задач уравнений с частными производными, которые, в свою очередь, относятся к задачам математической физики.

Одной из задач такого типа является уравнение в частных производных, называемое уравнением Пуассона:

Если f (x, y)≡ 0 , то мы получим уравнение Лапласа. Не теряя общности, предположим, что х

и у принадлежат множеству вещественных чисел в диапазоне [0,1], которое образует прямоугольную область Ω на плоскости xy. Пусть функция u имеет начальные значения на границах области, а правая часть f (x, y)– заданная функция. Тогда эту задачу ещё называют зада-

чей Дирихле для уравнения Пуассона.

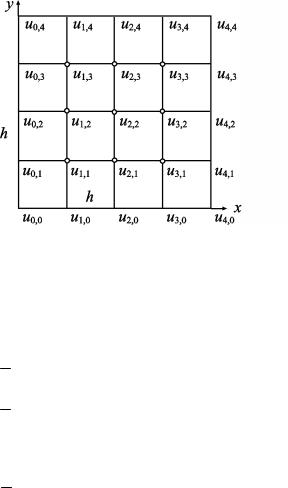
Используя выражения для конечных разностей и рассматривая область определения Ω как сетку с шагом h (рис.10.1), частные производные в уравнении Лапласа можно аппроксимировать центральными конечными разностями второго порядка:

Высокопроизводительные вычислительные системы и параллельное программирование. Кудерметов Р.К.

3

Рис.10.1

Если выражения (7) подставить в уравнение Пуассона, то, пренебрегая членами второго порядка малости, получим:

Записав это соотношение для каждой точки с учётом того, что начальные условия на границах области заданы, получим систему из M -1 линейных уравнений. Эту систему можно решить методом Якоби. Для этого перепишем систему (8) в виде:

Обратите внимание, что каждая итерация в точке сетки есть среднее арифметическое четырёх соседних точек предыдущей итерации минус некоторая заданная функция.

M 2

Рассмотрим возможные реализации метода Якоби для решения задачи Дирихле для уравнения Пуассона. Если область определения решения представляет собой плоскость, со-

стоящую из M 2 узлов, а число процессоров равно Р, то каждый из них должен обработать

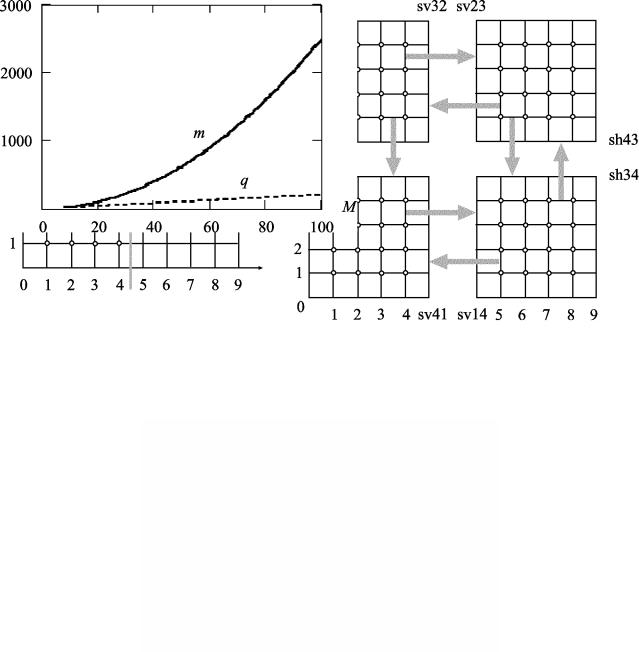
ближайшими соседями, причем, максимальное число соседей равно четырем, минимальное – двум. Число граничных узлов равно q = m = MP . Один из вариантов разбиения показан на

рис.10.2, где используется всего четыре процессора, а число узлов равно 64. Для этого случая на каждый процессор приходится по 16 узлов для обработки, а длина массива для обмена между двумя любыми процессорами равна 4. Очевидно, что при увеличении размера сетки числа узлов, подлежащих обработки увеличивается пропорционально квадрату размера сетки, а число узлов, между которыми необходимо произвести обмен данными – растет по линейному закону. Таким образом, при некотором размере сетки время затрачиваемое на вычисления будет превосходить время, необходимое на пересылки данных и, следовательно ускорение станет выше единицы, т.е. применение параллельной вычислительной системы станет эффективным.

Для организации параллельных вычислений, как показано на рисунке, необходимо ввести дополнительные слои, называемые теневыми (обозначены как sh и sv), которые обеспе-

Высокопроизводительные вычислительные системы и параллельное программирование. Кудерметов Р.К.

4

чивают граничные условия для каждой области. В эти области после каждой итерации заносятся результаты, полученные для первого внутреннего слоя соседней области. На рис.10.3 показаны графики зависимости количества внутренних узлов m (объем вычислений) и граничных узлов q (объем пересылок) от размерности сетки M.

Рис.10.2

При выполнении итераций по методу Якоби необходимо отметить следующие два обстоятельства.

Рис.10.3

Если задача определена на трехмерной области, то не трудно показать, что объем вычислений с ростом размера сетки возрастает пропорционально кубу, а объем пересылок – пропорционально квадрату этого размера.

Отметим так же такое обстоятельство. Если выполняются условия сходимости (здесь их не рассматриваем) метода Якоби для конкретно решаемой системы, то задачу можно решать в асинхронном режиме, т.к. что отдельные ошибочные итерации, вызванные несвоевременным обменом между соседними областями разбиения не скажутся на окончательном результате, а могут лишь увеличить общее время вычислений.

Высокопроизводительные вычислительные системы и параллельное программирование. Кудерметов Р.К.

5

Векторизация метода Якоби

Рассмотрим реализацию метода Якоби для уравнения Пуассона на векторном процессоре. Для представления всех узлов сетки, включая граничные условия нам необходим массив размера (N+2)×(N+2). Тогда алгоритм можно записать так:

for(j=1;j<=N;j++)

for(i=1;i<=N;i++)

u[i][j]=0,25*(u[i][j+1]+ u[i][j-1]+ u[i+1][j]+ u[i-1][j]-f[i][j]);

Если длина векторных регистров в вычислителе позволяет, то процесс может быть организован так:

Рис.10.4

Процесс, показанный на рис.10.4. представляет всего лишь одну итерацию по одному столбцу рассматриваемой плоской сетки (рис.10.1). Ясно, что затем, необходимо аналогичные векторные операции провести с другими столбцами. Когда все столбцы будут пересчитаны, завершится первая итерация. Далее необходимо продолжить процесс, снова начиная с первого и т.д. пока не выполнится условие (4). Рассмотренная схема вычислений относится к случаю, когда длина векторных регистров процессора равна числу узлов вдоль одного измерения сетки. В реальных задачах, понятно, дрина регистра значительно меньше, поэтому всю сетку делят на слои, равные по ширине длине векторного регистра и вычисления выполняют по слоям. Крооме того, Итерационный процесс существенно может зависеть от других архитектурных особенностей процессора: числа векторных регистров, возможности совмещения арифметических операций с операциями загрузки и сдвига, наличия регистров для хранения промежуточных результатов.

Векторизация метода Якоби с использованием матричного умножения

Рассмотрим ещё одну возможность векторизации процесса решения уравнений типа Пуассона методом Якоби. Воспользуемся таким примером. Пусть имеется область, на которой ищется решение Ω=[0,1]*[0,1]; Разобьем её с шагом n следующим образом:

Высокопроизводительные вычислительные системы и параллельное программирование. Кудерметов Р.К.

6

Рис.10.5

Тогда можно составить 9 уравнений в центральных конечных разностях:

u11 = 14 (u01 +u21 +u10 +u12 −h2 f11); u12 = 14 (u02 +u22 +u11 +u13 −h2 f12 ); u13 = 14 (u03 +u23 +u12 +u14 −h2 f13 );

. . . . . . . . . . . . . . . . . . . . . .

u33 = 14 (u23 +u43 +u32 +u34 −h2 f33 );

Введём обозначения:

x1 = u11 , x2 =u12 , x3 =u13 , x4 = u21 , x5 =u22 , x6 = u23 , x7 = u31 , x8 = u32 , x9 = u33 .

Тогда запишем систему в виде:

4x1 − x2 +0 − x4 +0 +0 +0 +0 +0 =u01 +u10 −h2 f11 ; − x1 +4x2 − x3 +0 − x5 +0 +0 +0 +0 =u02 −h2 f12 ; 0 − x2 +4x3 +0 +0 − x6 +0 +0 +0 =u03 +u14 −h2 f13 ;

. . . .. . . . . . . . . . . . . . . . . . . . . .

0 +0 +0 +0 +0 − x6 +0 − x8 +4x9 =u34 +u43 −h2 f33 .

В матричном виде эта система будет иметь вид:

Ax = f ,

где

x = (x1, x2 ,K, x9 )Τ ;

Высокопроизводительные вычислительные системы и параллельное программирование. Кудерметов Р.К.

7