10.5 Резонанс струмів у коливальному контурі

Знайдемо закон зміни струму в коливальному контурі при сталому режимі вимушених коливань. Для цього візьмемо похідну за часом із заряду (10.12)

. (10.20)

Амплітуда струму теж залежить від частоти Ω

. (10.21)

Знайдемо резонансну частоту для струму.

.

Одержуємо, (10.22)

що резонанс струму має місце при частоті ω_о власних незгасаючих коливань і на відміну від резонансу напруг не залежить від коефіцієнта згасання. Резонансні криві для струму зображені на рис.10.5.

Із зростанням коефіцієнта згасання β амплітуда струму при резонансі зменшується.

6. Приклади розв’язку задач

Задача 1. Математичний маятник довжиною ℓ = 0,5 м , виведений із положення рівноваги, відхилився при першому коливанні на Х₁ =5 см, а при другому (в той же бік) – на Х₂ = 4 см. Знайти час релаксації τ згасаючого коливання.

Розв’язок. Логарифмічний декремент згасання . Тут Т – період згасаючих коливань

, де , а. Одержуємо . Підносимо до квадрату і знаходимо

. Звідки

Зауваження. Типовою помилкою є знаходження періоду Т коливань за формулою . Але цей вираз дає період То незгасаючих коливань.

Задача 2. Коливальний контур складається із конденсатора ємністю С = 2,22 нФ і котушки, яка намотана в один шар виток до витка мідним дротом діаметром d = 0,5 мм. Довжина котушки ℓ = 0,2 м. Знайти логарифмічний декремент згасання λ.

Розв’язок. Тут, як і в попередній задачі, важливо не забути, що у контурі виникають згасаючі коливання (активний опір R – це опір дроту

.

Тут у знаменнику за корінь винесений множник і скорочений.

Виразимо індуктивність L і активний опір дроту R через геометричні розміри котушки: довжину ℓ і діаметр перерізу D. Індуктивність довгого соленоїда (котушки) . Тут μ і μ_о характеристики магнітних властивостей осердя (у нас повітря), –загальна кількість витків. Опір дроту знайдемо за формулою .– питомий опір міді. Знаходимо відношенняі підставляємо у вираз для λ.

.

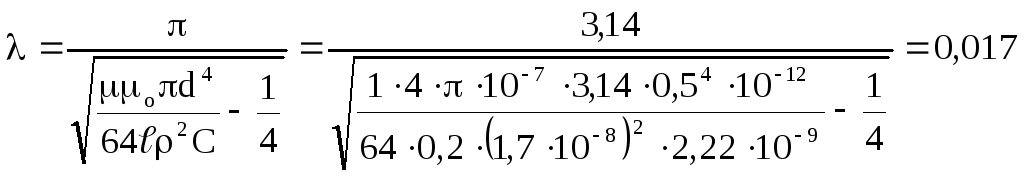Задача 3. Коливальний контур складається із конденсатора ємністю С = 0,2 мкФ і котушки індуктивністю L = 5 мГн. За час Δt = 1 мс амплітуда напруги на конденсаторі зменшилась у k = 3 рази. Знайти активний опір контуру R та логарифмічний декремент згасання λ.

Розв’язок. При згасаючих коливаннях амплітуда напруги на конденсаторі зменшується з часом по експоненті . Через час Δt амплітуда стане . За умовою задачі відношення цих напруг дорівнює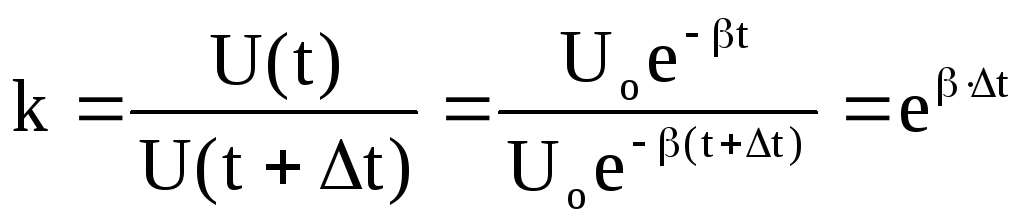. Знаходимо коефіцієнт згасання, який виражається через параметри контуру. Отже,.

Логарифмічний декремент Задача 4. Математичний маятник довжиною ℓ = 24,7 см здійснює згасаючі коливання з логарифмічним коефіцієнтом згасання λ = 0,2. Через який час Δt енергія коливань маятника зменшиться в k = 9,4 рази?

Розв’язок. Енергія коливань пропорційна квадрату амплітуди, яка з часом зменшується по експоненті . Тому відношення енергій. Знаходимо час. Логарифмічний декремент

. Знаходимо коефіцієнт згасання . Підставляємо у вираз часу

.

Задача 5. По ґрунтовій дорозі проїхав трактор, залишивши сліди у вигляді заглибин, які віддалені одна від другої на відстань ℓ = 0,3 м. по дорозі покотили дитячу коляску, пружини якої прогинаються на Δх = 2 см під дією навантаження F = 20 Н. Маса коляски з дитиною m = 10 кг. При якій швидкості V коляски потрапить у резонанс?

Розв’язок. Коляску будемо розглядати як пружинний маятник масою m з жорсткістю пружини . Оскільки про параметри згасання коливань нічого невідомо, будемо вважати, що резонансна частота коливань дорівнює частоті власних незгасаючих коливань. Небезпечна швидкість.