6. Приклади розв’язку задач

Задача 1. Точка здійснює гармонічне коливання з початковою фазою φ=0, періодом Т=2 с і амплітудою х_о= 50 мм. Знайти швидкість точки в момент часу, коли її зміщення від положення рівноваги дорівнює х₁= 25 мм.

Розв’язок. Рівняння гармонічного коливання має вид

, а закон зміни швидкості . В момент часу ,. Із першого рівняння знаходимо. Тоді швидкість

Задача 2. Амплітуда гармонічного коливання матеріальної точки х_о=2 см, а повна енергія коливань W = 3∙10^-7 Дж. При якому зміщенні х від положення рівноваги на точку буде діяти сила F = 2,25∙10^-5 Н?

Розв’язок. Рівняння гармонічного коливання має вид . За другим законом Ньютона сила. Енергія гармонічного коливання. Звідки знаходимоі підставляємо у вираз для сили. Одержуємо

Задача 3. Знайти амплітуду і початкову фазу гармонічного коливання, одержаного від складання однаково напрямлених коливань, які задані рівняннями м ім.

Розв’язок. На комплексній полині xoy зобразимо кожне коливання вектором, довжина якого дорівнює амплітуді, а початкове положення задається початковою фазою, відрахованою від осі ох проти годинникової стрілки. Амплітуду х_о одержаного коливання знаходимо за теоремою косинусів

Початкова фаза, згідно з виразом ( 9.22 )

Рівняння результуючого коливання буде мати вид

Задача 4. Точка одночасно приймає участь у двох взаємно-перпендикулярних коливаннях і. Знайти траєкторію результуючого руху точки та намалювати її.

Розв’язок. Для знаходження траєкторії руху необхідно у заданих рівняннях вилучити час t, тобто встановити зв’язок між x і y. Спочатку приведемо гармонічні функції до одного аргументу, скориставшись формулою косинуса подвійного кута

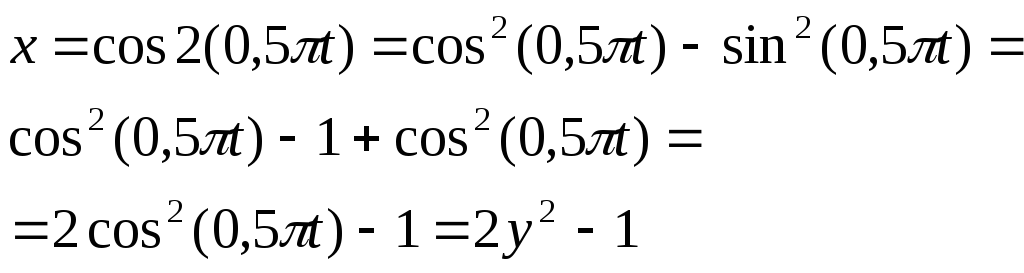
Графік функції є парабола. Точка рухається по її частині АВ, так як координата х згідно з умовою задачі не перевищує 1.

Задача5. Котушка індуктивністю L = 2,26∙10^-2 гн і активний опір R увімкнені у коло змінного струму частотою f = 50 Гц. Знайти величину опору R, якщо відомо, що зсув фаз між напругою і струмом φ = 60^о.

Розв’язок. Побудуємо векторну діаграму струмів і напруги. Побудову діаграми починаємо із загального параметру для всіх елементів – напруги. Відносно вектора напруги відкладаємо вектори струмів, взявши до уваги, що на активному опорі струм I_R співпадає по фазі з напругою, а на котушці струм I_L відстає від напруги U на 90^о. Із діаграми видно, що . Струми знайдемо за законом Ома,. Одержуємо

Задача 6. Конденсатор і електрична лампа з’єднані послідовної увімкнуті в коло змінного струму напругою U = 440 В і частотою f = 50 Гц. Яку електроємність С повинен мати конденсатор, щоб через лампу протікав струм І = 0,5 А і падіння напруги на лампі U_R =110 В?

Розв’язок. Побудуємо векторну діаграму струму і напруг, починаючи із загального параметру – струму. Відносно вектора струму будуємо вектори напруг, взявши до уваги, що на активному опорі (на лампі) напруга U_R співпадає по фазі з струмом I, а на конденсаторі напруга U_С відстає від струму I на 90^о. За законом Ома для дільниці кола

. Напруга U_С на конденсаторі, як показує векторна діаграма, знаходиться за теоремою Піфагора , а не просто як різниця. Таким чином одержуємо