2. Розподіл енергії в спектрі абсолютно чорного тіла. Формули Віна, Релея-Джинса, Планка

Для вивчення випромінювання різних тіл необхідно спочатку вивчити випромінювання абсолютно чорного тіла і перш за все його спектральну густину випромінювання U_λT, а потім скористатися законами Кіргхофа (13.8) чи (13.9).

Перші спроби теоретичного обгрунтування розподілу енергії в спектрі абсолютно чорного тіла зробив нім. фізик В.Він (1864-1928), який у 1893 р. знайшов аналітичний вид функції, яка носить його ім.’я

, (13.10)

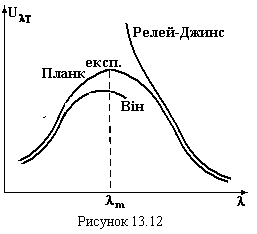
де а, b – константи. Вона справедлива лише для лівої частини експериментальної кривої (рис.13.12), тобто для малих довжин хвиль.

У 1900 р. англ. фізики Дж.Релей (1842-1919) і Д.Джинс виходячи із класичних уявлень про рівномірний розподіл енергії по степеням вільності одержали вираз

, (13.11)

де с - швидкість світла, k – стала Больцмана. Ця формула Релея-Джинса добре узгоджується з експериментальною кривою в інтервалі довгих хвиль (рис.13.12). Але вона приводить до абсурдного результату в області коротких довжин хвиль (ультрафіолетова область), де випромінювальна здатність абсолютно чорного тіла зростає до нескінченності. Це протиріччя одержало у фізиці назву “ультрафіолетової катастрофи”.

Для усунення цих протиріч нім. фізик М.Планк (1858-1947) висунув гіпотезу про квантовий характер випромінювання, тобто тіла випромінюють енергію не неперервно, а окремими порціями, які дістали назву квантів. Енергія кванта (13.12)

пропорційна частоті ν (обернено пропорційна довжині хвилі λ),

де h = 6,63∙10^-34 Дж∙с – стала Планка. Формула Планка (13.13)

дає узгодження з експериментальною кривою (рис. 13.12).

В граничних випадках формула Планка дає відповідно формулу Релея-Джинса при і формулу Віна при. Впевнимось у цьому.

При показник експоненти у (13) прямує до нуля і величинуможна розкласти в ряд, знехтувавши членами починаючи з третього, тому що вони набагато менші за перші два. Вираз (13) перетвориться у (11)

.

При показник експоненти у (1.313) прямує в нескінченність. Тому одиницею у знаменнику, порівнюючи з експонентою, можна знехтувати. Одержуємо формулу Віна

.

13.4 Закони випромінювання абсолютно чорного тіла: закон Стефана-Больцмана, закон Віна

Для інтегральної густини випромінювання абсолютно чорного тіла австрійські фізики Й.Стефан (1835-1893) у 1879 р. експериментально, а Л.Больцман (1844-1906) у 1884 теоретично сформулювали закон, який носить їхнє ім’я: інтегральна густина випромінювання абсолютно чорного тіла пропорційна четвертому степеню його абсолютної температури

, (13.14)

де – стала Стефана-Больцмана.

Одержимо цей закон виходячи з формули (13.13) Планка.

За формулою (13.7) .

Виконаємо заміни , а також врахуємо, що. Тому межі інтегрування зміняться місцями. Одержимо

.

Табличний інтеграл . Тому.

У 1893 р. В.Він встановив закон зміщення: довжина хвилі λ_m (рис.13.12), яка відповідає максимуму спектральної густини випромінювання абсолютно чорного тіла обернено пропорційна абсолютній температурі , (13.15)

де - стала Віна. При збільшенні температури максимум випромінювання зміщується в бік коротких хвиль.

Формула Планка (13.13) дає можливість теоретично одержати закон Віна. Для цього необхідно дослідити функцію планка на екстремум. Для цього беремо похідну по λ і прирівнюємо її нулю.

Маємо трансцендентне рівняння . Це рівняння має очевидний корінь х = 0. Але є іще один корінь , який лежить в інтервалі від 4 до 5, тому що ліва частина цього рівняння на цьому інтервалі змінює знак. Дійсно, при х = 4,

а при х = 5 Чисельним методом був знайдений корінь при х = 4,965. Отже,