Задача 3

Проведено вибірково обстеження (5% - не) сімей за сукупним доходом на 1 члена сім'ї і одержані дані (табл. 2.11).

Таблиця 2.11 - Дані про сукупний дохід сімей

Групи сімей за сукупним доходом на 1 члена сім'ї, грн.	Кількість сімей
До 40,0	12
40,0-60,0	10
60,0-80,0	19
80,0-100,0	42
100,0-120,0	12
120,0-140,0	3
140,0 і більше	2
Разом	100

Визначити:

1) середню суму сукупного доходу на 1 члена сім'ї, моду, медіану, показники варіації. Поясніть зміст одержаних характеристик;

2) з точністю 99,7% - граничну похибку вибірки та інтервал, в якому знаходиться сукупний доход у середньому на одного члена сім'ї;

3) з точністю 94,5% - граничну похибку вибіркової частки та можливі межі, де очікується частка ознаки в генеральній сукупності для модального інтервалу.

Розв'язання

1) Середня величина статистичної та середнє квадратичне відхилення сукупності обчислюються за формулами:

Для зручності обчислення складемо розрахункову таблицю 3.1. Тут середина інтервалу.

Мода — це значення випадкової величини, що трапляється найчастіше в сукупності спостережень. В інтервальному ряду конкретне модальне значення в середині інтервалу обчислюється за інтерполяційною формулою

де х₀ та h — відповідно нижня межа та ширина модального інтервалу,

—частоти (частки) відповідно модального, передмодального та післямодального інтервалів.

У даному випадку модальним інтервалом є інтервал 80-100 грн. Виходячи з цього обчислимо значення моди:

Таблиця 3.1. Розрахунки середньої величини і середнє квадратичного

відхилення

Групи сімей за сукупним доходом на 1 члена сім'ї, грн.	Середина інтервалу,	Кількість сімей,
До 40	30	12	360	-49,8	29760,48
40-60	50	10	500	-29,8	8880,40
60-80	70	19	1330	-9,8	1824,76
80-100	90	42	3780	10,2	4369,68
100-120	110	12	1320	30,2	10944,48
120-140	130	3	390	50,2	7560,12
140 і більше	150	2	300	70,2	9856,08
Разом		100	7980		73196,00

Медіана — значення ознаки, яке припадає на середину впорядкованого ряду, поділяє його навпіл — на дві рівні за обсягом частини. Для знаходження медіанного інтервалу розрахуємо кумулятивні (накопичені) частоти.

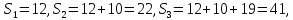
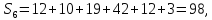
У даному випадку медіанним інтервалом є інтервал 80-100 грн. (для

цього інтервалу )=50.

В інтервальному ряду визначають медіанний інтервал, а значення медіани в середині інтервалу, як і значення моди, обчислюють за інтерполяційною формулою:

де х₀ та h — відповідно нижня межа та ширина медіанного інтервалу; — частота медіанного інтервалу; — кумулятивна частота передмедіанного інтервалу.

Виходячи з цього обчислимо значення медіани:

Знайдемо коефіцієнт варіації

Висновки:

• найчастіше в сукупності спостережень трапляється група сімей з сукупним доходом на 1 члена сім'ї в розмірі 89 грн.;

• половина сімей одержують сукупний дохід на 1 члена сім'ї у розмірі менше 84 грн., а друга – більше 84 грн.;

• оскільки =33,7% мало відрізняється від критичного значення коефіцієнта варіації (33,3%), то досліджувана сукупність однорідна, а розрахункова середня величина є типовою узагальнюючою характеристикою сукупності.

2) Різниця між показниками вибіркової і генеральної сукупності називається помилкою вибірки.

Оскільки вибіркова середня і вибіркова частка є випадковими величинами, то помилки вибірки також є випадковими величинами і можуть приймати різні значення. Тому визначають середню з можливих помилок (μ).

n — об'єм вибіркової сукупності (n=100 од.);

N - об'єм генеральної сукупності (N=100/0,05=2000од.);

—загальна дисперсія.

Для вирішення практичних завдань крім середньої користуються граничної помилкою вибірки, яка пов'язана з рівнем імовірності, що гарантує її. Рівень ймовірності визначає величина нормованого відхилення t, і навпаки. Значення t для ймовірності 0,997 дорівнює 3. Отже, визначаємо граничну похибку:

Таким чином інтервал можливих значень середнього розміру результативної ознаки для генеральної сукупності :

Обчислюємо

Висновок:

• з ймовірністю 0,997 можна стверджувати, що сукупний дохід на 1 члена сім'ї в генеральній сукупності знаходиться в межах від 71,9 до 87,7 грн..

3) Гранична помилка частки знаходиться за формулою:

де частки групи одиниць модального інтервалу в вибіркової сукупності.

Знайдемо:

Значення t для ймовірності 0,954 дорівнює 2.Маємо:

Інтервал можливих значень частки одиниць модального інтервалу для генеральної сукупності p:

Обчислюємо

Висновок:

з ймовірністю 0,954 можна стверджувати, що частка одиниць модального інтервалу в генеральній сукупності знаходиться в межах від 32,4% до 51,6%.