5. Формулы Бейеса.

Формулы Бейеса применяются при решении практических задач, когда событие , появляющееся совместно с каким-либо из событий , , … , , которые образуют полную группу несовместимых событий, произошло и требуется произвести количественную переоценку вероятностей событий , , … , . Априорные (до опыта) вероятности , , … , известны. Требуется вычислить апостериорные (после опыта) вероятности, т. е. по существу нужно найти условные вероятности , , … ,. Для события формула Бейеса выглядит так:

.

Раскрывая в этом равенстве по формуле полной вероятности (2.1), имеем:

.

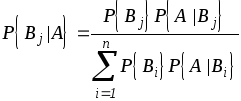Пример 8. Пользуясь данными примера 7, рассчитать вероятности того, что в сборку попала деталь, изготовленная на первом, втором и третьем станках соответственно, если узел сходящий с конвейера, годный.

Решение. Расчет условных вероятностей произведем по формуле Бейеса. Имеем:

для первого станка

;

для второго станка

;

для третьего станка

.

ЗАДАЧИ

1. Бросили монету и игральную кость. Определить, зависимы или независимы события: - выпал “герб”; - выпало четное число очков.

Ответ: независимы.

2. Брошены последовательно три монеты. Определить, зависимы или независимы события: - выпадение “герба” на первой монете; - выпадение хотя бы одной “решетки”.

Ответ: зависимы.

3. Бросили игральную кость. Какова вероятность того, что выпало простое число очков, если известно, что число выпавших очков нечетно ?

Ответ: 2/3.

4. В ящике лежат красных, зеленых и синих шаров. Наудачу вынимается два шара. Какова вероятность, что извлечены шары разного цвета, если известно, что не извлечен синий шар ?

Ответ: 48/95.

5. В одном ящике белых и красных шаров, в другом ящике белых и красных шаров. Найти вероятность того, что хотя бы из одного ящика будет извлечен один белый шар, если из каждого ящика извлечено по одному шару.

Ответ: 7/9.

6. Вероятность того, что в течение одной смены возникнет неполадка станка, равна . Какова вероятность того, что не произойдет ни одной неполадки за три смены ?

Ответ: (0,95)³=0,857375.

7. В ящике красных и синих пуговиц. Вынимаются наудачу две пуговицы. Какова вероятность того, что пуговицы будут одноцветными ?

Ответ: 0,5.

8. Найти вероятность того, что наудачу взятое двузначное число окажется кратным , либо , либо тому и другому одновременно.

Ответ: 0,6.

9. Студент пришел на зачет, зная из вопросов только . Какова вероятность сдать зачет, если после отказа отвечать на вопрос преподаватель задает еще один вопрос ?

Ответ: 28/29.

10. Имеется два одинаковых ящика с шарами. В первом ящике белых и черный шар, во втором - белый и черных шара. Наудачу выбирают один ящик и извлекают из него шар. Какова вероятность, что извлеченный шар окажется белым ?

Ответ: 13/30.

11. В цехе работают станков. Из них марки , марки и марки . Вероятность того, что качество деталей окажется отличным, для этих станков соответственно равна: , и . Какой процент отличных деталей выпускает цех в целом ?

Ответ: 83%.

12. Студент знает не все экзаменационные билеты. В каком случае вероятность вытащить неизвестный билет будет для него наименьшей, когда он тащит билет первым или последним ?

Ответ: безразлично.

13. На фабрике, изготовляющей болты, первая машина производит %, вторая - %, третья - % всех изделий. В их продукции брак составляет соответственно %, % и %.

а) Какова вероятность того, что случайно выбранный болт дефектный ?

б) Случайно выбранный из продукции болт оказался дефектным. Какова вероятность того, что он был произведен первой, второй, третьей машиной ?

Ответ: а) 0,0345; б) 125/345, 140/345, 80/345.