У режимі модуляції потужність безупинно змінюється. Її

максимальне і мінімальне значення визначаються вираженнями:

. (7.1.8)

Потужність двох бічних частот (при модуляції чистим тоном) і _o>>б дорівнює

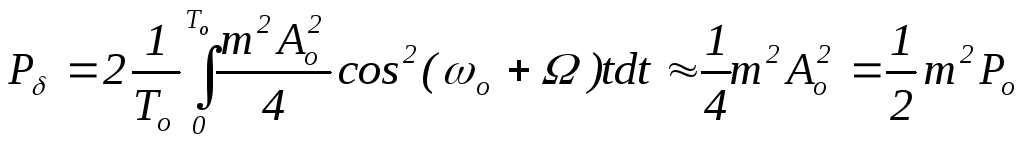. (7.1.9)

Середня за період модуляції потужність буде дорівнювати

, (7.1.10)

де - період коливання, що модулює.

З останніх виражень при m=1 одержимо

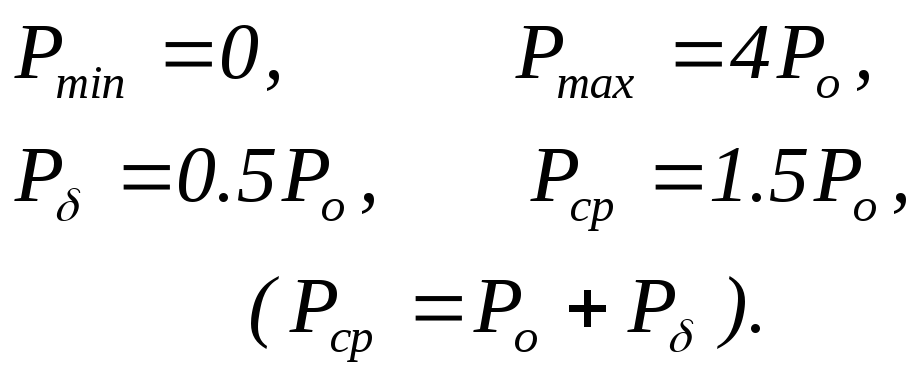(7.1.11)

Таким чином, при стовідсотковій модуляції 2/3 усієї потужності витрачається на передачу несучого коливання і 1/3 – на передачу бічних частот. Обумовлене модуляцією збільшення потужності, що в основному і визначає умови виділення повідомлення при прийомі, у цьому випадку не перевищує половини потужності несучого коливання. Крім того, велика величина пікової потужності в порівнянні із середньою вимагає лінійного режиму роботи тракту прийому-передачі в широкому динамічному діапазоні (підсилювальні елементи повинні вибиратися по максимальній потужності). Сказане дозволяє укласти, що амплітудна модуляція з енергетичної точки зору має істотні недоліки.

Зазначені недоліки амплітудної модуляції можна значною мірою усунути, якщо використовувати передачу з подавленою несучою. Придушення несучої здійснюється при використанні балансової амплітудної модуляції (БАМ). Цей вид модуляції називають ще двухполосной модуляцією (ДМ).

При балансовій модуляції сигнал записується у виді

, (7.1.12)

відкіля при модуляції чистим тоном одержимо

(7.1.13)

тобто тільки дві бічні частоти без несучої. На мал.7.1.6 показан спектр сигналу при балансовій модуляції і тимчасові діаграми при звичайній і балансовій амплітудній модуляції. Тимчасова діаграма в останньому випадку виходить шляхом вирахування зі звичайного

Р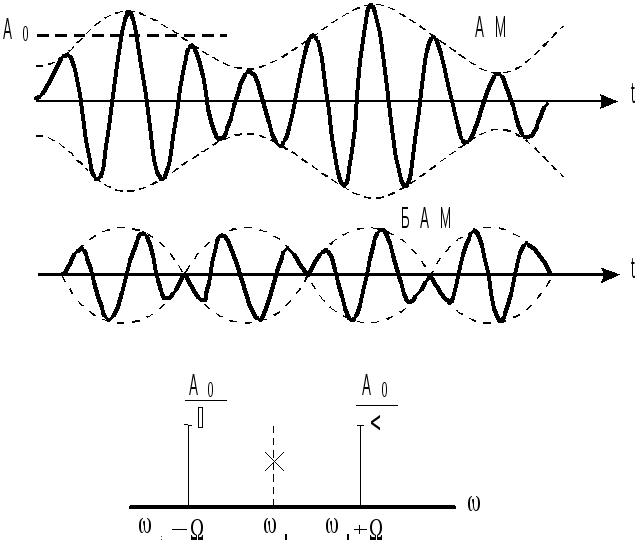ис. 7.1.6.

АМ коливання складової . Неважко бачити, що оги-бающая при балансовій модуляції має подвоєну частоту, а фаза високочастотного заповнення міняється стрибком на 180^про при кожнім переході обгинає через нульове значення. Дуже показовим прикладом цього може служити амплітудно-маніпульовані коливання з придушенням несучої (малий.7.1.7). Таке АМн коливання по су-

Р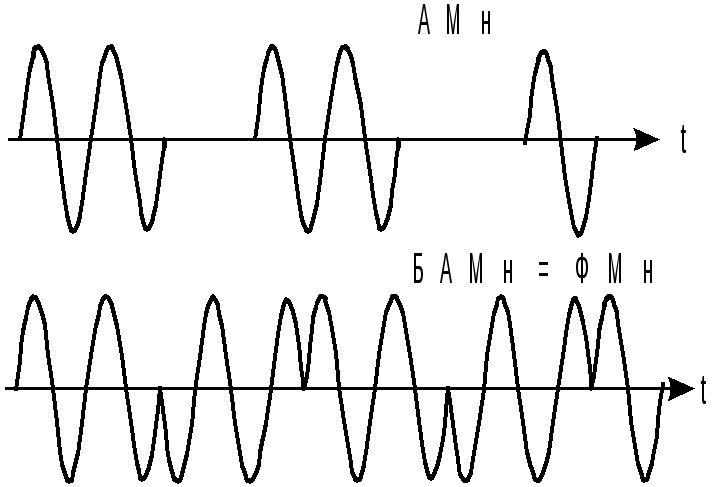ис. 7.1.7.

ті є фазо-маніпульованим коливанням, що буде розглянуто докладніше нижче . Однак вже зараз можна відзначити, що фазо-маніпульоване коливання буде мати амплітудний спектр Амн коливання з подавленої несучий.

Ще одним різновидом АМ є однополосна модуляція ( чиОМ ОБП), при якій передається тільки одна бічна смуга частот. При модуляції чистим тоном у цьому випадку з (7.1.13) маємо

. (7.1.14)

Використання БАМ і ОМ дозволяє скоротити марну витрату енергії на складову несучої частоти, а при ОМ - скоротити додатково вдвічі ширину спектра переданого сигналу. Однак для демодуляції сигналу на прийомній стороні несуча необхідна. Необхідність відновлення несучої вимагає деякого ускладнення схеми прийому.

7.2 Частотна модуляція

При частотній модуляції за законом коливання, що модулює, U(t) змінюється частота високочастотного несучого коливання.

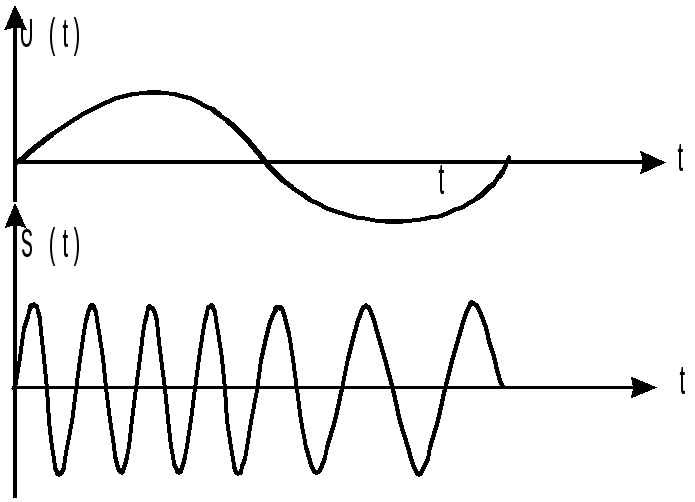
На мал.7.2.1 показані графіки що модулює і модульованого сигналів у випадку модуляції чистим тоном. Одержимо аналітичне вираження для Чм-коливання. При модуляції чистим тоном

Рис. 7.2.1.

, (7.2.1)

де - максимальне відхилення частоти, називане девіацією частоти, а- відносна зміна частоти. По своєму визначенню миттєва кругова частота є похідної за годиною від аргументу тригонометричної функції cos(t), що представляє коливання, тобто

. (7.2.2)

З останнього вираження одержимо

, (7.2.3)

тобто фаза коливання визначається інтегралом від кругової частоти. Тому для ЧМ - коливання при модуляції чистим тоном можна записати

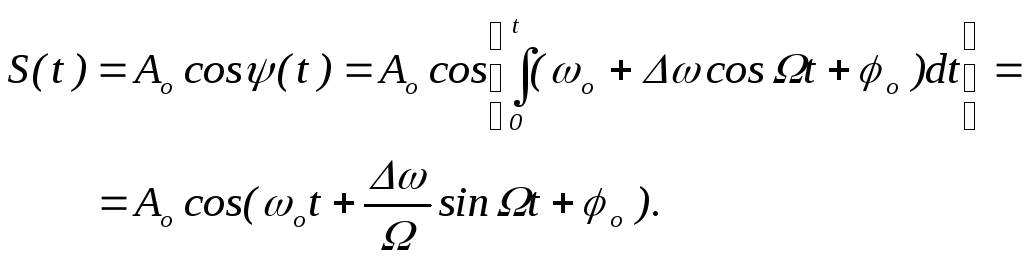(7.2.4)

Зауважуємо, що зміна частоти за законом приводить до зміни фази за законом. Величинаназивається індексом частотної модуляції і має сенс максимальної величини (амплітуди) зміни фази при частотній модуляції.

Заміняючи косинус суми двох кутів по відомих формулах тригонометрії, замість (7.2.4) при одержимо

. (7.2.5)

Визначимо тепер спектр частотно-модульованого сигналу. Почнемо з випадку малого індексу модуляції, коли . У цьому випадку

(7.2.6)

. (7.2.7)

Зауважуємо, що при малому індексі модуляції спектр ЧМ - коливання відрізняється від спектра АМ - коливання тільки зрушенням фази нижньої бічної частоти на 180^о. Це ілюструється мал.7.2.2, на якому показана векторна діаграма для ЧМ - коливання (порівняй з мал.7.1.3).

Н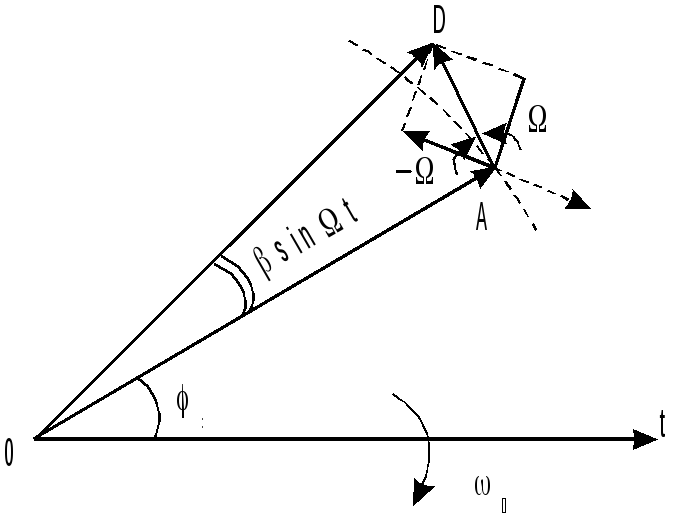а діаграмі результуючий вектор ОД змінюється як по фазі, так і по амплітуді,однак приамплітудні зміни настільки малі, що ними можна зневажити. При довільних значеннях  с обліком усіх частотних складових спектра результуючий вектор буде змінюватися тільки по фазі.

Визначимо тепер спектр ЧМ - коливання при довільному індексі модуляції. Для цього періодичні функції ірозкладемо у виряджай Фур'є, коефіцієнти яких, як доводитися в теорії бесселевих функцій, є функціями Бесселя першого роду:

, (7.2.8)

. (7.2.9)

Підставляючи останні вираження в (7.2.5) і роблячи тригонометричні перетворення, остаточно одержимо

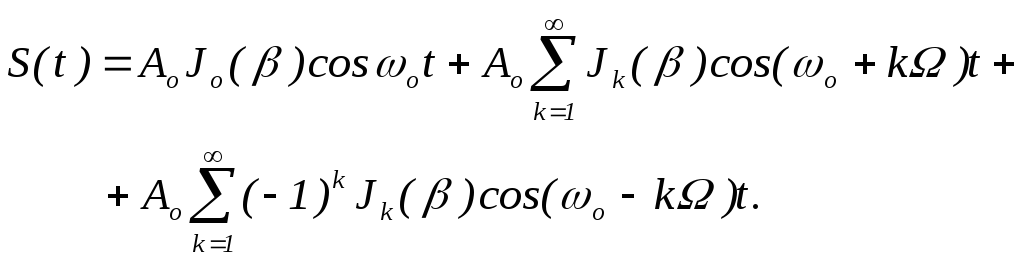(7.2.10)

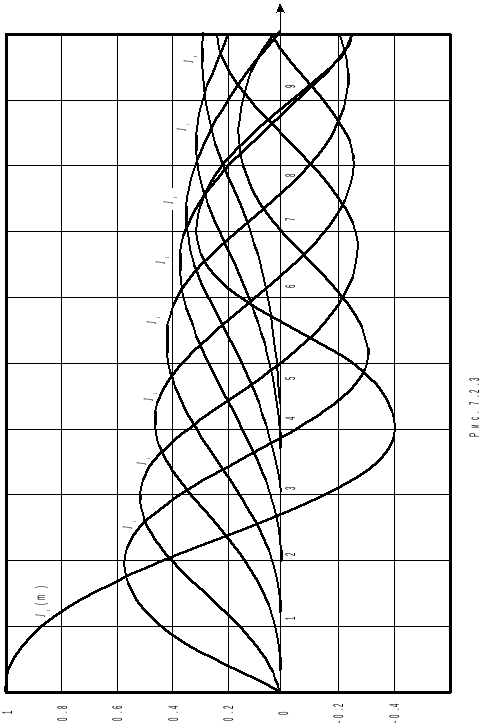
Таким чином, ЧМ коливання при модуляції чистим тоном має дискретний спектр і складається з несучої і нескінченного числа бічних частот з амплітудами. Однак практично ширина спектра при частотній модуляції обмежена. Це можна помітити на мал.7.2.3, на якому приведені графіки функцій. Приіфункціїубувають настільки швидко, що ними можна зневажити, тобто вважати, що. Тому ширина спектра при широкополосній ЧМ () буде дорівнює

, (7.2.11)

тобто приблизно дорівнює подвоєної девіації частоти.

Р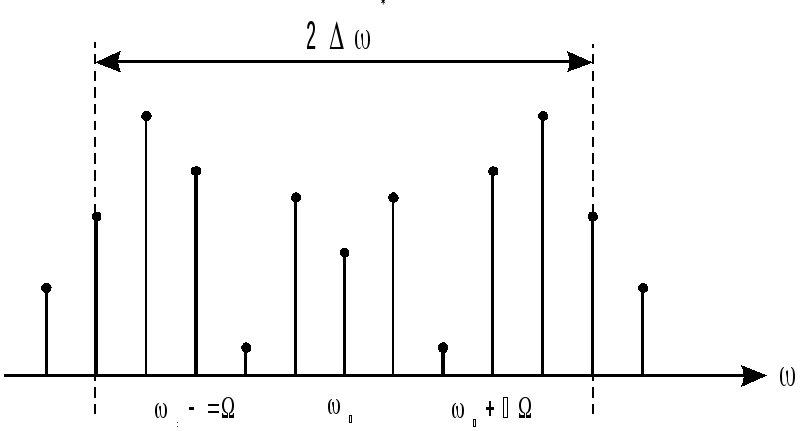ис. 7.2.4.

На мал.7.2.4 як приклад показань графік модуля спектра ЧМ коливання при = 5.

Таким чином, ширина спектра при широкополосній ЧМ у +1 раз ширше, ніж звичайної АМ. Перевагою частотної модуляції є сталість потужності, тому що амплітуда сигналу в процесі модуляції не змінюється.

Відзначимо тепер, що при частотній модуляції девіації частоти визначається амплітудою сигналу, щомодулює, U(t). При зменшенні амплітуди сигналу, що модулює, зменшується індекс модуляції і дійсна ширинаспектра . При постійній амплітуді і зміна частоти моделюючого сигналу змінює індекс модуляції, число ліній і інтервал між лініями в спектрі ЧМ коливання, однак ширина спектрапрактично залишається постійної.

Вище розглядався випадок модуляції чистим тоном. При модуляції складним сигналом спектр ЧМ коливання буде більш богатим, а ширина спектра при буде дорівнює

, (7.2.12)

де - максимальна кругова частота в спектрі сигналу, що модулює.