2.3 Задачі до практичної частини

Завдання 1

На машинобудівному підприємстві передбачається випуск 3-х видів верстатів Ι, ІΙ, ІΙІ. При цьому витрачається сировина, трудові ресурси та накладні витрати.

Для виготовлення верстату Ι – го виду потрібно 4 од. сировини, 2 од. трудових ресурсів та 10 од. накладних витрат; верстату ΙІ – го виду 6 од. сировини, 2 од. трудових ресурсів та 8 од. накладних витрат; для верстату ΙΙІ – го виду потрібно 4 од. сировини, 2 од. трудових ресурсів та 18 од. накладних витрат; Підприємство має у наявності 420 од. сировини, 120 од. трудових ресурсів та 250 од. накладних витрат.

Прибуток від реалізації станка І виду - 28 тис. грн., ІΙ виду - 24 тис. грн., ΙІΙ виду - 20 тис. грн. За умовами виробництва потрібно, щоб трудові ресурси були використані повністю, а накладні витрати не перевищували встановленого рівня.

Створити модель для пошуку плану виробництва верстатів, який забезпечує максимальний прибуток і вирішити задачу.

Завдання 2

Фірма виготовляє три вида продукції (А, В, С), для випуску кожної потрібно час на чотирьох видах устаткування I, II, Ш, IV.

Вид продукції	Час оброрбки, (г.)				Прибуток, долл.
	I	И	III	IV
А	1	3	1	2	3
В	6	1	3	3	6
С	3	3	2	4	4

Резерв фонду робочого часу устаткування відповідно складає 84, 42, 21 и 42 години. Визначте, яку продукцію і в якої кількості варто виготовляти щоб прибуток був максимальний. (Ринок збуту для кожного продукту необмежений).

Скласти модель і вирішити задачу.

Завдання 3

На машинобудівному підприємстві за умовами зовнішньоекономічного контракту передбачається випуск 3-х видів верстатів Ι, ІΙ, ІΙІ. При цьому витрачається сировина, трудові ресурси та накладні витрати. Для виготовлення верстату Ι – го виду потрібно 4 од. сировини, 2 од. трудових ресурсів та 10 од. накладних витрат; верстату ΙІ – го виду 6 од. сировини, 2 од. трудових ресурсів та 8 од. накладних витрат; для верстату ΙΙІ – го виду потрібно 4 од. сировини, 2 од. трудових ресурсів та 18 од. накладних витрат; Підприємство має у наявності 420 од. сировини, 120 од. трудових ресурсів та 250 од. накладних витрат. Прибуток від реалізації станка І виду - 28 тис. грн., ІΙ виду - 24 тис. грн., ΙІΙ виду - 20 тис. грн. За умовами виробництва потрібно, щоб трудові ресурси були використані повністю, а накладні витрати не перевищували встановленого рівня.

Створити модель для пошуку плану виробництва верстатів, який забезпечує максимальний прибуток і вирішити задачу.

Завдання 4

В міжнародному дитячому таборі, який організовано для вивчення іноземних мов, треба організувати ефективне харчування. Продовж відпочинку кожна дитина повинна щодня отримувати не менше од. речовини,од. речовини,од. речовини(речовиниможуть, наприклад означати: жири, вуглеводи, білки). Для годування дітей можна закупити три основні види продуктів: I, II, III (наприклад: картопля, м’ясо, молоко). Місткість кожної речовини в різних видах продуктів і вартість одиниці кожного продукту наведена в таблиці 2.1.

Поживні речовини	Норма (мін. добова потреба)	Види продуктів
		I	II	III
A	8	1	8	3
B	12	8	1	6
C	6	2	10	2
Вартість		2	12	4

Потрібно забезпечити найбільш дешевий і повноцінний раціон. Скласти економіко-математичну модель і вирішити задачу.

Завдання 5

За умовами зовнішньоекономічного контракту ведеться підготовка до випуску двох видів костюмів - чоловічих і жіночих. На жіночий костюм потрібно 1 м вовни, 2 м лавсанової тканини й 1 людино-день витрат трудових ресурсів, на чоловічий костюм - 3,5 м вовни, 0,5 м лавсану й 1 людино-день витрат трудових ресурсів. Усього є 350 м вовни, 240 м лавсану й 150 людино-днів трудових ресурсів. За планом передбачається випуск не менш 110 костюмів, причому необхідно забезпечити прибуток не менш 10 тис. евро. Потрібно забезпечити оптимальну кількість костюмів кожного виду для досягнення максимального прибутку, якщо прибуток від реалізації жіночого костюма становить 70 евро, а від реалізації чоловічого – 50 евро.

Скласти економіко-математичну модель і вирішити задачу.

Завдання 6

Деталі № 1 і № 2 можна виготовити на верстатах А и В. Продуктивність верстатів (у хвилину) при виробництві деталей наведена в таблиці:

Деталі Верстати	№ 1	№ 2
А В	4 1	2 6

У комплект входять одна деталь № 1 і дві деталі № 2. Потрібно виготовити за зміну найбільшу кількість комплектів. Фонд робочого часу кожного верстата шість годин. Складіть математичну модель даного завдання і вирішити задачу

Завдання 7

У ресторані готуються фірмові блюда трьох видів (блюдо A, блюдо B і блюдо C) з використанням при готуванні інгредієнтів трьох видів (інгредієнт 1, інгредієнт 2 і інгредієнт 3). Видаток інгредієнтів у грамах на блюдо задається наступною таблицею:

Вид інгредієнта	Блюдо A	Блюдо B	Блюдо C
Інгредієнт 1	20	50	10
Інгредієнт 2	20	0	40
Інгредієнт 3	20	10	10

Вартість готування блюд однакова (20 грн.). Щодня в ресторан надходить 5 кг інгредієнта 1 і по 4 кг інгредієнтів 2 і 3. Яке оптимальне співвідношення денного виробництва блюд різного виду, якщо виробничі потужності ресторану дозволяють використовувати весь запас продуктів, що надійшли?

Скласти економіко-математичну модель і вирішити задачу.

Завдання 8

Для виготовлення виробів А и В використовується токарне, зварювальне й фрезерне встаткування. Витрати часу на обробку одного виробу для кожного з устаткування зазначені в таблиці. У ній же зазначений загальний фонд робочого часу кожного з типів використовуваного встаткування, а також прибуток від реалізації одного виробу кожного виду.

Назва встаткування	Витрати часу на обробку виробу		Загальний фонд робочого часу
	А	В
Фрезерне	3	1	75
Токарне	1	1	30
Зварювальне	1	4	84
Прибуток	3	4

Потрібно визначити, скільки виробів і якого виду варто виготовити підприємству, щоб прибуток був максимальним.

Скласти економіко-математичну модель і вирішити задачу.

Завдання 9

Фірма займається складанням дієти, що містить принаймні 20 одиниць білків, 30 одиниць вуглеводів, 10 одиниць жирів і 40 одиниць вітамінів. Як дешевше всього досягти цього при зазначених цінах (у гривнях) на 1 кг (або 1 л) п'яти наявних продуктів?

	Хліб	Соя	Сушена риба	Фрукти	Молоко
Білки	2	12	10	1	2
Вуглеводи	12	0	0	4	3
Жири	1	8	3	0	4
Вітаміни	2	2	4	6	2
Ціна	2	7	32	18	10

Скласти економіко-математичну модель і вирішити задачу.

Завдання 10

Фірма виготовляє два продукти А и В, ринок збуту яких необмежений. Кожний продукт повинен бути оброблений кожною машиною I, II, III. Час обробки в годинниках для кожного з продуктів А и В наведено нижче.

	I	II	III
А	0.5	0.4	0.2
В	0.25	0.3	0.4

Час роботи машин I, II, III відповідно 40, 36 і 36 годин на тиждень. Прибуток від виробів А и В становить відповідно 5 і 3 долари. Фірмі треба визначити тижневі норми випуску виробів А и В, які надають максимум прибутку. Скласти економіко-математичну модель і вирішити задачу.

Завдання 11

В дитячому таборі відпочинку кожна дитина повинна щодня отримувати не менше 8 од. речовини A, 12 од. речовини B, 6 од. Речовини C (речовини A,B,C можуть, наприклад означати: жири, вуглеводи, білки). Для годування дітей можна закупити три основні види продуктів: I, II, III (наприклад: картопля, м’ясо, молоко). Місткість кожної речовини в різних видах продуктів і вартість одиниці кожного продукту наведена в таблиці.

Поживні речовини	Норма (мін. добова потреба)	Види продуктів
		I	II	III
A	8	1	8	3
B	12	8	1	6
C	6	2	10	2
Вартість		2	12	4

Потрібно забезпечити найбільш дешевий і повноцінний раціон. Скласти економіко-математичну модель і вирішити задачу.

Завдання 12

Проведення рекламної компанії підприємство використовувало 4 джерела масової інформації:

Телебачення;

Радіо;

Газета;

Розклеювання об’яв.

Аналіз рекламної діяльності в попередньому періоді показав, що ці засоби доводять до збільшення прибутку відповідно на 10, 5,7 і 4 у.о. в розрахунку на 1 у.о. витрат на рекламу. Бюджет реклами заплановано в розмірі 50000 у.о. Адміністрація не має наміру витрачати на телебачення більш 40%, радіо і газети більш 50%.

Як запланувати рекламну компанію, щоб одержати максимальний прибуток? Скласти економіко-математичну модель і вирішити задачу.

Завдання 13

Привести до канонічного виду задачу лінійного програмування. Задача має вигляд:

Знайти Y = 2х₁+3х₂ → max

при обмеженнях:

х₁+3х₂ ≤ 18,

2х₁+х₂ ≤ 16,

х₂ ≤ 5,

3х₁ ≤ 21,

х₁ ≥ 0, х₂ ≥ 0.

Завдання 14

Привести до канонічного виду задачу лінійного програмування. Задача має вигляд:

Знайти Y = 2х₁ - х₂ → min

при обмеженнях:

 x₁ + x₂  1,

 2x₁ + 5x₂ ≤ 6,

 x₁  0 , x₂  0

Завдання 15

Привести до канонічного виду задачу лінійного програмування. Задача має вигляд:

Знайти F(x) = 3х₁+5х₂+4х₃  max

при обмеженнях:

 2х₁+3х₂≤8,

 2х₂+5х₃≤10,

 3х₁+2х₂+4х₃≤15.

x_j  0 ( j = 1, 2, 3)

Завдання 16

Привести до канонічного виду задачу лінійного програмування. Задача має вигляд:

Знайти F(x) = 2х₁+5х₂  max

при обмеженнях:

 -4х₁ + х₂ ≤ 1,

 -2х₁ + х₂ ≤ 3,

 2х₁ + х₂ ≤ 11,

 5х₁ + х₂ ≤ 20,

 х₁  0 х₂  0

Завдання 17

Привести до канонічного виду задачу лінійного програмування. Задача має вигляд:

Знайти F(x) = 5х₁ + 2х₂ - 3х₃ + х₄ max

при обмеженнях:

 2х₁ - х₂ + х₃ + х₄ ≤ 5,

 х₁ + х₂ - х₃ - х₄ ≤ 2,

 5х₁ - 8х₂ + 2х₃ + 4х₄ ≤ 3

х₁  0 х₂  0

Завдання 18

Привести до канонічного виду задачу лінійного програмування. Задача має вигляд:

Знайти F(x) = х₁ + 3х₂ + х₃  max

при обмеженнях:

 3х₁ + 2х₂ - х₃ ≤ 5,

 х₁ - 4х₂ - 2х₃ ≤ 3,

 2х₁ - 5х₂ + х₃ ≤ 2

х₁  0 х₂  0 х₃  0

Завдання 19

Привести до канонічного виду задачу лінійного програмування. Задача має вигляд:

Знайти F(x) = 3х₁ - 2х₂ - х₃ min

при обмеженнях:

 х₁ + х₂ + х₃ ≥ 5,

 21х₁ + 14х₂ + 6х₃ ≥ 42,

 2х₁ - 3х₂ + х₃ ≥ -6

 -х₁ - 2х₂ + х ₃ ≤ 4

х₁  0 х₂  0 х₃  0

Завдання 20

Привести до канонічного виду задачу лінійного програмування. Задача має вигляд:

Знайти F(x) = 3х₁ + 3х₂ + 4х₃ min

при обмеженнях:

 4х₁ + х₂ + 3х₃ ≥ 14,

 2х₁ + х₂ + х₃ ≥ 10,

 2х₁ + 2х₂ + 2х₃ ≥ 14

 х₁ + 3х₂ + х₃ ≥ 10

х₁  0 х₂  0 х₃  0

Завдання 21

Привести до канонічного виду задачу лінійного програмування. Задача має вигляд:

Знайти F(x) = х₁ + 2х₂  max

при обмеженнях:

 x₁ - x₂  3

 2x₁ - x₂ + 2  0

 x₁ + 3x₂  14

 x₂  4

 x₁  5

x_j  0 ( j = 1, 2)

Завдання 22

Привести до канонічного виду задачу лінійного програмування. Задача має вигляд:

Знайти F(x) = x₁ + x₂  max

при обмеженнях:

 x₁ + 2x₂ - 4  0

 2x₁ + x₂ - 4  0

 x₁ - x₂ + 4  0

 x₁ + 6x₂ - 6  0

 x₁  5

x_j  0 ( j = 1, 2)

Завдання 23

Привести до канонічного виду задачу лінійного програмування. Задача має вигляд:

Знайти Y = 2х₁+3х₂ → max

при обмеженнях:

х₁+3х₂ ≤ 18,

2х₁+х₂ ≤ 16,

х₂ ≤ 5,

3х₁ ≤ 21,

х₁ ≥ 0, х₂ ≥ 0.

Завдання 24

Привести до канонічного виду задачу лінійного програмування. Задача має вигляд:

Знайти Y = 2х₁ - х₂ → min

при обмеженнях:

 x₁ + x₂  1,

 2x₁ + 5x₂ ≤ 6,

 x₁  0 , x₂  0

Завдання 25

Побудувати двоїсту задачу до ЗЛП.

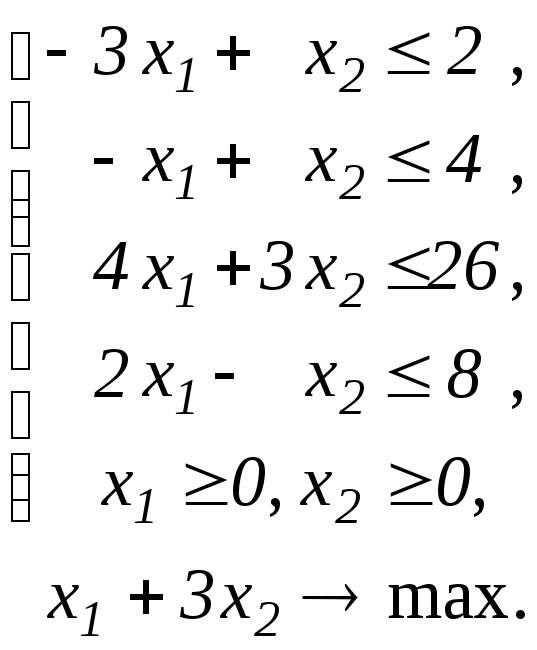
Завдання 26

Побудувати двоїсту задачу до ЗЛП.

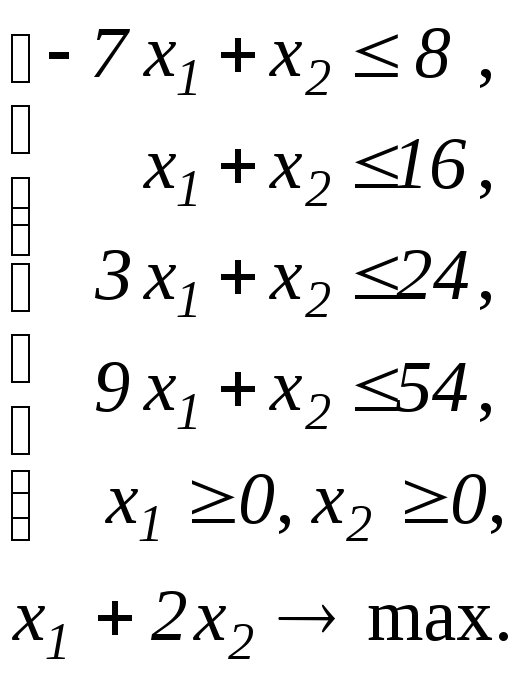
Завдання 27

Побудувати двоїсту задачу до ЗЛП.

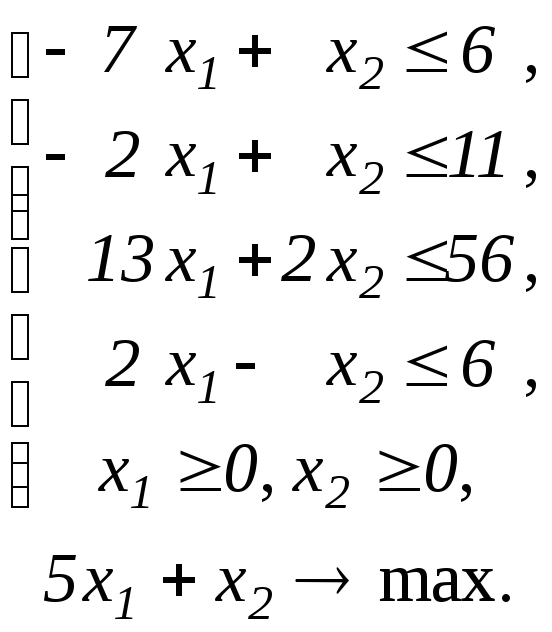
Завдання 28

Побудувати двоїсту задачу до ЗЛП.

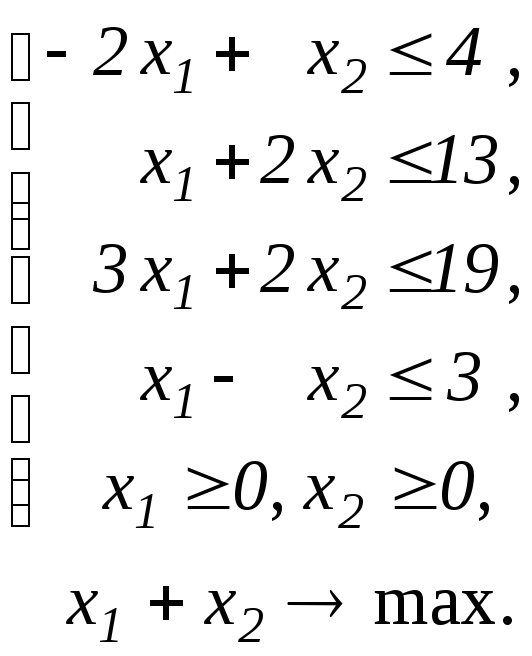
Завдання 29

Побудувати двоїсту задачу до ЗЛП.

Завдання 30

Побудувати двоїсту задачу до ЗЛП.

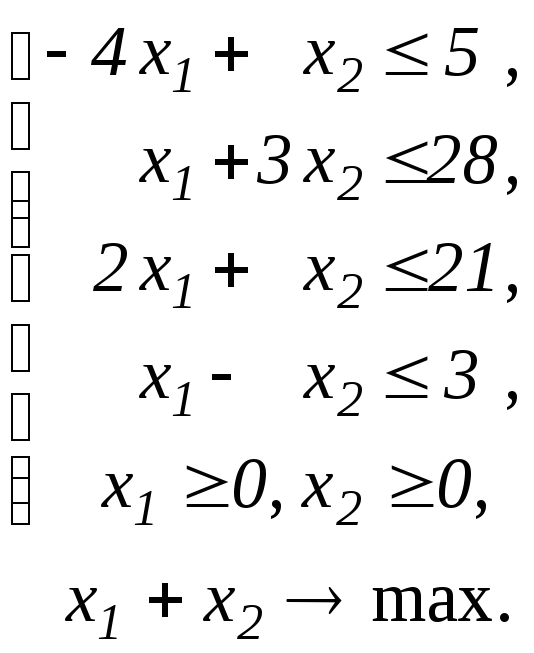
Завдання 31

Побудувати двоїсту задачу до ЗЛП.

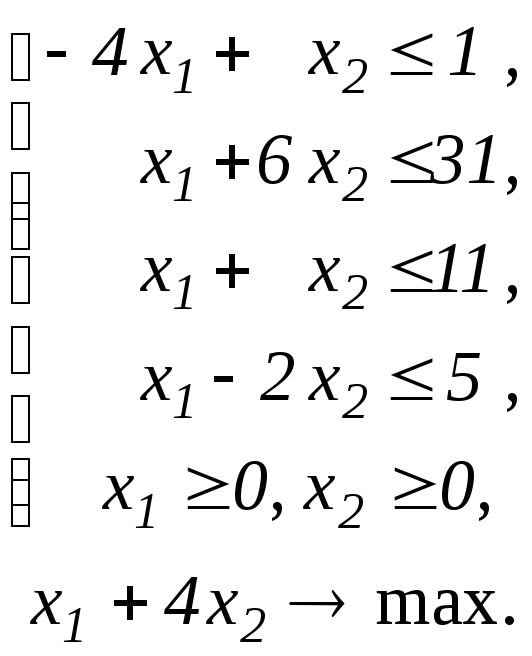
Завдання 32

Побудувати двоїсту задачу до ЗЛП.

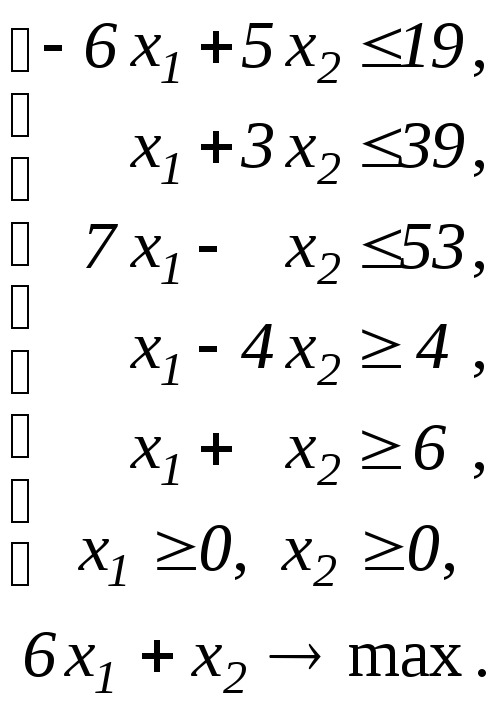
Завдання 33

Побудувати двоїсту задачу до ЗЛП.

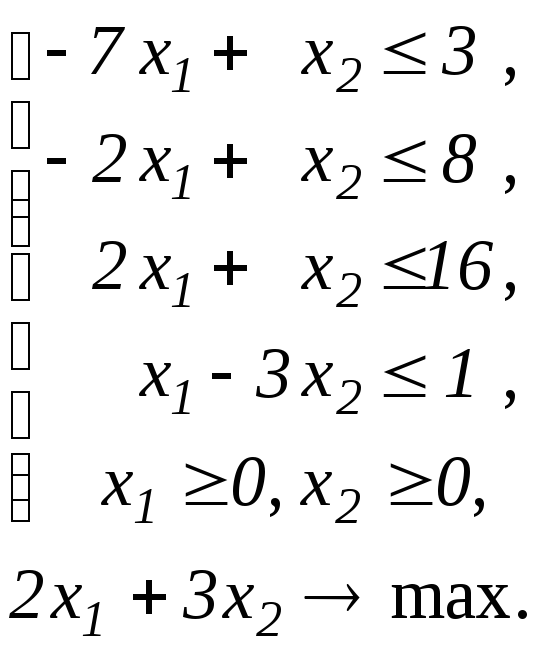
Завдання 34

Побудувати двоїсту задачу до ЗЛП.

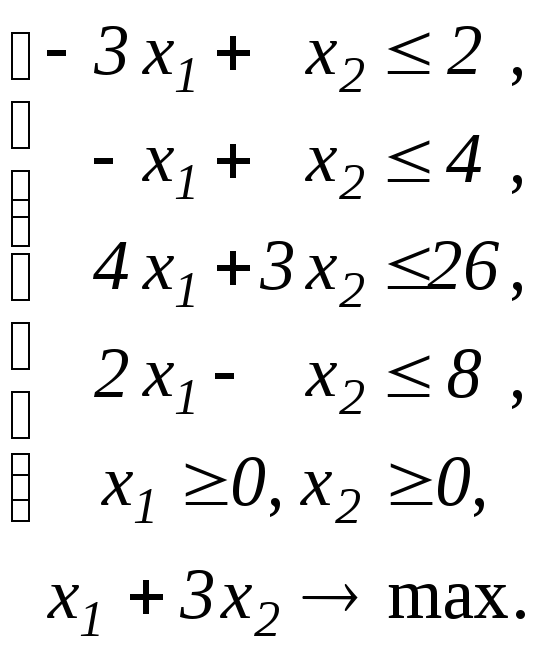
Завдання 35

Побудувати двоїсту задачу до ЗЛП.

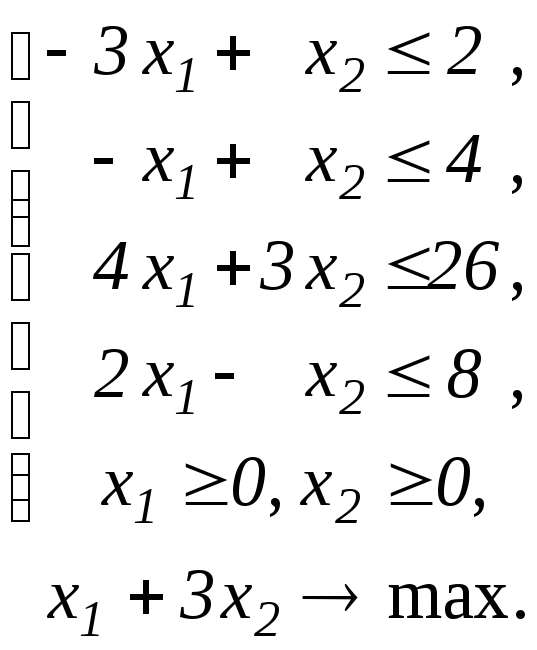
Завдання 36

Побудувати двоїсту задачу до ЗЛП.

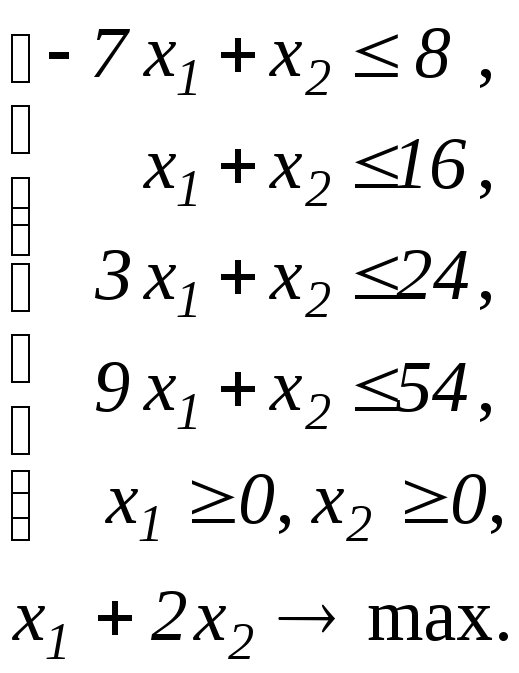
Завдання 37

Перевірити баланс. При необхідності привести до збалансованого вигляду за рахунок штучного введення постачальника a_i, або споживача b_jз вартістю виконання перевезень 10. Знайти первісний опорний план транспортної задачі за правилом „північно-західного кута”, та методом мінімального елементу. Розрахувати і порівняти результати. Розв’язати транспортну задачу за методом потенціалів.

	bj ai	120	75	145	65			bj ai	50	110	145	85
	115	1	8	2	1			165	3	2	4	1
	85	3	7	6	2			75	7	3	1	5
	80	5	3	5	4			130	6	2	5	4
	55	4	3	1	6
	70	5	7	8	2

Завдання 38

Перевірити баланс. При необхідності привести до збалансованого вигляду за рахунок штучного введення постачальника a_i, або споживача b_jз вартістю виконання перевезень 10. Знайти первісний опорний план транспортної задачі за правилом „північно-західного кута”, та методом мінімального елементу. Розрахувати і порівняти результати. Розв’язати транспортну задачу за методом потенціалів.

	bj ai	120	60	145	70			bj ai	80	140	65	30
	50	1	3	8	5			90	2	4	1	3
	90	4	1	2	7			130	1	6	5	4
	75	6	5	3	2			155	3	7	9	5
	80	3	4	8	1
	100	6	5	7	2

Завдання 39

Перевірити баланс. При необхідності привести до збалансованого вигляду за рахунок штучного введення постачальника a_i, або споживача b_jз вартістю виконання перевезень 10. Знайти первісний опорний план транспортної задачі за правилом „північно-західного кута”, та методом мінімального елементу. Розрахувати і порівняти результати. Розв’язати транспортну задачу за методом потенціалів.

	bj ai	100	70	165	90			bj ai	70	130	120	75
	65	7	1	3	8			125	8	7	6	5
	140	5	8	4	1			150	1	8	7	4
	120	7	6	2	3			95	6	3	2	3
	60	5	2	4	2
	40	1	6	5	3

Завдання 40

Перевірити баланс. При необхідності привести до збалансованого вигляду за рахунок штучного введення постачальника a_i, або споживача b_jз вартістю виконання перевезень 10. Знайти первісний опорний план транспортної задачі за правилом „північно-західного кута”, та методом мінімального елементу. Розрахувати і порівняти результати. Розв’язати транспортну задачу за методом потенціалів.

	bj ai	80	60	140	115			bj ai	30	125	105	80
	130	5	6	7	8			145	6	4	3	1
	55	1	3	8	5			90	5	2	2	8
	105	2	1	4	7			60	1	3	7	7
	80	2	3	6	5
	25	4	3	1	2

Завдання 41

Перевірити баланс. При необхідності привести до збалансованого вигляду за рахунок штучного введення постачальника a_i, або споживача b_jз вартістю виконання перевезень 10. Знайти первісний опорний план транспортної задачі за правилом „північно-західного кута”, та методом мінімального елементу. Розрахувати і порівняти результати. Розв’язати транспортну задачу за методом потенціалів.

	bj ai	130	40	155	100			bj ai	90	120	85	60
	50	8	5	6	7			100	3	4	5	6
	90	2	1	3	8			170	2	3	2	7
	105	5	4	1	2			135	1	4	1	8
	70	7	2	3	6
	110	3	4	5	1

Завдання 42

Перевірити баланс. При необхідності привести до збалансованого вигляду за рахунок штучного введення постачальника a_i, або споживача b_jз вартістю виконання перевезень 10. Знайти первісний опорний план транспортної задачі за правилом „північно-західного кута”, та методом мінімального елементу. Розрахувати і порівняти результати. Розв’язати транспортну задачу за методом потенціалів.

	bj ai	105	90	125	130			bj ai	75	85	40	90
	70	1	5	1	3			105	1	3	5	7
	100	4	6	3	7			130	8	6	4	2
	75	5	1	3	5			80	2	4	6	8
	90	4	2	8	8
	115	2	2	7	6

Завдання 43

Перевірити баланс. При необхідності привести до збалансованого вигляду за рахунок штучного введення постачальника a_i, або споживача b_jз вартістю виконання перевезень 10. Знайти первісний опорний план транспортної задачі за правилом „північно-західного кута”, та методом мінімального елементу. Розрахувати і порівняти результати. Розв’язати транспортну задачу за методом потенціалів.

	bj ai	70	90	80	110			bj ai	90	115	85	120
	60	1	2	3	4			75	1	2	7	6
	100	6	5	4	5			110	4	3	8	5
	40	7	4	3	6			150	5	6	7	4
	30	8	3	2	7
	120	1	2	1	8

Завдання 44

Перевірити баланс. При необхідності привести до збалансованого вигляду за рахунок штучного введення постачальника a_i, або споживача b_jз вартістю виконання перевезень 10. Знайти первісний опорний план транспортної задачі за правилом „північно-західного кута”, та методом мінімального елементу. Розрахувати і порівняти результати. Розв’язати транспортну задачу за методом потенціалів.

	bj ai	70	90	80	110			bj ai	90	115	85	120
	60	1	2	3	4			75	1	2	7	6
	100	6	5	4	5			110	4	3	8	5
	40	7	4	3	6			150	5	6	7	4
	30	8	3	2	7
	120	1	2	1	8

Завдання 45

Перевірити баланс. При необхідності привести до збалансованого вигляду за рахунок штучного введення постачальника a_i, або споживача b_jз вартістю виконання перевезень 10. Знайти первісний опорний план транспортної задачі за правилом „північно-західного кута”, та методом мінімального елементу. Розрахувати і порівняти результати. Розв’язати транспортну задачу за методом потенціалів.

	bj ai	100	80	60	150			bj ai	95	110	135	70
	130	1	7	8	1			200	1	7	2	6
	70	6	2	6	2			180	8	1	5	3
	50	1	5	3	5			120	7	4	2	5
	80	5	2	4	4
	60	6	4	3	3

Завдання 46

Перевірити баланс. При необхідності привести до збалансованого вигляду за рахунок штучного введення постачальника a_i, або споживача b_jз вартістю виконання перевезень 10. Знайти первісний опорний план транспортної задачі за правилом „північно-західного кута”, та методом мінімального елементу. Розрахувати і порівняти результати. Розв’язати транспортну задачу за методом потенціалів.

	bj ai	40	80	70	140			bj ai	110	105	70	160
	50	1	2	3	4			85	8	7	6	5
	100	2	1	4	3			120	5	6	7	4
	30	3	8	5	2			140	4	2	8	3
	60	4	7	6	1
	90	5	6	7	8

Завдання 47

Перевірити баланс. При необхідності привести до збалансованого вигляду за рахунок штучного введення постачальника a_i, або споживача b_jз вартістю виконання перевезень 10. Знайти первісний опорний план транспортної задачі за правилом „північно-західного кута”, та методом мінімального елементу. Розрахувати і порівняти результати. Розв’язати транспортну задачу за методом потенціалів.

	bj ai	75	85	40	90			bj ai	100	70	115	90
	65	1	3	5	7			160	1	3	4	6
	30	8	6	4	2			130	2	7	8	1
	60	2	4	6	8			145	5	2	3	8
	80	7	5	3	1
	55	1	3	4	2

Завдання 48

Перевірити баланс. При необхідності привести до збалансованого вигляду за рахунок штучного введення постачальника a_i, або споживача b_jз вартістю виконання перевезень 10. Знайти первісний опорний план транспортної задачі за правилом „північно-західного кута”, та методом мінімального елементу. Розрахувати і порівняти результати. Розв’язати транспортну задачу за методом потенціалів.

	bj ai	130	145	85	60			bj ai	130	95	55	155
	80	3	2	4	1			95	5	1	3	4
	65	2	3	1	5			125	6	2	7	4
	75	3	2	4	4			160	1	5	8	3
	80	1	2	3	4
	120	6	7	8	9

Література.

1. Вітлінський В.В. Моделювання економіки: Навч. Посібник. – К.: КНЕУ, 2003. – 408с.

2. Економіко-математичне моделювання світогосподарських процесів: Навч. посіб. — 3-тє вид., перероб. і доп. Рекомендовано МОН / Голіков А.П. — К., 2009. — 222 с.

3. Данилов Н.Н., Иноземцева Л.П. Основы математической экономики. М.: Изд-во АСА, 2004. 348 с.

4. Колемаев В.А. Экономико-математическое моделирование. Моделирование макроэкономических процессов и систем: учебник для студентов вузов, обучающихся по специальности 061800 «Математические методы в экономике» / В.А.Колемаев. – М.: ЮНИТИ-ДАНА, 2005.-295с.

5. Кігель В. Р. Методи і моделі підтримки прийняття рішень у ринковій економіці: Монографія. — К.: ЦУЛ, 2003. — 202 с.

6. Кігель В. Р. Математичні методи ринкової економіки: Навч. посіб. — К.: Кондор, 2003. — 158 с.

7. Трояновский В. М. Математическое моделирование в ме- неджменте: Учеб. пособие.— 2-е изд., испр. и доп. —М.: Изд-во РДЛ, 2002. — 256 с.

8. Бережная Е. В., Бережной В. И. Математические методы моделирования экономических систем: Учеб. пособие. — М.: Финансы и статистика, 2003. — 368 с.

9. Зайченко Ю.П. Дослідження операцій: підручник вид.7 / Киев: Вид. дім "Слово", 2006. – 816 с.

10. Ульяненко О. В. Дослідження операцій в економіці: Підруч­ник / ХНАУ ім. В. В. Докучаева. — Х.: Гриф, 2002.—570 с.

11. Информационные технологии в бизнесе / Под ред. М.Желены. – СПб: Питер, 2002. –1120с.

12. Математичне програмування. Методичні вказівки, програма та контрольні завдання для самостійної роботи студентів економічних спеціальностей / Укл.: В.В. Гончаров, С.Я. Гончарова – Кіровоград: КДТУ, 2004 р. – 136 с.